It might not be immediately obvious why, in a closed population with the same number of men and women, the average number of sexual partners for men must equal the average number of sexual partners for women. Here's a proof.

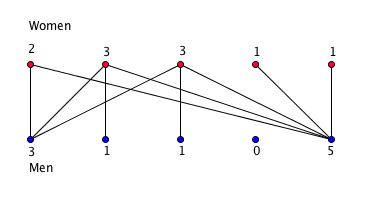
Suppose there are $n$ men and $n$ women and imagine lining them up in two rows, the women facing the men. Now draw a line between a man and a woman if they have been sexual partners. The number of lines emanating from a woman is the number of sexual partners she has had. Therefore, the total number $w$ of lines emanating from the women ($w=10$ in the picture) divided by the total number $n$ of women in the population gives you the average number of sexual partners per woman (which is $10/5=2$ in the picture). By the same argument, the total number $m$ of lines emanating from the men divided by the total number $n$ of men in the population gives you the average number of sexual partners per man. But since each line that emanates from a woman connects to a man, we have $w=m.$ Therefore, we have $$w/n=m/n,$$ so the two averages are equal.

Back to the main article