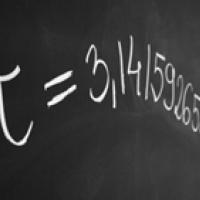
Celebrating a new pi record!

This week a team from the University of Graubünden in Switzerland announced that they have calculated the decimal digits of the number $\pi$ to a record 62.8 trillion places. The calculation took 108 days and 9 hours, making it over three times faster than the calculation that gave us the last record, which had calculated the digits of $\pi$ to a mere 50 trillion places.

The number $\pi$ is what you get when you divide a circle's circumference by its diameter and is the same for any circle, no matter how big or small. The number is irrational, which means it can't be written as a fraction. It also means that its decimal expansion is infinitely long and doesn't end in repeating blocks. It would be impossible to write down the entire decimal expansion of $\pi$ (you'd need an infinite amount of time and an infinite piece of paper). All we can ever hope to do is calculate a finite piece of it, giving us an approximation of $\pi$ — the more decimal places, the more accurate the approximation.

Because $\pi$ lies at the heart of any technology involving rotation or waves, it has many uses outside of maths. You need it to construct rotating parts in jet engines, for example, or the rings used in medical imaging devices like CAT or MRI scanners, and for frequency calculations for mobile phone and GPS devices (find out more in this article).

Many of these uses of the number $\pi$ require you to know its value to a high degree of accuracy, but that's not the reason why the Swiss team, and most other $\pi$ record hunters out there, go to the effort they do. The latest record was achieved by a team from the Centre for Data Analytics, Visualization and Simulation (DAViS) at Graubünden, who wanted to test and show off their computing expertise. "Our attempt at the record had several aims," said Heiko Rölke, Head of DAViS. "In the course of the preparation and execution of the calculations we built up a lot of know-how and optimised our processes. This is particularly useful for our research groups with whom we are working on computing intensive projects in data analysis and simulation."

Computers can perform the calculations a lot faster than any human could ever hope to, but at the heart of those calculations lie mathematical formulas you could, in theory at least, work out with pencil and paper. There are various mathematical algorithms that allow you to calculate the value of $\pi$ to any degree of accuracy if only you execute sufficiently many steps of the algorithm.

A relatively simple one comes from the infinitely long sum \begin{equation} 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} + \ldots $$\end{equation} The more terms in this sum you add (or subtract), the closer the result to the value of $\pi/4$. In fact, by adding sufficiently many terms you can get as close as you like to the value of $\pi/4$. You then only need to multiply your result by $4$ to get an approximation of $\pi$.

The problem with using our expression (1) is that you need to include a large number of terms to get a decent degree of accuracy. If you include 100 terms and multiply the result by $4$, you get $3.146567747182956$. This is fairly close to $\pi=3.141592653589793...$ but it's not a particularly accurate estimate given the effort involved in adding up 100 terms.

The DAViS team used an algorithm based on a more complex looking sum, which was published in 1988 by the Chudnovsky brothers. The sum is written as $$\frac{1}{\pi} = 12 \sum_{q=0}^{\infty} \frac{(-1)^q(6q)!(545140134q+13591409)}{(3q)!(q!)^3(640320)^{3q+3/2}}.$$ The symbol $\sum$ tells us that we are dealing with a sum in which each term has the form that comes after the $\sum$ symbol. The $q=0$ at the bottom of the $\sum$ means that for the first term in the sum you substitute $q=0$ in the expression after $\sum$, for the second term in the sum you substitute $q=1$ in the expression after $\sum$, for the third term in the sum you substitute $q=2$ in the expression after $\sum$, and so on. The infinity sign on top of the $\sum$ symbol means that you keep substituting values of $q$ forever, all the way up to infinity. For any $q$, the expression $q!$ stands for $$q! = q \times (q-1) \times (q-2) \times (q-3) \times ... \times 2 \times 1.$$ The more terms of this sum you add up, the closer the result to $1/\pi.$ You now only need to divide $1$ by your result to get an approximation for $\pi$. The Chudnovsky algorithm is the most efficient method that is know for calculating the decimal places of $\pi$.

For more on how to approximate $\pi$ using infinite sums, see our article How to add up quickly by Chris Budd.

For the record, the last ten digits in the known part of the decimal expansion of $\pi$ are $7817924264$. Congratulations to the DAViS team!