Bored at work but have little desk space? Then maybe the new quantum version of the classic executive desk toy, Newton's cradle, is for you. While away the hours watching the hundreds of atoms banging back and forth, back and forth... And even better than the original version, the quantum one just keeps going — even after thousands of collisions!

The classical Newton's cradle involves a number of steel balls, usually five, suspended in a line by fine wires. If you set one ball swinging it hits the stationary balls and its momentum is transferred through each of them until exactly one ball at the opposite end swings away, the rest remaining stationary (you can see a video of this motion at the Penn State site). It is a good demonstration of conservation of momentum, but the energy in the system is dissipated through damping effects such as friction and the movement eventually slows down. (You can read more about the maths behind Newton's cradle from Egglescliffe School and School for champions.)

A classical Newton's cradle
(Image: Penn State Campus Photography, Frederic Weber)

Physicists from Penn State University have constructed a quantum version of Newton's cradle and became the first people to observe a system with many colliding particles whose motion doesn't become chaotic. Using lasers to build tube shaped traps, they forced atoms to move only in one dimension. They loaded the traps with about 150 atoms that were chilled to extremely low temperatures, just billionths of a degree above absolute zero. Other laser beams set the atoms in motion, half of the atoms moving to the left and half to the right, these groups then oscillated in the trap in a very similar way to the balls in a Newton's cradle. (Watch a video of this type of movement, demonstated with a classical Newton's cradle.)

"The quantum Newton's cradle is just like a classical Newton's cradle, exept that it's more perfectly one dimensional and instead of 5 balls there are hundreds," says David Weiss, leader of the research team. "Also, because it's a quantum system, the atoms often just go right through each other, which never happens with the executive desk toy. Another difference is that you can't buy the quantum Newton's cradle on the Internet."

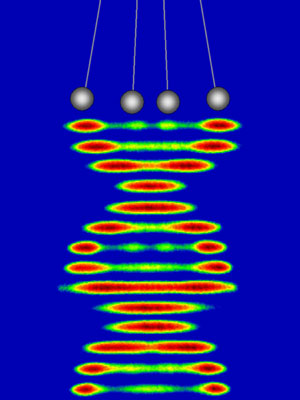
Images of quantum Newton's cradles during their first cycle of oscillation. Each atom collides with half the other atoms twice each 13 ms cycle, sometimes bouncing off each other, sometimes passing through each other. The cartoon steel balls drawn at the top show the analogy between the quantum and classical Newton's cradle.
(Image: David Weiss, Penn State)

But the most exciting difference was that even after thousands of collisions, the movement of the atoms stayed the same. "A fascinating thing about this system is the remarkable stability of its momentum profile, which does not change even after each atom in the system has collided thousands of times," says Weiss. The movement of the particles never became chaotic. "We set all the atoms oscillating in the trap with almost the same aplitude. We found that even after each atom has bounced of the other atoms 10,000 times, each still oscilates with the original amplitude."

Usually the motion of many particle systems, such as gases, eventually becomes chaotic, reaching a state physicists call thermal equilibrium. In this state all the parameters describing the system, such as temperature, are unchanging. However the system that Weiss and his team created never reaches this state, and instead a constant predictable motion was maintained by the atoms. The theoretical understanding about this type of system predicted that this non-chaotic behaviour was possible, but the researchers were the first people to ever witness it.

Weiss says that the absence of chaotic behaviour in the system can be explained by the fact the equations of motion for the system precisely dictate how it evolves in time. Physical systems are usually too complex for this to happen, too many interacting factors mean that the equations describing the motion of their particles cannot be solved. But the equations of motion for the system Weiss and his team constructed can be solved to predict where each particle will be at any time in the future or where it was at any time in the past — such a system is called integrable. (You can read more about integrable systems in the Plus article "Lagrange and the Interplanetary Superhighway".)

"The equations of motion dictate how the system evolves in time," says Weiss. The equations for the quantum Newton's cradle account for the kinetic energy of the particles, the collisions among the particles and the way they are confined to one dimension. The system they created is nearly fully integrable, explaining the unchanging nature of the atoms motion even after thousands of collions: "The last three terms in the equations of motion compromise the integrability, but apparently not enough to let our system [move towards thermal equilbrium] for a very long time." Weiss says that the classical Newton's cradle is close to integrable, but complications, such as the inelasticity of the collisions, violate the integrability. "But the prominent behaviour of the Newton's cradle, where N balls coming in makes N balls come out, contains the essence of the near-integrability of the system. It is also a good description of what happens in our experimental system, which has many more particles and is much closer to fully integrable."

"Only a handfull of integrable many-body systems are known, and this is the first time that any of them has been observed experimentally," Weiss says. Now that such a system can be studied in the lab, the researchers hope to understand exactly how to tip it into chaos. They propose making the system less one dimensional, by allowing some some of the atoms to tunnel between the tube shaped traps, gradually changing the system from one with collisions in one dimension, to a system with collisions in two or three dimensions. "The system's integrability can thus be comprimised in a controlled way, presenting a new type of experimental model for the onset of chaos," the researchers wrote in their recent paper in Nature.

The research may lead to new understanding of the boundary between order and chaos in physical systems. Weiss and his team have created a physical system that has only previously been studied theoretically, offering the opportunity to finally study and test those theories in real life experiments. "Theory has guided experiments up to now, but experiments are now in a position to guide the theory," says Weiss. "It's a fine example of the way scientific progress is made."