
Chaotic crochet
If you find yourself with some spare time over the Christmas break, why not try your hand at crocheting some chaos? And no, we don't mean ending up in a tangled mess, but instead crocheting the beautiful Lorenz manifold, instructions for which are published in the current issue of the journal Mathematical Intelligencer.
In 1963 the meteorologist Ed Lorenz studied a basic model for the weather, and discovered the Butterfly Effect, illustrated by the idea of a butterfly flapping its wings in America today causing hurricanes a week later in Europe. This is because the weather, and the Lorenz equations modelling it, are chaotic systems - small changes in initial conditions can produce vastly different results.
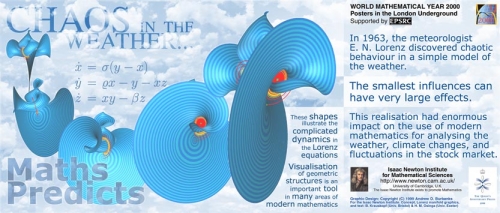
Maths predicts - one of the "Maths on the Tube" posters featuring the Lorenz equations.
Osinga and Krauskopf created the content for the poster, including the beautiful images
of the Lorenz manifold and Lorenz attractor.
The Lorenz equations describe the paths of points in three-dimensional space over time. The famous butterfly-shaped Lorenz attractor - the yellow and red set of points on the images in the poster above - is a one-dimensional spiralling line forming two "wings". Almost all the points in the system are attracted to this spiral, but once on it move chaotically, switching from one loop to another. "In a simple numerical simulation of the Lorenz system on your computer, starting from almost any initial condition, will quickly produce an image of the Lorenz attractor," Mathematicians Hinke Osinga and Bernd Krauskopf, from the Department of Engineering Mathematics at Bristol University, said in their mathematical explanation of the crocheted Lorenz manifold.
However, the Lorenz manifold - the blue surface in the images - is a special collection of points that do not behave this way: "While most trajectories end up at the Lorenz attractor, those on the Lorenz manifold converge to the origin [0] instead". And this special collection of points makes up the two-dimensional surface of the Lorenz manifold that is replicated in the crocheted model. "Imagine a leaf (a point in the system) floating in a turbulent river and consider how it passes either to the left or the right around a rock (the origin) somewhere downstream," says Osinga. "Those special leaves that end up clinging to the rock must have followed a very unique path in the water. Each stitch in the crochet pattern represent a single point that ends up at the rock." (Read more about the Lorenz equations in Maths Predicts, one of the Maths on the Tube posters previously featured on Plus.)
Many mathematicians had already been working on ways of computing the Lorenz manifold, and Osinga and Krauskopf had developed a method for visualising it on a computer. However, there had been no real-life model of the manifold. The pair were inspired to try crocheting a model of the surface when Osinga was relaxing with some crocheting over Christmas 2002 and Krauskopf suggested she crochet something useful!
Their algorithm for representing the manifold on a computer "grows" the surface in steps, by starting from a small disc and adding consecutive bands with points added or removed to reflect the shape of the surface. In this way, the overall shape of the surface is created by little local changes: adding or removing points at each step. (You can see some lovely animations of the manifold on their website.)

Osinga and Krauskopf with their crocheted model of the Lorenz manifold
Osinga has been able to crochet since she was seven years old , so she noticed that this is exactly the same way that crochet instructions work - by specifying a "surface" (more usually a poncho or baby's blanket!) in rows, with the number of stitches increasing or decreasing. From there it was a simple step to turn the algorithm into a crochet pattern, and to start to create a real-life Lorenz manifold. "The computer-generated crochet instructions were remarkable," says Osinga. "Simply by looking at the real-life surface I would never have designed it the way the computer did."
The final product is about one metre wide and took Osinga two months and 25,511 stitches to complete. It is held in shape by three wires (along the vertical axis, around the edge of the model, and following a trajectory that crosses the vertical horizontally at the centre). "After all those months of trying to create it on screen, it was fascinating to see the surface grow under my own hands," says Osinga. Krauskopf adds: "And it was truly amazing to see a floppy object fall into its desired shape when it was mounted with steel wire."
They have since "toured" the first crocheted model and have found that it is a "very helpful tool for understanding and explaining the dynamics of the Lorenz system". Pointing out that while the model is not identical to the computer generated Lorenz manifold, all its geometric features are truthfully represented, and they say the crochet model makes it possible to "convey the intricate structure of this surface in a 'hands-on' fashion."
Osinga has since made a second model, seen in the photo above, that now hangs as an unusual Christmas decoration in their home. Full instructions for crocheting and mounting your own Lorenz manifold is given in their paper, and they are encouraging others to take on the challenge. There is even a bottle of champagne on offer for the first dexterous and mathematically minded person who creates model number three. So why not work off some of that Christmas pudding and get crocheting on chaos!