
Cracking codes
"Few persons can be made to believe that it is not quite an easy thing to invent a method of secret writing which shall baffle investigation. Yet it may be roundly asserted that human ingenuity cannot concoct a cipher which human ingenuity cannot resolve..."
Edgar Alan Poe - "A few words on secret writing"; 1841
Human desire to communicate secretly is at least as old as writing itself and goes back to the beginnings of our civilisation. Methods of secret communication were developed by many ancient societies, including those of Mesopotamia, Egypt, India, China and Japan, but details regarding the origins of cryptology, i.e. the science and art of secure communication, remain unknown.
Classical cryptography

The scytale
We know that it was the Spartans, the most warlike of the Greeks, who pioneered cryptography in Europe. Around 400 BC they employed a device known as the scytale. The device, used for communication between military commanders, consisted of a tapered baton around which was wrapped a spiral strip of parchment or leather containing the message. Words were then written lengthwise along the baton, one letter on each revolution of the strip. When unwrapped, the letters of the message appeared scrambled and the parchment was sent on its way. The receiver wrapped the parchment around another baton of the same shape and the original message reappeared.
In his correspondence, Julius Caesar allegedly used a simple letter substitution method. Each letter of Caesar's message was replaced by the letter that followed it alphabetically by three places. The letter A was replaced by D, the letter B by E, and so on. For example, the English word COLD after the Caesar substitution appears as FROG. This method is still called the Caesar cipher, regardless the size of the shift used for the substitution.
Simple substitution ciphers are easy to break. For example, the Caesar cipher with 25 letters admits any shift between 1 and 25, so it has 25 possible substitutions (or 26 if you allow the zero shift). One can easily try them all, one by one. The most general form of one-to-one substitution, not restricted to the shifts, can generate
26! or 403,291,461,126,605, 635,584,000,000
possible substitutions. And yet, ciphers based on one-to-one substitutions, also known as monoalphabetic ciphers, can be easily broken by frequency analysis. The method was proposed by the 9th century polymath from Baghdad, al-Kindi (800-873AD), often called the philosopher of the Arabs.

Al-Kindi noticed that if a letter in a message is replaced with a different letter or symbol then the new letter will take on all the characteristics of the original one. A simple substitution cipher cannot disguise certain features of the message, such as the relative frequencies of the different characters. Take the English language: the letter E is the most common letter, accounting for 12.7% of all letters, followed by T (9.0%), then A (8.2%) and so on. This means that if E is replaced by a symbol X, then X will account for roughly 13% of symbols in the concealed message, thus one can work out that X actually represents E. Then we look for the second most frequent character in the concealed message and identify it with the letter T, and so on. If the concealed message is sufficiently long then it is possible to reveal its content simply by analysing the frequency of the characters.
Renaissance cryptography

In the fifteenth and the sixteenth centuries, monoalphabetic ciphers were gradually replaced by more sophisticated methods. At the time Europe, Italy in particular, was a place of turmoils, intrigues and struggles for political and financial power, and the cloak-and-dagger atmosphere was ideal for cryptography to flourish.
In the 1460s Leone Battista Alberti (1404-1472), better known as the Renaissance architect, invented a device based on two concentric discs that simplified the use of Caesar ciphers. The substitution - i.e. the relative shift of the two alphabets - is determined by the relative rotation of the two disks.
Rumour has it that Alberti also considered changing the substitution within one message by turning the inner disc in his device. It is believed that this is how he discovered the so-called polyalphabetic ciphers, which are based on superpositions of Caesar ciphers with different shifts. For example, the first letter in the message can be shifted by 7, the second letter by 14, the third by 19, the fourth again by 7, the fifth by 14, the sixth by 19, and so on repeating the shifts 7, 14, 19 throughout the whole message. The sequence of numbers - in this example 7, 14, 19 - is usually referred to as a cryptographic key. Using this particular key we transform the message SELL into its concealed version, which reads ZSES.
In technical terms the message to be concealed is often called the plaintext and the operation of disguising it is known as encryption. The encrypted plaintext is called the ciphertext or cryptogram. Our example illustrates the departure from a simple substitution; the repeated L in the plaintext SELL is enciphered differently in each case. Similarly, the repeated S in the ciphertext represent a different letter in the plaintext: the first S corresponds to the letter E and the second to the letter L. This makes the straightforward frequency analysis of characters in ciphertexts obsolete. Indeed, polyalphabetic ciphers invented by the main contributors to the field at the time, such as Johannes Trithemius (1462-1516), Blaise de Vigenere (1523-1596), and Giovanni Battista Della Porta (1535-1615), were considered unbreakable for at least another 200 years.
(Not so) unbreakable
The first description of a systematic method of breaking polyalphabetic ciphers was published in 1863 by the Prussian colonel Friedrich Wilhelm Kasiski (1805-1881), but, according to some sources (for example, Simon Singh, The code book), Charles Babbage (1791-1871) had worked out the same method in private sometime in the 1850s.
The basic idea of breaking polyalphabetic ciphers is based on the observation that if we use N different substitutions in a periodic fashion then every Nth character in the cryptogram is enciphered with the same monoalphabetic cipher. In this case we have to find N, the length of the key, and apply frequency analysis to sub-cryptograms composed of every Nth character of the cryptogram.
But how do we find N? We look for repeated sequences in the ciphertext. If a sequence of letters in the plaintext is repeated at a distance which is a multiple of N, then the corresponding ciphertext sequence is also repeated. For example, for N=3, with the 7, 14, 19 shifts we encipher
TOBEORNOTTOBE
as
ACULCVUCMACUL:
| T | O | B | E | O | R | N | O | T | T | O | B | E |
| A | C | U | L | C | V | U | C | M | A | C | U | L |
The repeated sequence ACUL is a giveaway. The repetition appears at a distance 9 thus we can infer that possible values of N are 9 or 3 or 1. We can then apply frequency analysis to the whole cryptogram, to every third character and to every ninth character; one of them will reveal the plaintext. This trial and error approach is getting more difficult for large values of N, i.e. for very long keys.
In the 1920s electromechanical technology transformed the original Alberti's disks into rotor machines in which an encrypting sequence with an extremely long period of substitutions could be generated, by rotating a sequence of rotors. Probably the most famous of them is the Enigma machine, patented by Arthur Scherbius in 1918. (See Claire Ellis's article about the Enigma and its role in the Second World War, also in this issue of Plus.)
A notable achievement of cryptanalysis was the breaking of the Enigma in 1933. In the winter of 1932, Marian Rejewski, a twenty-seven year old cryptanalyst working in the Cipher Bureau of the Polish Intelligence Service in Warsaw, mathematically determined the wiring of the Enigma's first rotor. From then on, Poland was able to read thousands of German messages encrypted by the Enigma machine. In July 1939 Poles passed the Enigma secret to French and British cryptanalysts. After Hitler invaded Poland and France the effort of breaking Enigma ciphers continued at Bletchley Park in England. A large Victorian mansion in the centre of the park (now a museum) housed the Government Code and Cypher School and was the scene of many spectacular advances in modern cryptanalysis.
Truly unbreakable?

Claude Shannon
Despite its long history, cryptography only became part of mathematics and information theory in the late 1940s, mainly as a result of the work of Claude Shannon (1916-2001) of Bell Laboratories in New Jersey. Shannon showed that truly unbreakable ciphers do exist and, in fact, they had been known for over 30 years. They were devised in about 1918 by an American Telephone and Telegraph engineer Gilbert Vernam and Major Joseph Mauborgne of the US Army Signal Corps, and are called either one-time pads or Vernam ciphers.
Both the original design and the modern version of one-time pads are based on the binary alphabet. The message, or plaintext, is converted to a sequence of 0's and 1's, using some publicly known rule. The key is another sequence of 0's and 1's of the same length. Each bit of the message, or the plaintext, is then combined with the respective bit of the key, according to the rules of addition in base 2:
0+0=0,
0+1=1+0=1,
1+1=0.
The key is a random sequence of 0's and 1's, and therefore the resulting cryptogram - the plaintext plus the key - is also random and completely scrambled unless one knows the key. The plaintext can be recovered by adding (in base 2 again) the cryptogram and the key.
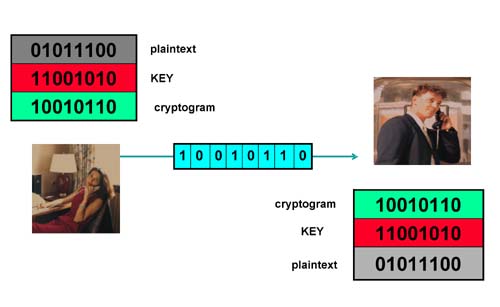
In the example above, the sender, traditionally called Alice, adds each bit of the plaintext (01011100) to the corresponding bit of the key (11001010) obtaining the cryptogram (10010110), which is then transmitted to the receiver, traditionally called Bob. Both Alice and Bob must have exact copies of the key beforehand; Alice needs the key to encrypt the plaintext, Bob needs the key to recover the plaintext from the cryptogram. An eavesdropper, called Eve, who has intercepted the cryptogram and knows the general method of encryption but not the key, will not be able to infer anything useful about the original message. Indeed, Shannon proved that if the key is secret, the same length as the message, truly random, and never reused, then the one-time pad is unbreakable. Thus we do have unbreakable ciphers!

How to distribute them?
There is, however, a snag. All one-time pads suffer from a serious practical drawback, known as the key distribution problem. Potential users have to agree secretly and in advance on the key - a long, random sequence of 0's and 1's. Once they have done this they can use the key for enciphering and deciphering, and the resulting cryptograms can be transmitted publicly, for example, broadcasted by radio, posted on Internet or printed in a newspaper, without compromising the security of messages. But the key itself must be established between the sender and the receiver by means of a very secure channel - for example, a very secure telephone line, a private meeting or hand-delivery by a trusted courier.
Such a secure channel is usually available only at certain times and under certain circumstances. So users far apart, in order to guarantee perfect security of subsequent crypto-communication, have to carry around with them an enormous amount of secret and meaningless information (cryptographic keys), equal in volume to all the messages they might later wish to send. This is, to say the least, not very convenient!
Furthermore, even if a "secure" channel is available, this security can never be truly guaranteed. A fundamental problem remains because, in principle, any classical private channel can be monitored passively, without the sender or receiver knowing that the eavesdropping has taken place. This is because classical physics - the theory of ordinary-scale bodies and phenomena such as paper documents, magnetic tapes and radio signals - allows all physical properties of an object to be measured without disturbing those properties. Since all information, including cryptographic keys, is encoded in measurable physical properties of some object or signal, classical theory leaves open the possibility of passive eavesdropping, because in principle it allows the eavesdropper to measure physical properties without disturbing them. This is not the case in quantum theory, which forms the basis for quantum cryptography.
We continue the story in the next issue of Plus.
About the author
Artur Ekert splits his time between the University of Cambridge, where he is a Professor of Quantum Physics at DAMTP and a Professorial Fellow of King's College, and the National University of Singapore, where he is a Distinguished Professor. He is one of the discoverers of quantum cryptography.
Comments
Hi
Your writing is really good. It’s hard for me to focus, but without realizing I read through everything and it was easy to understand
ricky
this is fab i am a teacher and i was doing a cover lesson and i had a look and it helped me