Have you ever played pooh sticks? You and your rival find a stick each; you line up on one side of the bridge, count "3, 2, 1, GO!", then drop your sticks into the stream below. You dash to the other side of the bridge and peer frantically into the water to see whose stick will appear first.

Sometimes you are lucky and your stick whooshes through, carried by fast-flowing water. Sometimes your stick will get stuck in reeds or against the bridge supports. And sometimes, especially if you dropped it near the bank, your stick will do something very bizarre and go round and round in circles. If you are unlucky enough to experience the last scenario while your younger brother's stick moves as if it's jet propelled (no, I'm not bitter), it will probably be of little consolation to know that your stick has got stuck in an eddy.

Throwing floating objects into water to understand how the currents move is no new idea. Oceanographers have been following with interest the progress of an escaped cargo of rubber ducks[1], and another of Nike trainers[2], that have been circumnavigating the globe. Satellite images of these floating markers can provide information about ocean currents. These markers are also blown along by the wind as they sit on the water surface.

The great mathematician Sir James Lighthill[3,4] used to use his extensive understanding of how fluids behave to help him swim around the island of Sark in the Channel Islands. He did his homework on the local tides and currents, and his understanding of the flow allowed him to use these currents to his advantage to help carry him around the island. At the age of 49, Lighthill was the first person to complete the 9 mile trip around the island saying that it was "a most pleasant way to see the scenery". Sadly, he died during an attempt to repeat this tremendous feat, aged 74, and in extremely stormy conditions.

Part of my PhD project has been to measure the coastal currents in and around a particular bay on the Devon coastline called Blackpool Sands. My colleagues at the Brixham Environmental Laboratory and I joked about throwing oranges or turnips into the water, then standing atop the cliffs to record with a camera how the currents moved these markers around. However, the beach is privately owned and a popular spot with holiday-makers (who probably wouldn't have been impressed if they'd suddenly been surrounded by turnips) so we had to be careful to avoid swimmers as we pottered around the bay in a boat. We used an instrument called an acoustic Doppler current profiler. This was hung off the side of the boat and used to measure the flow velocities. It emits pings and listens for echoes bouncing back from small particles in the water. The pitch of the echo varies depending on the speed and direction of the particles, just as the pitch of an ambulance siren changes as it whizzes past you (except we can't hear the instrument's pings).

A bird's eye view of Blackpool Sands in Devon

I went to chat to the beach life-guard to explain what we were doing: investigating the coastal sea currents to try to predict where pollution might go. "And bodies!" he suggested. I was appalled; and yet horribly fascinated. Some internet research revealed a story about an Ontario fireman who tracked the bodies of people who had fallen into rivers[5]. He threw a bag of bran into the water at the person's point of entry, and followed the floating bran as it led him to the casualty. Of course, being able to predict where a casualty might float would be useful for the rescuers, who might then be able to anticipate the path of, and therefore catch up with, the casualty, rather than have to wait until the person came to rest. This prediction of the currents could usefully be attempted using a computer model, and indeed it has: a paper published in the Journal of Forensic Science describes the use of a coastal current computer model to predict the course of casualties[6].

Computer models of water currents can also be used to predict the fate of pollutants released into the water. We need to know where the pollutant is likely to go, and how dilute, or spread out, it is likely to get. For an accidental pollutant release, such as an oil tanker spill, this is important for cleanup operations. If the pollutant is going to dilute very quickly, it may not be possible to clean it up, but then, in a very dilute form, it may not have a dangerous impact on the environment. However, if a pollutant is likely to remain in a very concentrated patch, it will be easier to contain, and perhaps to clean up. For such a concentrated spill, cleanup may be extremely urgent if the pollutant is at dangerous levels for the environment.

For a controlled release of pollutant, such as a sewage out-fall pipe, predicting the pollutant's fate will be important for designing the pipe length (how far must it be released from the shore?) and how fast the pollutant may be released without damaging the environment. At the Brixham Environmental Laboratory, modellers use complex computer codes to predict the path of pollutant releases. For example, factories on estuary or river banks need to have contingency plans, so that they know exactly what to do in case of accidental pollutant release. To formulate these plans they need to know what is likely to happen to a pollutant release. You can see an example of their modelling at http://www.brixham-lab.com/Article/509226.aspx.

As the sea level rises the water covers more of the beach

Returning to Blackpool Sands, the currents outside the bay were already known because the Admiralty produce maps to tell sailors about the currents and sea depths. We often think of tides flowing in and out, but this is the effect of the water levels changing. For example, as the sea level rises, water covers more of the beach and therefore "comes in". However, the tidal currents offshore near Blackpool Sands actually flow back and forth along the coast (this is typical of tidal currents in a channel (tides in some places rotate through 360^o instead).

The tidal currents at Blackpool Sands flow across the mouth of the bay, and can be approximated as a sine wave: $$ U = U_0 \sin (\frac{2 \pi t}{T})$$ where U is the speed of the currents, U₀ is the maximum speed of the currents, T is the tidal period which is around 12 hours and 25 minutes, and t is the time since the start of the tidal cycle.

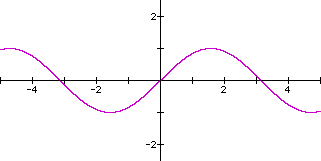
Another sort of wave

This means that the currents are speeding up, slowing down, then changing direction, speeding up and slowing down, and changing direction again, in one tidal cycle. High tide, when the water level is at its highest, and low tide, when the water level is at its lowest, occur roughly when the tide changes direction.

We discovered from our measurements of the flow that an eddy exists in Blackpool Sands bay. When the tidal currents are moving slowly, they enter the bay and appear to cling to the coastline. However, as they speed up, an eddy is created which grows to fill the bay. The tidal currents across the bay mouth are effectively pushing the water in the bay round in a large circle. However, when the tide slows and changes direction, the tidal currents again enter the bay and push the eddy out to sea. A new eddy is then generated as the tide accelerates.

Things can get stuck in this eddy (think of our hapless pooh stick). Imagine if someone decided to build a sewage out-fall pipe just up the coast from the bay: when the tide was in the right (or should that be "wrong"?) direction. If the pipe wasn't built far enough out to sea, sewage might be swept into the eddy and get stuck there until the tide changed direction. That's over six hours of sewage building up. Worse than the turnips, I reckon.

[1] http://news.bbc.co.uk/1/hi/world/americas/3060579.stm

[2] https://news.nationalgeographic.com/news/2001/06/0619_seacargo.html

[3] Crighton, D. G. and Pedley, T. J. 1999 Michael James Lighthill (1924-1998). Notices of the AMS, 46 (10): 1226-1229.

[4] Obituary of Sir James Lighthill (1924-1998), The Times, July 1998. http://www.aam314.vzz.net/Lighthill.html

[5] http://tradersbend.com/lnl/Newsletters/LNLV4N2.html

[6] Ebbesmeyer, C. C. and Haglund, W. D. 1994 Drift trajectories of a floating human-body simulated in a hydraulic model of Puget-Sound. Journal of Forensic Sciences, 39 (1): 231-240.

About the author

Frances Elwell has just completed her PhD at the University of Cambridge. She would like to thank staff at the Brixham Environmental Laboratory for all their help during her PhD, and also Sir Geoffrey Newman, owner of Blackpool Sands, for his support for the fieldwork.

A rather shorter version of this article won Frances a runner-up prize in the New Scientist/Wellcome Trust essay competition 2004.