Graphical methods I: Slug wars
Proof that f(y) is acceleratingly increasing and g(x) is deceleratingly increasing
First, draw yourself a graph to show that only acceleratingly increasing curves starting from a point x0 (which is strictly greater than zero) have the following property:
the curve x=f(y) crosses the line y=rx.
Why is this so? The equation y=rx defines a straight line starting at (0,0). The larger the number r, the steeper the line. An increasing curve f(y) as in our example starts off below the straight line y=rx. If it is to meet this straight line, its steepness has to become greater than that of the line, otherwise it will never catch up. So if it is to meet every line of the form y=rx then it has to reach every possible degree of steepness. It gets steeper and steeper all the time, and this is exactly what acceleratingly increasing means. The point at which they cross may be a long way off the top and side of your piece of paper, but it should be clear that only the acceleratingly increasing curves have this property for every r>0. (Note that the straight line and the deceleratingly increasing curve have this property for some r>0, but not for every r>0.) We will now argue that the curves in the ICSM problem also have this property, and so must be acceleratingly increasing, like the green line in figure 2.
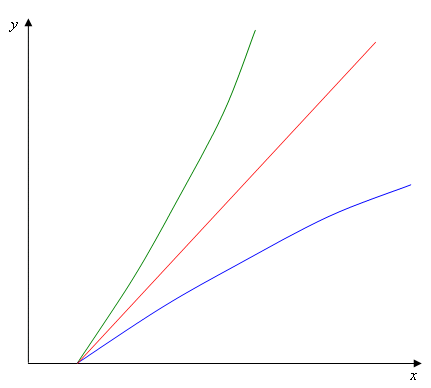
Figure 2: The green acceleratingly increasing curve gets steeper as y increases,
while the steepness of the blue deceleratingly increasing curve decreases.
Our strategy for doing so is to show that for every number r, no matter how large, we can find a point (xr, yr) which lies on the line y=rx, so that SSA feels safe. In other words, SSA believes that if it has xr ICSMs and SSB has yr, then even after a sneak attack by SSB, it has enough left to inflict unacceptable damage on SSB. (You can see that there are a lot of things like "believing", and also somehow knowing what will be "unacceptable" to another country, but that's slug politics for you.)
If we can show this, then we have proved that f(y) is acceleratingly increasing: from the definition of if and only if, we know that SSA feels safe precisely when x>f(y). So the point (xr, yr) lies to the right of f(y). But the line y=rx started on the left of f(y), so the two must have crossed at some point whose first coordinate is smaller than xr. This is true for all values r>0, and so, as we've argued above, f(y) must be an acceleratingly increasing curve.
Some statistics
As explained above, each missile has probability p(r) to survive a sneak attack. We can associate to each missile a random variable which takes the value 0 if that particular missile gets wiped out in the attack and the value 1 if it survives. The value we expect the random variable to take on average is p(r). Mathematicians call this value the expectation of the random variable.
To find the total number of missiles we can expect to survive a sneak attack, we define a new random variable which is simply the sum of the random variables of all the individual missiles. The expectation of the sum of several random variables is equal to the sum of the individual expectations. So, since we have x missiles in total, and the expectation for each is p(r), we expect xp(r) of them to survive.
To start the proof, look at the straight line y=rx. This represents all the situations in which SSB has exactly r times as many weapons as SSA. To wipe out the most ICSMs in a sneak attack, SSB should aim roughly r ICSMs at every SSA missile. But what about those missiles that don't work properly, or spill their salt just off-target? There must be a probability, p(r)>0, that a given ICSM belonging to SSA will survive a sneak attack because of faulty equipment or targeting by SSB.
Borrowing a result from statistics (see the box below), we can say that SSA can expect xp(r) of its ICSMs to survive. Now we can be sure that for large enough x, xp(r) will be bigger than x0 by an amount large enough to cancel any uncertainties (x0 is the starting point of the graph — the number of weapons SSA needs to destroy an acceptable amount of an unarmed SSB). That is, if the slugs of SSA want an extra 10% of their minimal arsenal in hand, they want xp(r)=1.1x0. So at the point (xr,yr), given by xr = 1.1x0/p(r) and yr = rxr, SSA feels safe. And since this point lies on the line y=rx, this is the end of the proof.
Now we can use a very useful tool known as symmetry to say that whatever is true from SSA's viewpoint must also be true from SSB's. If you follow the analysis through, you will see that the curve y=g(x) must be deceleratingly increasing, and so we have confirmed the general form of the graph drawn in figure 1.