"Please hold the line, your call is important to us." It's a sentence we're all frustratingly familiar with. Just as familiar as we are with standing in line at the supermarket or post office, with the other queues seeming to move much faster than the one we happen to be in.

Queueing is boring but maths can help.

Thankfully, mathematics can help. Queueing theory studies such situations mathematically, and tries to find solutions that minimise the average customer waiting time while also limiting the average time a queue server remains idle. This double constraint makes the problem a difficult one. An additional source of difficulty is the randomness involved. Customers usually do not arrive at regular intervals, but their arrival times are what is called a stochastic process. Coming up with a general formula that provides a solution for such stochastic problems is generally difficult, and sometimes even impossible.

Recently my uncle Arie Hordijk and I, together with Bernd Heidergott of VU University Amsterdam, studied such a queueing problem. It often occurs in call centres, where incoming callers have to be assigned to one of several waiting queues that are, for example, distributed over different locations. The particular problem we studied does not have any known analytical solution — that is, there isn't a general mathematical formula for solving it. We considered a worst-case scenario where there is no information available about the current state of the system, such as how long each customer has already been waiting in their respective queue. In practical situations there may be some such information available, but often this information is incomplete, or there is a significant delay in updating it (especially in distributed centres). So, assuming no information at all is a useful starting point from a mathematical point of view.

In such a situation it might seem that the best strategy is to simply assign arriving customers to the available waiting queues at random. This is indeed the standard solution that is used in these cases. What we have now shown, though, is that by using a deterministic assignment strategy (that is, following a pre-determined rule), rather than a random one, the average customer waiting time can actually be reduced significantly. This might seem counterintuitive, given that the system itself behaves stochastically. However, by using a particular customer assignment strategy based on so-called billiard sequences, it is possible to improve on the standard random assignments.

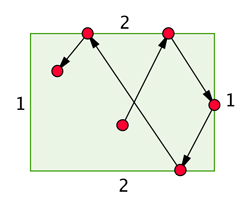
A ball moving on a billiard table. The corresponding billiard sequence starts 2122.

Imagine a billiard table with only one ball on it and no pockets. Also assume that the ball doesn't experience any friction. Now hit the ball (in a given direction), and write down a 1 every time the ball hits one of the two shorter sides of the table, and a 2 every time it hits one of the longer sides of the table. Since there is no friction, the ball will continue moving, giving rise to a long sequence of 1s and 2s. A sequence constructed in this (deterministic) way is called a billiard sequence. Changing the (relative) lengths of the sides of the table, or simply choosing a different direction for the initial hit, results in a different billiard sequence. (Note that we don't need a real billiard table to come up with a billiard sequence: we can calculate it using the starting position and direction of the ball and the law of reflection.)

Mathematically the same procedure can be followed for billiard tables of more than two dimensions. A three-dimensional billiard table is essentially a box which has the ball bouncing around inside it. We assume there's no gravity, so the ball doesn't simply fall down, but continues bouncing between the sides of the box. There are three pairs of opposite sides and we can label these pairs by the numbers 1, 2 and 3. The moving ball now generates a sequence made up of 1s, 2s and 3s. Although we cannot visualise it, we can mathematically define an n-dimensional box, and thus generate a billiard sequence made up of the numbers 1 up to n.

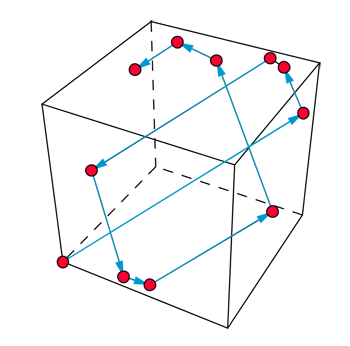
A ball moving in a 3D billiard table, which in this example happens to be a cube. If you label the top and bottom faces with a 1, the front and back faces with a 2, and the other two faces with a 3, the trajectory of the ball defines a billiard sequence.

A customer assignment strategy based on a billiard sequence now simply assigns each next incoming customer to the waiting queue indicated by the next number in this billiard sequence.

We performed computer simulations of a (stochastic) customer arrival system with ten (n=10) available waiting queues, using either a purely random customer assignment strategy, or one based on a billiard sequence. These simulations clearly show that with an appropriate billiard sequence, the average customer waiting time can actually be greatly reduced. (We performed a statistical analysis to make sure the better waiting times weren't just a fluke.)

The main problem, though, is to find such an appropriate billiard sequence (i.e. appropriate relative lengths of the sides of the billiard table). For this, we used a genetic algorithm, a computer program that mimics natural evolution, literally evolving better and better solutions to a given problem. Using this computational method, we were able to find billiard sequences that sometimes even cut the average customer waiting time in half compared to the standard random assignments.

We then also considered additional constraints, such as a fair distribution of the workload over the ten queue servers, or allowing only billiard sequences consisting of a relatively short (but repeated) subsequence. In those cases it is also possible to find (using the genetic algorithm) appropriate billiard sequences that significantly reduce the average customer waiting time compared to random assignments.

These surprising but very useful results, which officially represent my uncle Arie Hordijk's final scientific contribution, were published in a joint article in the Asia-Pacific Journal of Operational Research. With more than 170 publications, five books, and a special issue of the scientific journal Mathematical Methods of Operations Research dedicated to him for his 65th birthday, my uncle is a well-known mathematician. It is a great honor to be a co-author on what will be his very last scientific publication.

Our result clearly shows how a simple idea based on a popular game, when used in an appropriate mathematical setting, can provide solutions to problems we are faced with on a daily basis. Moreover, it is a wonderful example of the power of interdisciplinary collaborations. Combining the theoretical knowledge of two mathematicians with the practical expertise of a computer scientist has led to a significantly improved solution for a difficult problem in queueing theory. And not some hard-to-understand theoretical solution, but one that can be easily implemented in practice too. After all, your call really is important to us!

About the author

Wim Hordijk is a computer scientist currently on a fellowship at the Konrad Lorenz Institute in Klosterneuburg, Austria. He has worked on many research and computing projects all over the world, mostly focusing on questions related to evolution and the origin of life. More information about his research can be found on his website.