
An infinite series of surprises
Introduction
An infinite sum of the form
$$ \begin{equation} a_1 + a_2 + a_3 + \cdots = \sum_{k=1}^\infty a_k, \end{equation}$$
is known as an infinite series. Such series appear in many areas of modern mathematics. Much of this topic was developed during the seventeenth century. Leonhard Euler continued this study and in the process solved many important problems. In this article we will explain Euler's argument involving one of the most surprising series. \par You are likely to have already met perhaps the most important series which is the {\em geometric progression}. Given constants $a$ and $r$ we want to sum
$$\begin{equation} a + ar + ar^2 + \cdots + ar^N. \end{equation} $$
If $|r|<1$ we can make sense of the infinite sum – something known by Newton – which is
$$\begin{equation}\label{eq:gp} a + ar + ar^2 + \cdots + ar^N + \cdots = \frac{a}{1-r}. \end{equation}$$
This was one of the first, and only, general results known during the seventeenth century. Another series then known was \begin{eqnarray} \sum_{k=1}^\infty \frac{2}{k(k+1)} & = & 1 + \frac{1}{3} + \frac{1}{6} + \frac{1}{10 }+ \frac{1}{15} + \cdots \\ & = & 2 \left[ \frac{1}{2} + \frac{1}{6} + \frac{1}{12}+ \frac{1}{20} + \cdots \right] \\ & = & 2 \left[ \left( 1 - \frac{1}{2}\right) + \left( \frac{1}{2} - \frac{1}{3}\right) + \left( \frac{1}{3} - \frac{1}{4}\right) + \left( \frac{1}{4} - \frac{1}{5}\right) + \cdots \right] \\ & = & 2 \label{eq:Bernoulli}. \end{eqnarray} Similar methods were used to find the sums \begin{equation} \sum_{k=1}^\infty \frac{k^2}{2^k} = 6 \quad\mbox{and}\quad \sum_{k=1}^\infty \frac{k^3}{2^k} = 26. \end{equation} Now all these series converge. That is to say we can make sense of the infinite sum as a finite number. This is not true of a particularly famous series which is known as the {\em harmonic series}: \begin{equation} 1 +\frac{1}{2} +\frac{1}{3} +\frac{1}{4} + \cdots = \sum_{k=1}^\infty \frac{1}{k}. \end{equation} \par The following medieval proof that the harmonic series diverges was discovered and published by a French monk called Orseme around 1350 and relies on grouping the terms in the series as follows:
\begin{eqnarray} & & 1 +\frac{1}{2} +\frac{1}{3} +\frac{1}{4} +\frac{1}{5} +\frac{1}{6} +\frac{1}{7} + \cdots\\ & = & 1 +\frac{1}{2} + \left(\frac{1}{3} +\frac{1}{4}\right) + \left(\frac{1}{5} +\frac{1}{6} +\frac{1}{7} +\frac{1}{8}\right) +\left( \frac{1}{9} +\frac{1}{10} +\frac{1}{11} +\frac{1}{12} +\frac{1}{13} +\frac{1}{14} +\frac{1}{15} +\frac{1}{16}\right) + \cdots\\ & \geq & 1 +\frac{1}{2} +\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+ \cdots \end{eqnarray}

The harmonic series diverges
It follows that the sum can be made as large as we please by taking enough terms. In fact this series diverges quite slowly. A more accurate estimate of the speed of divergence can be made using the following more modern proof. This uses a technique known as the {\em integral test} which compares the graph of a function with the terms of the series. By integrating the function using calculus we can compare the sum of the series with the integral of the function and draw conclusions from this. \par In this case we compare terms in the series with the area under the graph of the function $1/(1+x)$. In particular, figure 1 shows that \begin{equation} \sum_{k=1}^n\frac{1}{k} >\int_0^n \frac{1}{1+x}\mathrm{d}x. \end{equation}
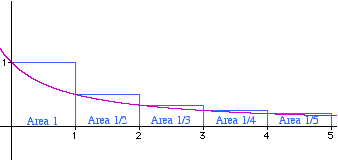
Figure 1: The series 1/n above the graph of 1/(1+x)
Of course the integral on the right is easy. Solving this gives \begin{equation} \sum_{k=1}^n\frac{1}{k} > \ln(1+n). \end{equation} Now, the function $\ln(1+n)$ is unbounded. By this we mean that there is no limit to how big we can make it by taking sufficiently large values of $n$. So we can make $\sum_{k=1}^n\frac{1}{k}$ as large as we please. A similar argument comparing the series to the function $1/x$ shows that \begin{equation} 1+ \ln(n)> \sum_{k=1}^n\frac{1}{k} > \ln(1+n) \end{equation} so that we can estimate how fast the series diverges.
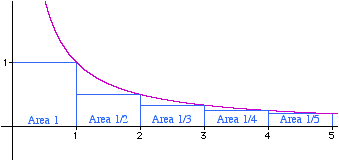
Figure 2: The series 1/n below the graph of 1/x
The harmonic series generalised
The harmonic series can be described as "the sum of the reciprocals of the natural numbers". Another series that presents itself as being similar is the "the sum of the squares of reciprocals of the natural numbers". That is to say, the series \begin{equation}\label{eq:basel} 1 +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} + \cdots = \sum_{k=1}^\infty \frac{1}{k^2}. \end{equation} The first question we ask is "Does this series converge?". If it does we next ask "What is the sum?". To answer the first question we notice that \begin{equation} 2k^2 \geq k(k+1), \end{equation} and so \begin{equation} \frac{1}{k^2} \leq \frac {2}{k(k+1)}, \end{equation} and comparing with terms in the series (4) that we encountered earlier gives that \begin{equation} \sum_{k=1}^\infty \frac{1}{k^2} \leq \sum_{k=1}^\infty \frac{2}{k(k+1)} = 2. \end{equation}

Bust of Leibniz by Johann Gottfried Schmidt
The series converges, but the exact value of the sum proves hard to find. Jakob Bernoulli considered it and failed to find it. So did Mengoli and Leibniz. Finding the sum became known as the Basel Problem and we concentrate on Euler's solution for the rest of this article.
"Infinite polynomial" - power series
Before solving this problem we look briefly at a piece of theory Euler used which allowed him to write the function $\sin(x)$ in a particular way. This really could (or perhaps should) be the subject of an article in its own right. What Euler knew, as as we will see in a moment, is that $\sin(x)$ can be written as an " infinite polynomial" in the following way: \begin{equation}\label{eq:taylorsin} \sin(x) = x - \frac{x^3}{3!} +\frac{x^5}{5!} -\frac{x^7}{7!} + \cdots + (-1)^{k}\frac{x^{2k+1}}{(2k+1)!} + \cdots \end{equation} This is called a {\em power series} for $\sin(x)$ because it is a series in terms of powers of $x$. You may be aware that you can approximate $\sin(x) \approx x$ when $x$ is small. This just uses the first term in the series above. You can get better approximations to $\sin(x)$ as \begin{equation} \sin(x) \approx x - \frac{x^3}{3!} \end{equation} and \begin{equation} \sin(x) \approx x - \frac{x^3}{3!} +\frac{x^5}{5!} \end{equation} by taking successive terms. Most other functions, such as $\cos(x), e^x, \ln(x),$ etc. have power series. It is series such as these that your pocket calculator uses to calculate numerical values. In formula (20) $x$ is in {\em radians} not degrees and it would not be nearly so beautiful if $x$ was an angle in degrees. In fact, one of the reasons we choose to use radians is {\em because} this allows us to write the formula in this way.
Euler's solution to the Basel Problem

Leonhard Euler
Euler was working on the Basel Problem at the age of 24 in 1731 by calculating a numerical approximation. This is an arduous task by hand with a series which converges as slowly as this. In 1735 he arrived at the following exact result: \begin{equation} \sum_{k=1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6}. \end{equation} This is a truly remarkable result. No one expected the value $\pi$, the ratio of the circumference of a circle to the diameter, to appear in the formula for the sum. Euler starts with an $n$th degree polynomial $p(x)$ with the following properties:
- $p(x)$ has non-zero roots $a_1,\cdots,a_n$,
- $p(0)=1$.
Then $p(x)$ may be written as a product in the following form: \begin{equation} p(x) = \left(1-\frac{x}{a_1}\right) \left(1-\frac{x}{a_2}\right) \cdots \left(1-\frac{x}{a_n}\right). \end{equation} We paraphrase Euler's next claim as {\em "what holds for a finite polynomial holds for an infinite polynomial"}. He applies this claim to the polynomial \begin{equation} p(x) =1 - \frac{x^2}{3!} +\frac{x^4}{5!} -\frac{x^6}{7!} + \cdots \end{equation} which is an infinite polynomial with $p(0)=1$. Furthermore, as Euler knew, $\sin(x)$ can be written as a series: \begin{equation} \sin(x) = x - \frac{x^3}{3!} +\frac{x^5}{5!} -\frac{x^7}{7!} + \cdots + (-1)^{k}\frac{x^{2k+1}}{(2k+1)!} + \cdots \end{equation} Multiplying $p(x)$ by $x$ he obtained \begin{equation} x p(x) = x - \frac{x^3}{3!} +\frac{x^5}{5!} -\frac{x^7}{7!} + \cdots = \sin(x). \end{equation} This has zeros at $x=\pm k\pi$ for $k=1,2,\cdots$ since these are the zeros of $\sin(x)$. We can now use the claim above and write $p(x)$ as an infinite product and equate the two as \begin{eqnarray} & & 1 - \frac{x^2}{3!} +\frac{x^4}{5!} -\frac{x^6}{7!} + \cdots = p(x) \\ & = & \left(1-\frac{x}{\pi}\right) \left(1+\frac{x}{\pi}\right) \left(1-\frac{x}{2\pi}\right) \left(1+\frac{x}{2\pi}\right) \times \cdots\\ & = & \left[1-\frac{x^2}{\pi^2}\right] \left[1-\frac{x^2}{4\pi^2}\right] \left[1-\frac{x^2}{9\pi^2}\right] \times \cdots \end{eqnarray} The second line pairs the positive and negative roots -- the last line uses the difference of two squares to combine these. If you don't believe this can be done you are right to question the logic here! Euler is being incredibly bold in his assertion that "what holds for a finite polynomial holds for an infinite polynomial". His use turns out to give the correct answer in this case! \par Euler's trick is to write $p(x)$ in two different ways. He exploits this by expanding the right hand side. This infinite product will be very complicated but there will be a constant term $1$ and one can collect the $x^2$ term without too much effort as follows: \begin{equation} 1 - \frac{x^2}{3!} +\frac{x^4}{5!} -\frac{x^6}{7!} + \cdots = 1 - \left( \frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \frac{1}{16\pi^2} + \cdots \right)x^2 + \cdots \end{equation} Now Euler equates the coefficients of $x^2$ to conclude that \begin{equation} -\frac{1}{3!} =- \left( \frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \frac{1}{16\pi^2} + \cdots \right), \end{equation} which gives \begin{equation} 1 +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} + \cdots = \frac{\pi^2}{6}. \end{equation} Now Euler didn't stop here -- he expanded the product further and equated other coefficients to sum other series. In this way he obtained \begin{equation} \sum_{k=1}^\infty \frac{1}{k^4} = \frac{\pi^4}{90} \quad \mbox{and} \quad \sum_{k=1}^\infty \frac{1}{k^6} = \frac{\pi^6}{945}. \end{equation} In 1744 he obtained \begin{equation} \sum_{k=1}^\infty \frac{1}{k^{26}} = \frac{2^{24} 76977927 \pi^{26}}{27!} \end{equation} by this method. In principle his method solves \begin{equation} \sum_{k=1}^\infty \frac{1}{k^{2n}} \end{equation} for all natural numbers $n$.
Extensions of the Basel problem
In a style typical of Euler, he not only solved the problem in hand but also used the method to solve a class of related problems. You will notice that his method only works for {\em even} powers. What then, about \begin{equation} \sum_{k=1}^\infty \frac{1}{k^3}? \end{equation} The answer is: {\em we don't know}. This is still an open problem, and quite a famous one. Euler tried to solve it of course, but failed. The best he could do was \begin{equation} \sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)^3} = 1 - \frac{1}{27} + \frac{1}{125} - \cdots = \frac{\pi^3}{32}. \end{equation}
Further reading
You can find out more about some on Euler's work on infinite series (including a derivation of the last result) in his paper Remarques sur un beau rapport entre les series des puissances tant directes que reciproques.
About the author

Chris Sangwin is a member of staff in the School of Mathematics and Statistics at the University of Birmingham. He is a Research Fellow in the Learning and Teaching Support Network centre for Mathematics, Statistics, and Operational Research. His interests lie in mathematical Control Theory.
Comments
Anonymous
Thanks very much for the detailed explanation. It was very helpful.
Anonymous
Hope that I can live until they discover the solution for any zeta function.
Anonymous
Nah, maths develop slowly, you not going be alive when new maths came out.
John Barker
Hi Chris!!!
Anonymous
interesting!
Anonymous
Nice article - i had not seen Euler's method before, thank you.
Anonymous
Very well written and interesting. Regards
Anonymous
Great article. Just a minor hint:
The sum for 1/( k^3 ) is known since 1979:
It's called the Apér'y Constant.
Source:
http://en.wikipedia.org/wiki/Ap%C3%A9ry%27s_constant
Cheers,
Gerhard Tscheinig
Rachel
Anonymous
Sorry, but Apery only proved that it is irrational and that too by following the methods of Leonhard Euler and still the value of this infinite series in unknown. The value has as such been called Apery constant but it is still an open problem for great minds to solve
Anonymous
Hi!
First of all I just wanted to say this is all very well written so thanks.
I am in particular searching for a closed solution for partial sum of the basel problem but can't find it :-(
Anonymous
Thank you Chris Sangwin
This material is useful.
Anonymous
Nice article.
Tiny point.
Figure 2 caption should be ...below the graph of 1/x.
Marianne
Thanks for spotting that! We've corrected it.
Anonymous
Euler solves the Basel problem by applying the Newtonian formulae for converting an infinite summation series into an infinite product series, and vice versa. The Newtonian formulae are explained on pages 358-359 of D.T.Whiteside's Mathematical Papers of Isaac Newton vol 5. This comment submitted by Peter L. Griffiths.
Anonymous
It was really interesting! I think there is also a solution with fourier series.
Anonymous
It is important to mention Euler's discovery in 1755 that the cotangent series generates the zeta evaluations. comment submitted by Peter L. Griffiths.
Anonymous
On line (?) 26, i think it should be
(-1)^k
instead of
(-1)^k+1
Not sure if i'm right or just missing something...
anyway very interesting and useful article thank you
Marianne
Thanks for pointing that out! We've fixed the error.
Anonymous
Are equation (24) and equation (25) equal ?
I don't understand the Euler's claim in equation (25).
Marianne
Hi! No, the two formulae are not equal as (24) is finite and (25) is infinite. The way Euler's claim is applied is explained in the text between equations (27) and (28): xp(x) is a polynomial with certain roots, whch as in the finite case, can be written as a product.
Anonymous
Hi, stupid question probably but where does eqn 24 come from!? It doesn't look right. Suppose for example you take p(x) = x^2 - 4, then (24) says p(x) = (1-x/2)(1+x/2), but it doesn't (multiplying out you get 1 - x^2/4, which is not p(x)).
Marianne
Point (2) says that p(0)=1, which isn't the case for p(x)=x^2-4.
Anonymous
for any equation p(x)=0 (where p(x) is an expression or function of x) has roots a0, a1,....then at x=a0, a1,... p(x) becomes 0. in your example, p(x)=1 - x^2/4. At x=2 or -2, i.e., p(2)=p(-2) = 0.
Anonymous
Er,it seems your polynomial p(x)=x*2-4 doesn't agree with the condition p(0)=1
Anonymous
for the excellent and beautifull explanation
Anonymous
Where can one find more detail about Eulers assumptions he made in this proof and how his assumptions were taken care of later?
Peter L. Griffiths
The proof of the sine Basel conjecture (PI)^2/2 = 1 + 1/2^2 + 1/3^2 + 1/4^2 .... depends on the Newtonian Infinite Series formulae which are
the ABC summation 1 + Ax + Bx^2 + Cx^3 .... = (1+ax)(1+ bx)(1 +cx)....
the ABC Alternating 1 -Ax + Bx^2 - Cx^3 .... = (1- ax)(1- bx) (1- cx) ...
the A summation Ax = ax + bx + cx..... which seems to be a special case of the sine Basel conjecture (PI)^2 = 1 + 1/2^2 + 1/3^2 + 1/4^2 .....
with both sides multiplied by (u/PI)^2 and thus becomes u^2/6 = (u/PI)^2 + (u/2PI)^2 + (u/3PI)^2 .... clearly a version of the A summation
Au^2 = au^2 + bu^2 + cu^2 ... with A = 1/6, a =(1/PI)^2, b = (1/2PI)^2, c = (1/3PI)^2.
The alternating sine series is (sinu)/u = 1 - u^2/3! + u^4/5! - u^6/7!.....clearly a special case of the ABC Alternating, whose product series can now be
evaluated by substituting values for letters.
saurabh
x=(1/e)^(1/e)^(1/e)...............
What is the value of x
Halil
lim[x=infinite]((1/e)^(1/e)^x))
powers of power are multiplied.
buddy
find by applying ln
Peter W. Kacensky
Hi Chris:
Two years ago I discovered some interesting equations involving odd positive integer zeta values, and recently I derived some equations using Euler's L-number equations (which sum to odd powers of Pi). I believe I am the first person ever to derive these equations. I've been trying to find a closed form for zeta 3 for the last two years since I retired. I've written a few of these equations and derivations using Latex.
Would you be interested in seeing some of my work?
Pete Kacensky
peterkacensky@charter.net
phil p
can you please show us how to obtain zeta(4) from your presentation of zeta(2)?
Anonymous
Fascinating story told fascinatedly
Neal Batra
I am an IBDP student, currently revising for mocks. I use the haese mathematics textbook and am always shocked by how much effort would have gone into producing this textbook. Out of curiosity, I decided to search the name of the authors up and I came across you Mr. Sangwin! I am just writing this as a thank you for the time that must have taken to produce a textbook of such high quality and hopefully if I meet my offer, see you in September 2024!