Mathematical mysteries: Chomp
Chomp is a simple two-dimensional game, played as follows.
Cookies are set out on a rectangular grid. The bottom left cookie is poisoned.

Two players take it in turn to "chomp" - that is, to eat one of the remaining cookies, plus all the cookies above and to the right of that cookie.
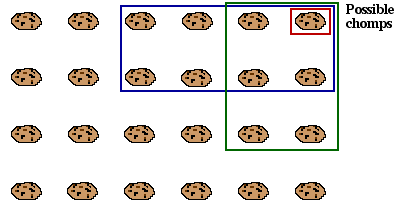
The loser is the player who has to eat the poisoned cookie.
We can ask if either player has a winning strategy, that is, can one player, before starting play, be sure of winning?
The answer to this question is yes. One of the players is sure to have a winning strategy. This is easy to see, because the game must finish in finitely many moves, and can't be drawn. In fact, the person who plays first can be certain of winning, if they make the right moves. To see this, suppose the first player (Player A) makes the first move by chomping just the top right-hand cookie. Then either this is the first move of a winning strategy for Player A, or there is a reply which is the first move of a winning strategy for Player B. If the latter is the case, then Player A could have opened with that very move and been guaranteed a win.
So what is the winning strategy for Player A? Well, that is the mystery - nobody knows! The proof that there is a winning strategy for the first player was very simple - but didn't describe the strategy. No one has ever been able to do that. Maybe you can!
There are some simple cases where a winning strategy can be described - Square Chomp and Thin Chomp. Square Chomp is Chomp played on a square grid, and Thin Chomp is Chomp played on a grid that is only two squares wide. See if you can find the winning strategies in these special cases - or find out how if you get stuck.
About the author
Helen Joyce is an assistant editor of Plus.
Thanks to John Webb of the University of Cape Town in South Africa for telling me about Chomp.
Comments
Anonymous
"One of the players is sure to have a winning strategy. This is easy to see, because the game must finish in finitely many moves, and can't be drawn."
Is that "easy to see"?
It implies a theorum: "If a game must finish in finitely many moves, and can't be drawn, then there must be a winning strategy for one player."
No doubt it's "easy to see" once explained, but it's far from obvious to ne... it would be nice to have an explanation, or proof....
Anonymous
Label a position a winning position if there is at least one move to a losing position, a losing position as one with no moves to non-winning positions, and a drawing position as one where there is no move to a losing solution, but there is a move to a drawing position. The final position(s) are unknown, but they are not . The first player has a winning strategy on a position when it is a winning position, and the second player has a winning strategy if it is a losing position (this should at least be obvious). Therefore, the only time when neither player has a winning strategy is in a drawing position.
Consider such a drawing position. By definition there is a move to another drawing position. However, that creates an infinite sequence of moves, which contradicts the original assumption that the game is finite. Therefore there are no drawing positions, and every finite game that cannot end in a draw has a winning strategy for one of the players.
Note: This argument doesn't work for infinite games. There are some (highly interesting) infinite games that cannot end in a draw, but neither player has a winning strategy.
Alkis
Nice presentation. Indeed it seems that there is no strategy ... I have tried a lot to find one, but I gave up. I have tried with chomps of max size 3x3 (squares or rectangles) and I could always win. Yet, I still could not formulate a strategy. However, I suppose there is one, because playing Philip Brocoum's Munch 5x6, an excellent version of Chomp game, the computer *always wins* if the human plays (always first) with no winning strategy. (How can one have a strategy there cannot be any?) However, the computer/Brocoum seems to have some kind strategy! Unfortunately, I could not find Brocoum's email anywhere. Maybe you can contact him? He might have some interesting data to share ...
Andy Deighton
There has to be a winning strategy for the first person to move. It might not be possible to write the strategy down as a simple to follow rule-of-thumb. In terms of game theory it will always be possible to compute a tree of all outcomes from all moves to select a winning strategy, for a massive initial grid, this calculation might eventually become practically impossible. The article says that no one has yet found a 'strategy' - but playing a move that leads to wain is always a strategy.
Higming
This is the way to win it
First take the candy at (3,2) and then it depends on the opponent's next move.
If he picks one from the top, take (1,5) and then he's probably gonna take (6,1).
Take (3,2). Then you win no matter what. If he takes (5,1) take (1,4) if he takes (2,2), take (4,1) I think you'll know how to go from there.
If he takes (5,1) take (1,4), then he is going to take (4,1) so take 2,2 after that. Then you can continue.
If he takes 6,1 then take 2,2 and then copy what he does and you'll win.
If he takes 4,1 then take 1,3 and if he takes 3,1 take 2,2 and vice versa.
So there you have it!
vab10266
Two questions.
Which corner is (0,0)?
What size is the grid you are playing on?
Andy Deighton
first to move loses on the 1x1 grid - on any other sized grid, the first to move has won - for example with n x 1 the first to move can take n - 1 squares and win. With a grid a million by a trillion, the first to move also has a winning strategy, but I've no idea what it is.
David
I made a 2 player game of Chomp for the iPhone and iPad. Im still currently working on the single palyer mode but im still stuck on my algorithm. If you want to check out what I got the link is https://itunes.apple.com/us/app/choco-chomp/id1213722025?mt=8. It also includes an iMessage extention which is what im most proud of.