
Maths in a minute: Chomp
Chomp is a simple game with a surprising mathematical twist. The rules are as follows.
Cookies are set out on a rectangular grid. The bottom left cookie is poisoned.

The bottom left cookie is poisoned.
Two players take it in turn to "chomp" — that is, to eat one of the remaining cookies, plus all the cookies above and to the right of that cookie.
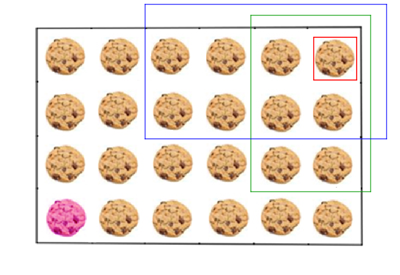
Possible moves in Chomp.
The loser is the player who has to eat the poisoned cookie.
We can ask if either player has a winning strategy, that is, can one player, before starting play, be sure of winning?
The answer to this question is yes. One of the players is sure to have a winning strategy. This is easy to see, because the game must finish in finitely many moves, and can't be drawn. In fact, the person who plays first can be certain of winning, if they make the right moves. To see this, suppose the first player (Player A) makes the first move by chomping just the top right-hand cookie. Then either this is the first move of a winning strategy for Player A, or there is a reply which is the first move of a winning strategy for Player B. If the latter is the case, then Player A could have opened with that very move and been guaranteed a win.
So what is the winning strategy for Player A? Well, that is the mystery — nobody knows, at least not in general! The proof that there is a winning strategy for the first player was very simple — but didn't describe the strategy. It's a so-called non-constructive proof and nobody has ever been able to come up with a constructive version.
For a sufficiently small grid a computer could of course work through all possible combinations of moves to find a winning strategy, but that's not a particularly interesting approach. More interesting are two simple cases where a winning strategy can be described: Square Chomp and Thin Chomp. Square Chomp is Chomp played on a square grid, and Thin Chomp is Chomp played on a grid that is only two squares wide. See if you can find the winning strategies in these special cases — or find out how if you get stuck.
Comments
Paulo
Player 1 (P1) eats the cookie just one row above and one column to the right of the poissoned one, leaving two "legs". P2 picks to eat one cookie of one of the two legs, leaving say m cookies above (or to the right) of the poissoned one. P1 eats the corresponding cookie of the other leg, leaving the same m cookies on this leg: in this way symmetry is preserved. This evolves untill P2 leaves no cookies on a leg. P1 wins!
Paulo
Sorry... the proposed solution doesn't work for the "Slim Chomp"!