
Mission to Mars
The race for Mars is on. The European Space Agency's Mars Express mission and the first of two US Mars Exploration Rovers launched by NASA are currently hurtling toward the red planet, each hunting for water and possible signs of life. But why this flurry of activity? Is it simply the spirit of competition that has driven the parallel missions?
In fact, the reason both space agencies have simultaneously decided to launch now is to take advantage of the close encounter between Mars and Earth that occurs every 17 years due to the dance of the two planets' orbits. All the planets move around the sun in elliptical orbits, as Kepler first realised early in the 17th century. Out of years of hard work analysing astronomical data, he developed three Laws of Planetary Motion:
- A planet moves around the Sun in an elliptical orbit which has the Sun at one of its two foci;
- The line joining a planet to the Sun sweeps out equal areas in equal times as the planet moves on its orbit;
- The square of the period of a planet is proportional to the cube of its mean distance from the Sun;
Earth's orbit lies inside the more elliptical orbit of Mars. From Kepler's third law, we know that the time it takes Earth to orbit the Sun (365 days) is less than the time it takes Mars (687 days). So the Earth overtakes Mars every 26 months - at this point, called an opposition, the Earth is between the Sun and Mars.
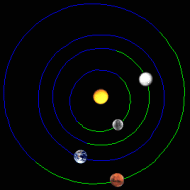 2 June 2003: Earth (the second planet in) is catching up to Mars (the outer planet) |
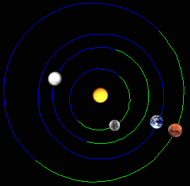 27 Aug 2003: Perilic opposition |
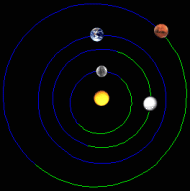 26 December 2003: Mars Express arrives, and the Earth is now in front of Mars |
It is a good idea to launch a space mission to Mars around an opposition, leaving before and arriving after, as this will make the journey shorter than any other time during the orbit. Explaining why, Dr Myles Standish, an astronomer from NASA's JPL, compared Earth and Mars to two cars on concentric race tracks.
"If you were in the car on the inside track and wanted to throw a ball to someone in the car on the outside, you can do it only at certain times: you have to throw the ball outward at a specific time before your car has caught up with the outside one, and you have to aim at a spot ahead of the outside car," Standish said. "It is very similar with spacecraft."
What makes the opposition in 2003 special is that it occurs when Mars is at the closest point in its orbit to the Sun, called the perihelion. These perihelic oppositions only occur every 15 to 17 years, and bring Mars significantly closer - around 55 million km - to the Earth, than at other times in their orbits (the distance can be as great as 99 million km).
In fact, the encounter in August 2003 will be the closest between Mars and Earth in not just the last 17 years, but the last 60,000 years! This is because the elliptical orbits of the planets are slowly moving in space, and as the long axis of the orbits of Earth and Mars begin to coincide, the perihelic opposition is occurring closer to the time Earth is at its furthest point from the Sun (the aphelion). Even closer encounters are predicted over the next millennia.
"Earth's aphelion and Mars' perihelion are still not in the same direction, but they're getting closer during this present era," Standish told www.space.com. "The alignment motion is so slow - thousands of years - that the bodies will pass through the right spots a number of times [during their regular orbits] while the alignment is quite close."
This particularly close pass doesn't make that much difference to Mars mission planners. The important thing is the timing of the launch and landing around an opposition, and in particular the 17 year perihelic pass. It will, however, make a difference to stargazers here on Earth. When Mars is at its closest in August, it will outshine all the stars in the night sky. And in December, when the missions arrive at the planet, we will turn our gaze to the TV for news of life on Mars.
Links:
NASA's Mars Exploration Rover mission
A history of our understanding of the orbits at the MacTutor History of Mathematics archive
A detailed look at gravity and Kepler's laws at PhysicsNet - follow the Gravity link