Researchers from the University of Maryland have devised a new kind of random number generator that is cryptographically secure, inherently private and — most importantly — certified random by the laws of physics.

Randomness is important, particularly in the age of the Internet, because it guarantees security. Valuable data and messages can be encrypted using long strings of random numbers to act as "keys", which encode and decode the information. Randomness implies unpredictability, so if the key is truly random, it's next to impossible for an outsider to guess it (see the Plus article Cracking codes for an example).

Physical contraptions like those used to draw lottery numbers can generate random number sequences, but they're unsuitable in the electronic age, and of course they might be rigged. Besides, there is a philosophical objection. Since the macroscopic laws of physics are deterministic, someone with full knowledge of the initial set-up of the machine and the conditions in the room could in theory calculate the outcome of the draw. It's mostly a theoretical objection: the processes involved are what mathematicians call chaotic: even the smallest change in the initial set-up can dramatically change the outcome, making the calculation very difficult in practice. But the objection nevertheless raises the question of how to generate true randomness.

Lottery machines are unsuitable for the electronic age.

For practical purposes, cryptographers typically employ mathematical algorithms called pseudo-random number generators (PRNGs) to approximate the ideal. But the very fact that the number sequences are generated by an algorithm — a recipe — means that they are not truly random. On a practical level, the sequences generated by PRNGs may look random, but there's no guarantee that they are private. You can never be entirely certain that there aren't underlying patterns that have escaped your attention, but can be guessed by an adversary. What's more, your PRNG may have been tampered with, so that it spits out sequences that pass all tests of randomness, but are known to your adversary.

Now, however, a team of experimentalists from the Joint Quantum Institute at the University of Maryland , in partnership with European quantum information scientists, has demonstrated a method of producing a certifiably random string of numbers with guaranteed privacy, based on fundamental principles of quantum mechanics. They report their results in the 15 April 2010 issue of Nature.

"Classical physics simply does not permit genuine randomness in the strict sense," says JQI Fellow Chris Monroe, who led the experimental team. "That is, the outcome of any classical physical process can ultimately be determined with enough information about initial conditions. Only quantum processes can be truly random — and even then, we must trust that the device is indeed quantum and has no remnant of classical physics in it."

In quantum mechanics, the science of matter and energy on the smallest scales, specific properties of objects (such as the position of an electron or the polarisation of a photon) can be inherently uncertain. Although the probability of any particular property can be calculated in advance, those properties take on particular values only when measured, and the values they do take on are intrinsically random. So in theory, one could obtain a series of random numbers by performing a series of quantum measurements that are entirely independent of one another.

"Such a sequence would, of course, be intrinsically random," says Dzmitry Matsukevich of JQI, a coauthor of the report in Nature. "However, most people would probably prefer to buy an existing quantum device rather than build a quantum random number generator themselves. Unfortunately in this case it is very difficult to ensure that the device produces a string of random numbers that is not known to anyone else. For example, instead of a real quantum random number generator, someone might sell you a black box device that has a memory filled with random numbers loaded in advance. This device would probably pass all existing tests of randomness. But someone would still have a copy of all the numbers."

There is, however, a procedure that guarantees the presence of truly random quantum measurements, generated only at — and completely unique to — a particular place and time, which might be termed private randomness. It was invented by physicist John Bell in 1964 to test a central hypothesis of quantum mechanics: namely, that two objects such as photons or matter particles can enter an exotic condition called entanglement, in which their states become so utterly interdependent that if a measurement is performed to determine a property of one (which will, of course, be a random value), the corresponding property of the other is instantly determined as well, even if the two objects are separated by distances so large that no information could possibly pass between them after the measurement is made on the first object.

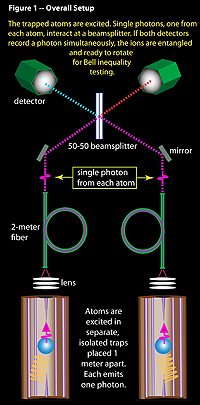
The new random number generator. See larger image.

Many scientists, notably including Albert Einstein, found that notion completely unacceptable, arguing instead that so-called "entangled" objects must actually possess some hidden variables which give the objects specific properties in advance of a measurement. Otherwise, a purely local measurement of Object 1 would have an instantaneous effect on Object 2, even if Object 2 was light-years away at the time of the measurement — a phenomenon Einstein dismissed as "spooky action at a distance." For 30 years, there was no convincing way of determining experimentally whether Einstein was right or wrong.

Then Bell came up with a revolutionary method that involved counting the correlations between measurements made on the two objects as the measuring devices were switched among numerous different orientations. Bell showed mathematically that if the objects were not entangled, their correlations would have to be smaller than a certain value, a condition that is expressed by an inequality. If they were entangled, however, the correlation rate could be higher, violating the inequality.

"Violation of a Bell inequality is possible only if the system obeys the laws of quantum mechanics," Matsukevich says. Therefore, if a system generates random numbers and at the same time allows you to verify a Bell inequality violation between isolated systems, you can be sure that real quantum processes are taking place, and that the randomness you generate is indeed private. As the authors say in their paper in Nature, "The violation of a Bell inequality guarantees that the observed outputs are not predetermined and that they arise from entangled quantum systems that possess intrinsic randomness."

The researchers performed more than 3,000 consecutive entanglement events in the course of about a month, confirming Bell inequality violation and in the process generating a string of private binary digits. As a result, they write in Nature, "we can, for the first time, certify that new randomness is produced in an experiment without a detailed model of the device." That is, the process relies only on achieving entanglement and performing operations on the entangled objects, not on the specific details of how entanglement was achieved. While various kinds of tests performed in recent decades on entangled systems have shown Bell inequality violation, the JQI experiment was the first to do so with sufficient accuracy to give meaningful results for random number generation.

In their experiment the JQI group placed a single atom in each of two completely isolated enclosures spaced a metre apart. They then proceeded to entangle the two atoms using a now-familiar method based on single photons travelling between the atoms. Every time their apparatus signalled that entanglement had been achieved, the researchers rotated each atom on its axis according to a random schedule, and then took a measurement of each atom's emitted light. The value from each of the two atoms was then used to generate a binary number. Using their observations to verify that Bell's inequality had indeed been violated, the researchers were able to show that their output string could be transformed into 42 truly random and private numbers. And while some randomness is required as input (deciding on the rotation of each atom), this randomness comes relatively cheap: the method can produce far longer number sequences than the random seed that needs to be supplied.

At present, "the random bit generation rate is extremely slow," said Monroe, "but we expect speedups by orders of magnitude in coming years as we more efficiently entangle the atoms, perhaps by using atom-like quantum systems embedded in a solid-state chip." Then by violating the Bell inequality over much larger distances, Monroe added that "such a system could be deployed for a more secure type of data encryption."