
Plus Advent Calendar Door #1: Fluid dynamics and the Euler equations
The motion of water, air, or indeed any fluid, is weird when you think about it. It moves as a continuous mass, and can move with great force, yet it is made up of tiny individually moving molecules. We know from personal experience that external forces, like gravity, or the push of an oar, can make water move, as can changing the pressure when we open a tap. And movement passes through a body of water, such as ripples moving across a pond.
In 1757 the mathematician Leonard Euler published a paper, General principles of the motions of fluids. The paper is remarkably readable (you can see both the original paper in French and an English translation). The concepts and notation are recognisable to us today as this paper marked the beginning of modern fluid dynamics, the study of how fluids (liquids and gases) move. The set of equations in the paper, now known as the Euler equations, crystalised the mathematical relationship between the movement of a fluid, the internal pressure, and any external forces (such as gravity) applied to it.
The Euler equations apply to any fluid that's not sticky, or viscous, to give it the technical term. You need the more complicated Navier-Stokes equations to describe the dynamics of a viscous fluid, and you can simplify these to get back to the Euler equations by ignoring viscosity. Viscosity isn't significant in the movement of ocean swell – big waves rolling across the open ocean – so let's see the Euler equations in action for this example.
Swell coming into a beach in Australia. Click to play movie.
The Euler equations
The Euler equations make use of the continuous nature of a fluid to describe the motion of the fluid at each instant and at each point, and how the motion relates to the internal pressure of the fluid at that point. For our example we can focus on the movement of the water in the direction of the wave, and look at the 2D vertical slice you get by cutting the wave vertically along the direction of travel.
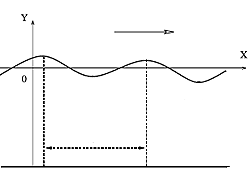
A vertical slice of the wave.
Points within the water on this slice can be described by coordinates $(x,y)$ where $x$ is the horizontal and $y$ the vertical direction. We can then write the motion of the water at a point $(x,y)$ and at time $t$ as $(u(x,y,t),v(x,y,t))$. This velocity of the water at the point can be describe by an arrow, also called a vector: it has a direction (the direction of the flow) and a magnitude (its speed). We write $P(x,y,t)$ for the pressure at point $(x,y)$ and time $t$. Pressure isn't a vector, it's just a number that varies across space and time.
The Euler equations for this example of the motion of the fluid in this 2D slice are: $$\frac{\partial{u}}{\partial{t}} + u \frac{\partial{u}}{\partial{x}} + v \frac{\partial{u}}{\partial{y}} = -\frac{\partial{P}}{\partial {x}}$$ $$\frac{\partial v}{\partial t} + u \frac{\partial{v}}{\partial x} + v \frac{\partial v}{\partial y} = -\frac{\partial P}{\partial y} - g.$$ The first equation describes how the change in velocity in the horizontal direction relates to the change in pressure and the interplay of the fluid motion in this direction. The second equation governs the vertical directions, so also includes $g$, the gravitational constant of acceleration, to account for the external force of gravity on the movement.
As the velocity and pressure of the fluid vary over both time and space, the Euler equations are partial differential equations to account for the rate of change with respect to these different quantities. For example the change in the velocity in the horizontal direction is written as $\frac{\partial{u}}{\partial{t}}$ stands for the partial derivative of $u(x,y,t)$ with respect to time.
Solving the Euler equations means finding the functions $u$, $v$ and $P$ whose partial derivatives satisfy the equations. The solution will also depend on certain boundary conditions, for example whether the surface of the water is flat or wavy.
Using the Euler equations it's possible to derive equations describing how water particles in our example of the ocean swell move. (Remember to think of these fluid particles at the macroscopic scale: they contain many many molecules of water but are so small that you can still think of them as a point within the fluid). The Euler equations show that ocean waves are not, as you might think, a moving wall of water. Instead the water particles move in small loops, which move along with the wave, though with a much slower speed.
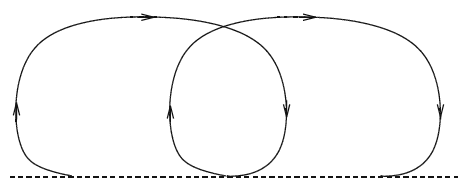
According to the Euler equations, the particles in ocean swell describe open loops, so the move along with the wave, though at slower speed. Image: Adrian Constantin.
Fluids are hard (to solve)
The Euler equations reveal one of the difficulties of understanding fluid dynamics – non-linearity. The fluid velocity interacts with itself – the motion of the water at one point is affected by the motion of the water nearby. This interaction could be linear, with the effects proportional to the causes, or it could be more complicated, what mathematicians call non-linear. In the Euler equations this nonlinear interaction is captured by terms like $$u\frac{\partial u}{\partial x} \;\;\;\; \mbox{and} \;\;\;\; v\frac{\partial u}{\partial y}, $$ in which the two components $u$ and $v$ of the velocity interact with themselves and each other.
The Euler equations were the first time nonlinearity had appeared in this sort of mathematical equation (it was the first nonlinear field theory). And this nonlinearity, combined with the difficulty in mathematically describing the boundary conditions, mean that the equations are almost impossible to solve in general. Solutions that are relevant to real waves, like our example above, have been found but they are only approximations. Most applications of the Euler equations that are relevant to the real world rely on computer simulations and computational fluid dynamics. And this is why approaches to solving the Euler equations, and the closely related Navier Stokes equations, continue to be an area of such intense mathematical research.
This article is based on Beneath the waves, you can read that article for more information for how Euler equations are used. You can also read more about the Navier Stokes equations and computational fluid dynamics on Plus.
Return to the Plus advent calendar 2021.
This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
