Beneath the waves

Swell coming into a beach in Australia. Click to play movie.

"There is something beautiful going on," says Adrian Constantin, a mathematician at King's College, London and the University of Vienna. He is talking about ocean waves, but the beauty he refers to is not so much about what you can see when you look at them. It's about the rich and delicate web of physical processes that go into making a wave what it is. Everything, from the speed of the wave to the pressure of the water, is connected. "It's amazing how rich this structure is," he says.

Ocean waves are not, as you might think, moving walls of water. "What moves along is some kind of energy," says Constantin. "The water does move along too, but not at the same speed as the wave. This is fortunate because if the oceans were moving along with the waves, the impact would be tremendous." Leonardo da Vinci captured the essence of waves beautifully back in the 15th century: "...the wave flees the place of its creation, while the water does not; like the waves made in a field of grain by the wind, where we see the waves running across the field while the grain remains in its place."

But then how does the water itself move? If you observed a little particle floating beneath the waves, would you see it staying put, or moving along? Is there a regular pattern to the motion at all, or are waves in general just too complex and chaotic to say something definite? These aren't just idle questions to ponder while watching the ocean — their answers may eventually help protect us from it too.

The Euler equation

Let's assume we are looking at the 2D slice you get by cutting the wave vertically along a line in the direction of travel.

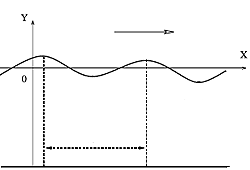
A vertical slice of the wave.

Points on this slice can be described by coordinates $(x,y)$ where $x$ is the horizontal and $y$ the vertical direction. Write $\vec{u} = (u(x,y,t),v(x,y,t))$ for the velocity at point $(x,y)$ and at time $t$ . Velocity is a vector: it has a direction (the direction of the flow) and a magnitude (its speed). Write $P(x,y,t)$ for the pressure at point $(x,y)$ and time $t$ . Pressure isn’t a vector, it’s just a number that varies across space and time. Euler’s equation is a differential equation, relating changes in velocity to changes in pressure. It can be written in two parts:

$\frac{\partial {u}}{\partial {t}} + u \frac{\partial {u}}{\partial {x}} + v \frac{\partial {u}}{\partial {y}} = -\frac{\partial {P}}{\partial {x}}$

$\frac{\partial v}{\partial t} + u \frac{\partial {v}}{\partial x} + v \frac{\partial v}{\partial y} = -\frac{\partial P}{\partial y} - g,$

where $g$ is the gravitational constant of acceleration and $\frac{\partial {u}}{\partial {t}}$ stands for the partial derivative of $u(x,y,t)$ with respect to time.

Solving this equation means finding the vector function $\vec{u}$ and the function $P$ whose partial derivatives satisfy the equation. The solution will depend on certain boundary conditions, for example whether the surface of the water is flat or wavy.

It's not easy to observe the swirling, whirling water underneath an ocean wave or to recreate one in the lab. One way of answering the question is to turn to maths. In the 18th century the mathematician Leonard Euler developed an equation which describes the dynamics of water. In fact, it applies to any fluid that's not sticky, or viscous to give it the technical term. "The waves I'm looking at are waves at sea, in oceanography they're called swell," says Constantin (the movie above shows such swell). "Viscosity effects are not dominant for waves that are relatively big and propagating in the open ocean and therefore can be neglected. So for this kind of purpose the governing equation is the Euler equation."

Dancing beneath the waves

Using the Euler equation it's possible to derive equations describing how water particles move. People have duly done this and come up with an idea of what happens beneath the waves. They found that water particles dance around in little closed loops in the shape of circles or ellipses. (See the image below.) People performed lab experiments too, photographing and filming particles floating in water, and they seemed to confirm the theory.

But there is a snag. The Euler equation, and the resulting equations of motion for water particles, are next to impossible to solve and the results about little closed loops are only approximate solutions. Part of the problem comes from the very fact that we're looking at waves. Since waves move, it's hard to establish how exactly the surface of the water behaves, but you need this knowledge to solve the equations. "Understanding how the upper boundary of the water moves in time, how it evolves, is one of the most difficult parts," explains Constantin.

Another problem comes from the fact that the velocity (the speed and direction of the water flow) interacts with itself: the velocity at one point is influenced by the velocity at points near-by. You can see this when you slowly pour some water into a fast-moving river. The slow-moving water particles you’ve poured in are quickly swept away by the current. This interaction could be linear, with the effects proportional to the causes, or it could be more complicated, what mathematicians call non-linear. In Euler’s equation this interaction is captured by terms like

$u\frac{\partial u}{\partial x} \; \; \; \; \mbox{and} \; \; \; \; v\frac{\partial u}{\partial y},$

in which the two components $u$ and $v$ of the velocity interact with themselves and each other. It is these terms that make the equation so hard to solve: they make it non-linear.

Photograph of the water particle orbits under a surface gravity wave. The particles seem to describe closed loops. Image: R.L. Wiegel & J.W. Johnson.

So you've got no choice but to simplify things to get approximate solutions. "One has to make things simple but not too simple because then all the fine connections that actually hold the key disappear," says Constantin. A standard way of simplifying the maths is to linearise the problem: loosely speaking, you simply ignore the offending non-linear terms whenever they become a nuisance, but you do so in a clever way. If you use such linearisation to infer the paths of particles the result appears to show that they do move in little ellipses or circles as the waves pass over them.

But the simplified theory also suggested something else. "If one does linear theory [to infer how the energy behaves] one sees that there should be some energy moving with the wave," explains Constantin. "So the water particles in the fluid experience, on average, a net displacement in the direction in which the waves are propagating." The two results are in conflict, indicating that the simplified theory is too crude. And indeed, there is photographic evidence suggesting that the little loops can become heavily distorted and even break up in steeper waves.

Constantin became intrigued by this problem out of simple curiosity. "I like to go diving in the summer and I like to watch the waves," he says. "I wondered, if the surface wave does this, then what happens underneath?" So Constantin took a fresh look at the problem, using more sophisticated techniques for analysing the governing equations. His results give a new, but equally pretty, picture: assuming that there are no underlying currents, particles whirl along in open loops, moving along with the waves but at slower speed. "The size of these loops depends on if the particle is deeper or higher up," he explains. "On the sea bed it's just a back and forth motion with some kind of forward drift, then the loops increase as you go vertically up and they are biggest at the top." The reason why lab experiments had shown up closed loops is that for waves that can be produced in the lab the forward drift is tiny, only a matter of millimetres. Only very recently have cameras become sensitive enough to pick up the fact that the loops are actually open and the particles moving along.

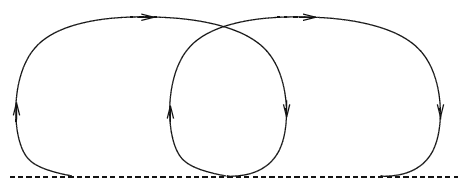
According to Constantin's results particles describe open loops, so the move along with the wave, though at slower speed. Image: Adrian Constantin.

Constantin's results don't apply to any type of wave, only to ones that follow an idealised pattern. That's the price you have to pay for being able to analyse the equations in depth, as it was for the previous theory too. For example, Constantin assumed that it's enough to look at a vertical slice of a wave, as the water behaves the same in any direction parallel to the crest line of the wave (see the box above). He also assumed that the waves have a symmetric profile that rises and falls exactly once per wavelength and that they travel at a constant speed over a flat sea bed. These (and other) assumptions aren't entirely realistic, but they are reasonable enough when it comes to describing ocean waves that have originated in a distant storm and are entering a region of calmer water in uniform flow.

Spotting monster waves

Constantin's work represents an important advance in our understanding of wave motion — so much so that he got invited to give one of the main lectures at this year's European Congress of Mathematics. But eventually it may also lead to important practical applications. One question that many people, from oil rig owners to those living on exposed coast lines, would like to have answered is how to predict when very big waves are approaching. One could simply observe the waves out at sea using cameras, but that requires a lot of man power. "The technical means are there but someone has to read off all the information," says Constantin.

Wave breaking is very difficult to describe mathematically. Image: misty.

But Constantin's work on particle paths not only helps to understand the velocity of the water underneath the waves. Euler's equation relates the velocity of the water to the pressure. "So by understanding what the velocity does one can try to understand what the pressure does." Now big waves alter the pressure on the sea bed, so one approach to forecasting the arrival of big waves would be to put pressure measuring devices at certain locations on the sea bed. "When you see large variations in pressure this tells you that there is something funny going on," he explains. "What exactly is going on is a natural extension of [my work]. But it's not finished yet, it's work in progress. The behaviour of the velocity field is related to the pressure in a complicated way, but still there is structure there. Some of it we understand and some we don't." Constantin is working on this problem with Walter Strauss, Joachim Escher and Gabriele Villari.

And there's another, much more dramatic thing about waves: they can break. Describing this breaking is infinitely more difficult than describing swell on the open ocean. "We have an idea what is going on through observations but it is impossible to put this in mathematical terms using the Euler equation, " says Constantin. "The mathematical tools and ideas don't exist. So one has to derive different simpler equations and this is only possible in certain regimes, for example for long waves with moderate amplitude. My colleague David Lannes and I have developed some models that capture the breaking and we are trying to refine and extend them. It's a matter of gaining some understanding from our models, going back [to observations], deriving more refined models and trying in this way to finally get to the core of the problem."

About the author

Adrian Constantin

Adrian Constantin was interviewed by Marianne Freiberger, Editor of Plus, at the European Congress of Mathematics in Krakow in July 2012.