Plus Advent Calendar Door #5: Asymptotes

Some curves get simple in the limit. As an example, look at the red curve below. As you move out to the right along the $x$-axis, the curve gets closer and closer to the horizontal blue line. And as you move up the $y$-axis, the curve gets closer and closer to the vertical blue line.

 

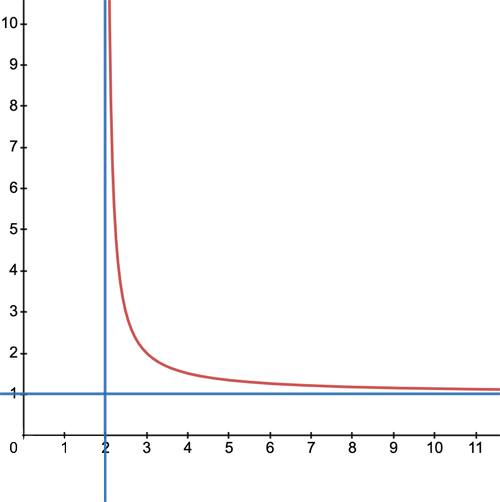
The blue lines are called the asymptotes of the curve: the distance between the curve and the respective asymptote tends to zero as either $x$ or $y$ tend to infinity. In this example the curve is given by the function \begin{equation}y=\frac{1}{x-2}+1.\end{equation} and the asymptotes are given by the equations $$y=1 \;\;\; \mbox{and} \;\;\; x=2.$$ Knowing a curve's asymptotes can be very useful. For example, imagine that the curve above tells you the value of some quantity (e.g. the money in you bank account) $x$ months from now, where $x$ is measured along the $x$-axis. Then even though it's a bit tricky to work out $y$ for a given $x$, knowing that the asymptote as $x$ goes to infinity is the horizontal blue line $y=1$ tells you that in the long run you'll have approximately £1 in your account.

Not all curves look like a straight line as $x$ or $y$ tend to infinity, so not all curves have asymptotes. But if they do (and of you are comfortable with limits) then you can find the asymptotes by taking the limit of the function describing the curve as $x$ or $y$ tend to infinity. In our example above this gives $$\lim_{x \rightarrow \infty} y = \lim_{x \rightarrow \infty}\frac{1}{x-2}+1=1.$$ That gives you the horizontal asymptote. Rearranging the expression (1) to phrase it in terms of $y$ gives $$x=\frac{1}{y-1}+2,$$ so $$\lim_{y \rightarrow \infty} x = \lim_{y \rightarrow \infty}\frac{1}{y-1}+2=2.$$ This gives you the vertical asymptote.

We leave you with an example of a pretty crazy curve and its perfectly uncrazy asymptote. The curve is given by a more complex parametric equation $$x=t+\frac{\cos{(14t)}}{t}, y=t+\frac{\sin{(14t)}}{t}, t>0.$$ The asymptote (to the wriggly part of the curve) as $x$ goes to infinity is the line $y=x$.

 

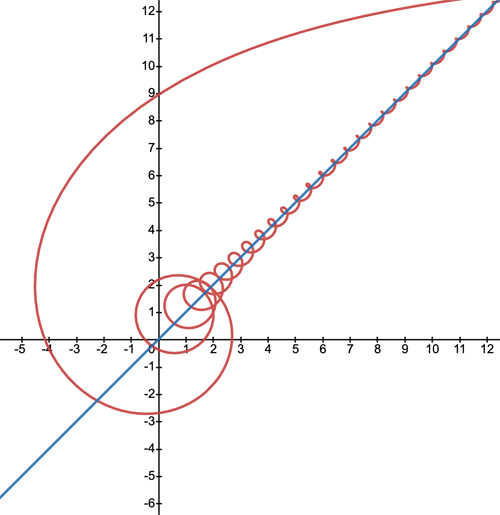
Thanks to Guillaume Jacquenot for posting this example on on Wikipedia.

This example again highlights how useful asymptotes are. It's not easy to work out the exact value of $y$ for a given $x$, but knowing the asymptote gives you a good approximation of $y$ for large $x$ — the larger $x$, the better the approximation.

Return to the Plus advent calendar 2021.

This article relates to the Applicable resurgent asymptotics research programme hosted by the Isaac Newton Institute for Mathematical Sciences (INI). You can see more articles relating to the programme here.

This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.