
Finding the volume of a tricky shape
January 1997
The PASS Maths logo depicts a sphere 'pierce d' by a cylinder embossed with the words PASS Maths. Our first puzzle concerns just such a shape, here referred to as The Ring.
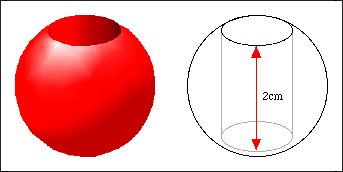
A ring is made from a solid sphere by drilling out a cylindrical hole through the sphere's centre. The axis of the cylinder goes through the centre of the sphere. When the ring is stood on a flat surface, it is exactly 2cm high. The question is, what is the volume of the solid material of the ring in cubic centimeters? You are also told that you have enough information to solve this problem.
We will publish the best solutions in the next issue, along with the answer to the problem itself.
Anonymous
Let R=sphere radius
Let r=cylinder radius
then sphere Cap height = R-1
considering that V.Sphere.Cap= 1/3*PI*(Cap.Hight)^2*(3*R-Cap.Hight)
=> V.Sphere.Cap = 1/3*PI*(R-1)^2*(3R-(R-1))
V.Sphere.Cap = 1/3*PI*(R^2-2R+1)(2R+1)
V.Sphere.Cap = 1/3*PI*(2R^3-3R^2+1)
V.Ring=Vol.Sphere -2*V.Sphere.Cape-V.cylender
V.Ring=4/3*PI*R^3 - 2*(1/3*PI*(2R^3-3R^2+1)) - 2*PI*r^2
but r^2=R^2 -1^2=R^2-1
substitute on above we get
V.Ring=4/3*PI*R^3 - 2*(1/3*PI*(2R^3-3R^2+1)) - 2*PI*R^2 + 2*PI
V.Ring=4/3*PI*R^3 - 4/3*PI*R^3 + 2*PI*R^2 -2/3*PI - 2*PI*R^2 + 2*PI
V.Ring= -2/3*PI + 2*PI
V.Ring= 4/3 *PI
Anonymous
I first saw his puzzle over 25 years ago when it concerned a mouse eating his way through a ball of cheese. I remember the date as I put the puzzle to my then future wife on St Valentine's day over a romantic(!) dinner date. Bemused, she allowed me to solve it on my napkin using integral of pi y squared dx.
But leaving that aside. Since you're not told of the diameter of the hole it can make no difference, so take the diameter as 0. You then have a sphere of radius 1cm whose volume will be 4/3 pi r cubed, (4.pi)/3.
As I said to her at the time: QED
Roy Lambert