
Puzzle page
Mathematical Misfits...continued
Last issue we ran two puzzles; one two-dimensional and one three-dimensional. Quite a few people solved the two-dimensional puzzle, but noone even got started on the three-dimensional one! So this issue we're giving the solution of the first part, and leaving the second part for next issue.The two-dimensional puzzle
Which fits best - a square peg in a round hole, or a round peg in a square hole?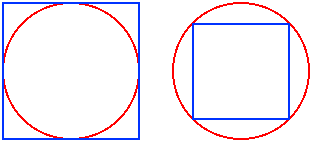
Which fits best?
The three-dimensional puzzle
Which fits best in a sphere - a dodecahedron or an icosahedron? That is, if you fit the largest possible dodecahedron and icosahedron inside a given sphere, which leaves least space?

Dodecahedron |

Icosahedron |
(Both images copyright by Rüdiger Appel)
Hints for the solution
If you can find the volume of one of these solids, the other shouldn't be hard, so we'll concentrate here on the dodecahedron.
The volume of a dodecahedron
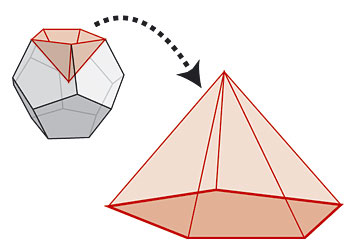
A Dodecahedron is 12 of these
We can think of the dodecahedron as a collection of twelve pyramids, each with one of the pentagonal faces as base, and the centre of the dodecahedron as the other vertex. Since the formula for the volume of a pyramid is one-third of the area of the base by the perpendicular height, we need to find both the area of a face and the distance from the centre of a face to the centre of the
dodecahedron.
First, the area of the face. This can be found using simple trigonometry, by noticing which lengths and angles are the same.
The key to finding the distance from the centre of a face to the centre of the dodecahedron is finding the dihedral angle - the angle each face makes with its neighbours. For this, it's useful to know about duality.
Dual polygons
Regular dodecahedra and icosahedra are dual to each other. This means that if you take one and put a vertex in place of every face, and a face in place of every vertex, you get the other!
Take the dodecahedron, for example. It has twelve pentagonal faces and a total of twenty vertices, each of which is a vertex of three of the faces. If you put a point at the centre of each face and join together those on adjoining faces, you get twenty equilateral triangle faces, and each vertex is a vertex of five faces - in other words, you get an icosahedron! The reverse works too - you can get a dodecahedron from an icosahedron.
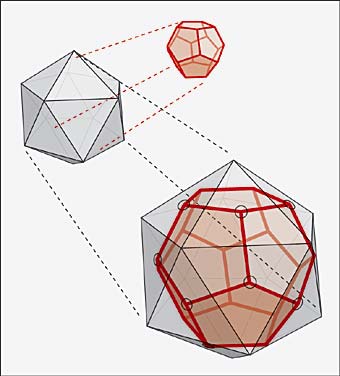
The dodecahedron and icosahedron are dual
If you are stumped by last issue's puzzle, here is the solution.