Solution to the taxi problem

We know that 85% of the taxis in Carborough are blue, the other 15% of taxis being green.

Suppose that there's no bias for any particular blue or green taxi to be involved in such incidents. Then consider 100 possible cases (contingencies), in which taxis are involved, in proportion to their numbers. Each case is equally probable. We expect 85 cases to involve blue taxis, 15 to involve green. If a blue taxi were really involved, the witness might report blue (with 80% probability) or green (with 20% probability). If a green taxi were really involved, the witness might report blue (with 20% probability) or green (with 80% probability). The number of times that these outcomes are expected to occur in each of these four cases are shown in the table below. (Tables like this are called contingency tables.)

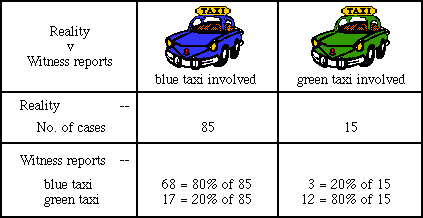
So, given that the witness reported seeing a blue taxi, we must use the row in the table corresponding to the reported blue taxi. We have 68+3 = 71 equally likely cases and the probability that a blue taxi really was involved is 68/71 = 96%.

A more interesting and surprising result is obtained in the case when the witness reports a green taxi. Many people on being asked this problem will say that if the witness reports a green taxi, then there is an 80% probability that a green taxi was involved. This however is incorrect, as the following argument shows. The contingency table is the same as above but now we must use the row in the table corresponding to the reported green taxi. We have 17+12 = 29 equally likely cases and the probability that a green taxi really was involved is 12/29 = 41%. The cases of correct identification of green are swamped by the false identifications of blue, and the witness's evidence is of no practical value.

Further reading:

New Scientist - "How right can you be?" by Robert Matthews, New Scientist 8 March 97. Matthews gives a full explanation and also describes other related problems.

Mathematics Today, December 1996 p168 - "Why is Weather forecasting Still Under a Cloud?" by Robert Matthews. Matthews examines mathematically why accurate short term forecasts are often thought by the public to be incorrect.