Unifying forces

A string universe. Image © R. Dijkgraaf.

To understand the ideas and aims of string theory, it's useful to look back and see how physics has developed from Newton's time to the present day. One crucial idea that has driven physics since Newton's time is that of unification: the attempt to explain seemingly different phenomena by a single overarching concept. Perhaps the first example of this came from Newton himself, who in his 1687 work Principia Mathematicae explained that the motion of the planets in the solar system, the motion of the Moon around the Earth, and the force that holds us to the Earth are all part of the same thing: the force of gravity. We take this for granted today, but pre-Newton the connection between a falling apple and the orbit of the Moon would have been far from obvious and quite amazing.

The next key unifying discovery was made around 180 years after Newton by the Scottish mathematician James Clerk Maxwell. Maxwell showed that electrostatics and magnetism, by no means similar phenomena at first sight, are just different aspects of a single thing called electromagnetism. In the process Maxwell discovered electromagnetic waves, which are in fact light — Maxwell had inadvertently explained a further seemingly different aspect of nature.

Another two hundred years on, in 1984, the Pakistani Abdus Salam and the American Steven Weinberg showed that the electromagnetic force and the weak nuclear force, which causes radioactive decay, are both just different aspects of a single force called the electroweak force.

This leaves us with three fundamental forces of nature: gravity, the electroweak force and the strong nuclear force which holds protons together.

Unifying matter

That deals with the forces, but what about matter? Many ancient belief systems have postulated that matter — and reality itself — is made from a finite number of elements. Modern physics confirms this idea. Experiments performed with the particle accelerator at CERN in Geneva have shown that there are just twelve basic building blocks of matter. These are known as the elementary particles. Everything we've ever seen in any experiment, here or in distant stars, is made of just these twelve elementary particles. (See Plus article The physics of elementary particles to find our more.)

All this is truly impressive: the entire Universe, its matter and dynamics explained by just three forces and twelve elementary objects. It's good, but we'd like to do better, and this is where string theory first enters: it is an attempt to unify further. To understand this, we have to tell another story.

Quantum gravity

There have been two great breakthroughs in the 20th century physics. Perhaps the most famous is Einstein's theory of general relativity. The other equally impressive theory is quantum mechanics.

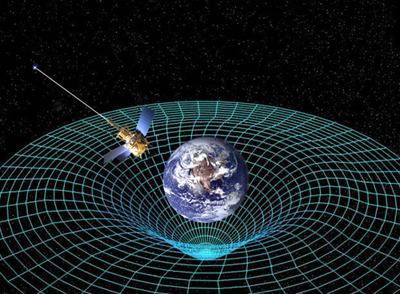
Massive bodies warp spacetime. Image coutesy NASA.

General relativity is itself a unification. Einstein realised that space and time are just different aspects of a single object he called spacetime. Massive bodies like planets can warp and distort spacetime, and gravity, which we experience as an attractive force, is in fact a consequence of this warping. Just as a pool ball placed on a trampoline will create a dip that a nearby marble will roll into, so does a massive body like a planet distort space, causing nearby objects to be attracted to it.

The predictions made by general relativity are remarkably accurate. In fact, most of us will have inadvertently taken part in an experiment that tests general relativity: if it were false, then global positioning systems would be wrong by about 50 metres per day. The fact that GPSs work to within five metres in ten years shows just how accurate general relativity is.

The other great breakthrough of the 20th century was quantum mechanics. One of the key ideas here is that the smaller the scale at which you look at the world, the more random things become. Heisenberg's uncertainty principle is perhaps the most famous example of this. The principle states that when you consider a moving particle, for example an electron orbiting the nucleus of an atom, you can never ever measure both its position and its momentum as accurately as you like. Looking at space at a minuscule scale may allow you to measure position with a lot of accuracy, but there won't be much you can say about momentum. This isn't because your measuring instruments are imprecise. There simply isn't a "true" value of momentum, but a whole range of values that the momentum can take, each with a certain probability. In short, there is randomness. This randomness appears when we look at particles at a small enough scale. The smaller one looks, the more random things become!

The idea that randomness is part of the very fabric of nature was revolutionary: it had previously been taken for granted that the laws of physics didn't depend on the size of things. But in quantum mechanics they do. The scale of things does matter, and the smaller the scale at which you look at nature, the more different from our everyday view of the world it becomes: randomness dominates the small scale world.

What happens to spacetime at small scales?

Again, this theory has performed very well in experiments. Technological gadgets that have emerged from quantum theory include the laser and the microchip that populate every computer, mobile phone and MP3 player.

But what happens if we combine quantum mechanics and relativity? According to relativity, spacetime is something that can stretch and bend. Quantum mechanics says that on small scales things get random. Putting these two ideas together implies that on very small scales spacetime itself becomes random, pulling and stretching, until it eventually pulls itself apart.

Evidently, since spacetime is here and this hasn't happened, there must be something wrong with combining relativity and quantum mechanics. But what? Both these theories are well-tested and believed to be true.

Perhaps we have made a hidden assumption?

It turns out that indeed we have. The assumption is that it's possible to consider smaller and smaller distances and get to the point where spacetime pulls itself apart. What has rested in the back of our minds is that the basic indivisible building blocks of nature are point-like — but this may not necessarily be true.

Strings to the rescue

This is where string theory comes to the rescue. It suggests that there is a smallest scale at which we can look at the world: we can go that small but no smaller. String theory asserts that the fundamental building blocks of nature are not like points, but like strings: they have extension, in other words they have length. And that length dictates the smallest scale at which we can see the world.

What possible advantage could this have? The answer is that strings can vibrate. In fact they can vibrate in an infinite number of different ways. This is a natural idea in music. We don't think that every single sound in a piece of music is produced by a different instrument; we know that a rich and varied set of sounds can be produced by even just a single violin. String theory is based on the same idea. The different particles and forces are just the fundamental strings vibrating in a multitude of different ways.

The mathematics behind string theory is long and complicated, but it has been worked out in detail. But has anyone ever seen such strings? The honest answer is "no". The current estimate of the size of these strings is about 10^-34m, far smaller than we can see today, even at CERN. Still, string theory is so far the only known way to combine gravity and quantum mechanics, and its mathematical elegance is for many scientists sufficient reason to keep pursuing it.

The theory's predictions

If string theory is indeed an accurate model of spacetime, then what else does it tell us about the world?

One of its more startling and most significant predictions is that spacetime is not four, but ten-dimensional. It is only in ten dimensions of spacetime that string theory works. So where are those six extra dimensions? The idea of hidden dimensions was in fact put forward many years before the advent of string theory by the German Theodor Kaluza and the Swede Oskar Klein.

Aerial view of the CERN site just outside Geneva. The underground particle accelerators (with circumferences of 27 km and 7 km) allow scientists to look at tiny scales. Image © CERN.

Shortly after Einstein described the bending of space in general relativity, Kaluza and Klein considered what would happen if a spatial dimension would bend round and rejoin itself to form a circle. The size of that circle could be very small, perhaps so small that it couldn't be seen. Those dimensions could then be hidden from view. Kaluza and Klein did show that in spite of this, these dimensions could still have an effect on the world we perceive. Electromagnetism becomes a consequence of the hidden circle with motion in the hidden dimension being electric charge. Hidden dimensions are possible and they in fact can give rise to forces in the dimensions that we can see.

String theory has embraced the Kaluza-Klein idea and currently various experiments are being devised to try and observe the hidden dimensions. One hope is that the extra dimensions may have left an imprint on the cosmic microwave background, the left-over radiation from the Big Bang, and that a detailed study of this radiation may reveal them. Other experiments are more direct. The force of gravity depends crucially on the number of dimensions, so by studying gravitational forces at short distances one can hope to detect deviations from Newton's law and again see the presence of extra dimensions.

Mathematics and physics have always influenced each other, with new mathematics being invented to describe nature, and old mathematics turning out to lend perfect descriptions for newly-discovered physical phenomena. String theory is no different and many mathematicians work on ideas inspired by it. These include the possible geometries of the hidden dimensions, the basic ideas of geometry when there is a minimum distance, the ways in which strings can split and come together, and the question of how we can relate strings to the particles in the world that we see.

String theory gives us an exciting vision of nature as miniscule bits of vibrating string in a space with hidden curled-up dimensions. All the implications of these ideas are yet to be understood. String theory is an active area of research with hundreds of people working to see how the theory fits together and produces the world we see around us.

For a more mathematical treatment of string theory read Plus article Tying it all up.

About this article

This article is part of the Researching the unknown project, a collaboration with researchers from Queen Mary University of London, bringing you the latest research on the forefront of physics. Click here to read more articles from the project.

David Berman is a lecturer in theoretical physics at Queen Mary University of London. He previously spent time at the universities of Manchester, Brussels, Durham, Utrecht, Groningen, Jerusalem and Cambridge as well as a year at CERN in Geneva.

His interests outside of physics include football, music and theatre and the arts.

This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.