On a clear day: solution
On a clear day: solution
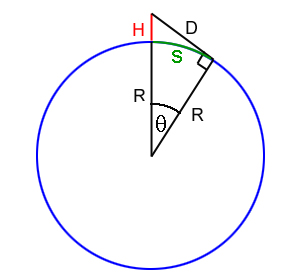
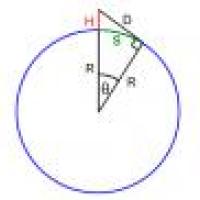
R is the radius of the Earth, H is your height and D is how far you can see. The walking distance across the Earth's surface is the length of the arc s.
Solution to problem 1: In Issue 54's Outer Space you were asked to work out the "walking" distance over the Earth's surface to the horizon. This is equal to the length $s$ of the arc of the circle from the point where you are to the point where your line of sight hits the surface of the Earth, which is $$s=R\theta$$ where $\theta$ is the angle as shown in the diagram and $R$ is the radius of the Earth. Now bearing in mind that we have a right-angled triangle we have $$\cos{\theta}=R/(R+H),$$ so $$s=R\cos^{-1}{(R/(R+H))}.$$ If $R$ is much larger than $H$ then the straight line distance to the horizon is approximately equal to $\sqrt{2HR}$, as we worked out in the article. Moreover, in this case the straight line distance is approximately equal to the walking distance over the Earth's surface. This gives that for $R>>H$ $$R\cos^{-1}(R/(R+H)) \approx \sqrt{2HR}.$$
Solution to problem 2: You see something, like a cloud or a hot air balloon, high in the sky beyond the horizon and you know its maximum possible height above the ground. Can you work out how far away it could be?
Let's assume that the object is at the maximum possible height $h$ above the surface of the Earth. So in our two-dimensional view it lies somewhere on the circle of radius $R+h$ about the centre $O$ of the Earth. Since it is beyond the horizon, the object lies beyond (from your point of view) the straight line through $O$ and the horizon point $P$. And since it is visible over the horizon, the object lies "above" the tangent line passing through your view point and the horizon point $P$. Thus the object lies somewhere on the arc of the circle between points $A$ and $B$ (see the diagram on the right).
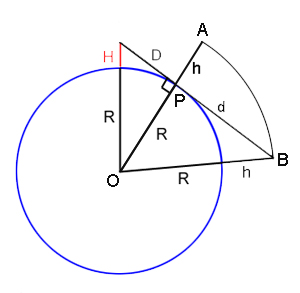
Using Pythagoras' theorem, we see that the distance from you to point $A$ is $$\sqrt{D^2+h^2}.$$ We have already worked out that for a person of height $H=1.8m$, we have $D=\sqrt{2RH}=4800m,$ and we know that $R=6400km.$ So for a maximum height of $h=2km$ we get that the object is at least $5.4km$ away from you.
Now let $d$ be the distance from $P$ to $B$. Using Pythagoras' theorem on the right-angled triangle $OPB$, we get $$d^2+R^2=(R+h)^2.$$ Noting that $R > > h$, so that we can ignore the $h^2$ term, we have $$d \approx \sqrt{2Rh}.$$ Now the maximum distance to the object from the observer is approximately equal to $$D+d=\sqrt{2HR}+\sqrt{2Rh}.$$ Using $D=\sqrt{2RH}=4800m$, $R=6400km,$and $h=2km$ we get that the maximum distance to the object is approximately $164.8km.$