We’ll show that
![\[ \frac{x}{10^7} = e^{-\left(\frac{y}{10^7}\right)}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0001.png) |
The point 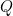 moves at a constant speed of
moves at a constant speed of 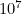 , so we have
, so we have 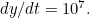 Since
Since 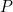 moves at a speed that is proportional to the distance
moves at a speed that is proportional to the distance  left to travel we have
left to travel we have 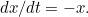 From this we see that
From this we see that
![\[ dy/dx = -\frac{10^7}{x}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0008.png) |
which gives
![\[ y = -10^7 \ln {cx}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0009.png) |
for some constant 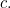
We can work out the value of  using our initial conditions. At the start, the point
using our initial conditions. At the start, the point 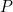 still needs to travel the whole length of the line segment
still needs to travel the whole length of the line segment 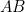 , which is
, which is 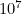 . Therefore
. Therefore 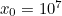 . The point
. The point 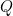 hasn’t gone anywhere yet, so
hasn’t gone anywhere yet, so 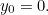
Plugging this into the expression above gives
![\[ 0 = -10^7 \ln {c10^7}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0015.png) |
so
![\[ e^0 = 1 = c10^7. \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0016.png) |
Therefore,
![\[ c = \frac{1}{10^7}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0017.png) |
so
![\[ y = -10^7 \ln {\frac{x}{10^7}}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0018.png) |
and
![\[ \frac{x}{10^7} = e^{-\left(\frac{y}{10^7}\right)}, \]](/MI/8474411310ebb19cf148f3ee0185d716/images/img-0001.png) |
which is what we wanted to show.