How is frequency related to pitch? That's a topic that's always fascinated me, as well as being rather fundamental to the practice of music! And it was one of the things that came up in my recent conversation on the Maths on the Move podcast, where we were discussing some of the many ways in which maths and music are connected.
A musical note’s pitch is described by the number of oscillations-per-second it exhibits as a sound wave. A sound wave is a pattern of waves through air, similar to the ripples in a pond. Except that ripples make the surface of the pond oscillate up and down, which would be at 90 degrees to the direction of travel of the waves, something called a transverse wave. Instead a sound wave oscillates the air by compressing and rarefacting the air in the same direction as the sound wave is travelling. Such waves are called longitudinal waves.
The frequency of any wave is measured in Hertz (Hz), which is the number of oscillations per second. Human hearing runs from extremely low notes of around 20Hz (20 oscillations per second) to the extremely high notes of around 20,000Hz, (20,000 oscillations per second). As our brains aren’t capable of perceiving each individual oscillation even at the lowest end of that range, we experience them as what we call pitch. For example, the orchestral tuning note of A above middle C is 440Hz. This means when strings, woodwind and pipes play an A, they are all generating soundwaves at a base rate of 440 per second.
Right. Let’s dive into some fun audio!
Pitch from clicks
Usually when you hear a note you are hearing a wave, the simplest of which is a sine wave. But as you'll see from this example, if you start with a simple series of clicks and increase the tempo of the clicks enough, we will begin to perceive the clicks as an ascending pitched tone.
The image shows the individual clicks at the start of the waveform (the far left), but by the end of the clip (the right), it’s blended into a blur of sound.
Exciting! At the beginning of this clip the clicks are occuring at a frequency of 4Hz – that’s four times a second. As our hearing range lies between 20Hz to 20,000Hz, a pure tone at 4Hz would, by definition, be inaudible, which is why I’ve used clicks rather than a sine wave.
By the end of the clip the tempo is 500 times faster, reaching about 2,000 clicks a second (2,000Hz). Because we can’t perceive 2,000 individual clicks per second, we hear this as a note we call B6 (just under three octaves above middle C on a piano).
The major drawback of this system of using clicks is that, unlike a sine wave, a click is very rich in harmonics (which is why they can be heard). So all those extra harmonics are interacting by the end of this audio clip, causing all manner of exciting overtones and overwhelmingly noisy artefacts – all the stuff that sounds like the Doctor’s Tardis! Quite a cool effect, but does weaken the perception of the pure tone somewhat.
However, hopefully the point is made: by starting with a series of clicks that can be heard individually, we can speed them up enough to become what we perceive as tones or notes – and we can no longer perceive the individual clicks! Just to re-iterate – the actual pitch of the clicks themselves is not changing, the same click is used throughout; literally all we are doing is increasing the rate at which they occur.
Whole Number Ratios
Now we’ve established that pitch can be thought of (and is) a series of oscillations at a given frequency – and those oscillations can be made by clicks as much as they can be made by sine waves – we can explore further this deep mathematical relationship that informs the very fundamental basis of all music.
This relationship is the whole number ratio. In the western tradition, the major and minor scales (and all modes, for that matter) are based on whole number ratios of frequencies. This also underpins a lot of world music too – it’s just a natural way we humans work with sound.
A whole number ratio is one that can be described with whole numbers in relationships such as 2:1 (which we read as "2 to 1"), 3:2, 4:3, 5:3, and so on. When we apply that idea to frequencies it means playing two frequencies with a whole number ratio. So a ratio of 2:1 could be two notes with the ratios 1000:500 (Hz) and 3:2 could be 600:200 (Hz).
This is fundamental to music because we can construct a major scale purely from a set of these wholetone ratios. (I’ve included the minor third in the table below, which is not part of the major scale, but is a whole number ratio as well):
| C | Unity | 1:1 |
| D | Whole tone | 9:8 |
| E♭ | Minor third | 6:5 |
| E | Major third | 5:4 |
| F | Fourth | 4:3 |
| G | Fifth | 3:2 |
| A | Major sixth | 5:3 |
| B | Major seventh | 15:8 |
| C' | Octave | 2:1 |
Let’s listen to how all this works in practice!
The octave (2:1)
When we consider the idea of playing clicks in a ratio of 2 to 1, we would need to play sets of clicks: where the first set has one click, the second set has two clicks played evenly over the same length of time. In the example below, I’ve presented these two sets happening alternately instead of at the same time because the slower clicks would be masked by the faster ones.
The octave (2:1) – Alternating sets of clicks are used in the audio sequence. The first set is played for the first two bars where there are 4 clicks per bar. The second set, which the clicks are twice as fast with 8 clicks per bar, plays for the second two bars, and so on.
At the start of the clip, they are playing slowly enough to hear that there are two sets of clicks, the fast clicks playing twice as fast as the slow clicks. (Yes, it sounds reminiscent of the famous drum intro of Blue Monday by New Order!)
The fun part is that once the tempo has been sped up (to 134Hz for the lower note and 268Hz for the higher note), the clicks blend together until we hear the two sets of clicks as basic notes an octave apart. Because the tempo is a bit lower than the first example, there are fewer artefacts, but is still fast enough for the effect to work.
A musical pattern of bouncing octaves was a very commonly used bassline in disco songs, so the end of the clip may sound kind of familiar too!
The fifth (3:2)
The fifth note of the scale can be generated with a frequency that is 1.5 times that of the root note – the frequencies of the notes have the ratio of 3:2. In the key of C, this fifth note is G, and is literally five steps up from C on the white notes of a piano keyboard.
(Image from Maths in a minute: Maths and music)
If we start with sets that are playing 3 clicks against 2 clicks we can hear something that is recognisable as a rhythm. (In musical terms it’s a triplet against duplets). This time the sets of 3 and 2 are playing together (not alternately as in the previous example) as they don’t completely overlap.
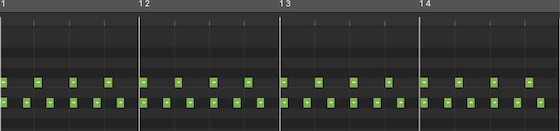
The fifth (3:2) – The image shows the sets of clicks played simultaneously in the audio sequence. The first set (shown in the top line) has 4 clicks per bar, is the root note. Below it is the second set with 6 clicks per bar, a ratio of (3:2) with the root note, creating the fifth note.
As we speed them up, they clearly diverge into two notes – the lower is the root note and the higher is the fifth. To make this slightly clearer at the end of the audio clip, I’ve soloed one and then the other so you can really hear there are two notes in there.
The fifth in action!
What I find delightful (and slightly mystical) is that you can start with just clicks playing what sounds like a simple rhythm, and by simply speeding it up (a lot), this one rhythm diverges into two discrete notes. But this is just how sound works – all sound is a mixture of sine-waves, all happening at the same time, in a constant flux. All we’re doing here is simplifying that to make it really apparent. Underlying that simple rhythm at the start of the clip are actually two streams of clicks at different rates, which eventually become perceivable as notes to our ears.
The major third (5:4) and the minor third (6:5)
The interval of a third is the basis of all western harmony: when combined with the root note and the fifth, it creates a complete chord known as a triad. It’s the start of harmony and our subsequent ability to construct chord sequences and complex harmony from the baroque period onwards. This was around 500 years ago in Europe, after a revolution in how scales were tuned (see the caveat below).
To create a major third we need to use the ratio of 5:4 – so 5 clicks played for the third note to every 4 clicks played for the root note:
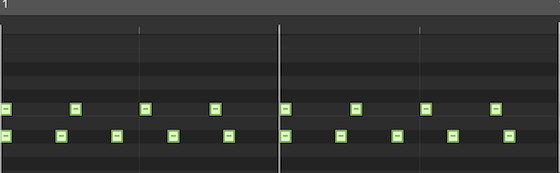
Major third (5:4) – The image shows the two sets of clicks needed to create a major third, repeated over two bars. The first set in the top line is the root note, and has 4 clicks per bar. The second set, for the major third above the root, has 5 clicks per bar.
Here's how it sounds:
The two sets of clicks building to a major third
The minor key version of the third (the minor third) is commonly thought to be the "sad" cousin to the "happy" sound of the major third, and it is created with the ratio of 6:5.
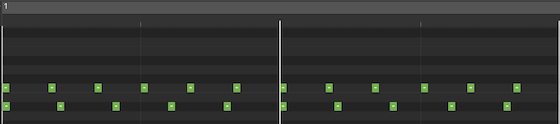
Minor third (6:5) – The image shows two bars of the sets of clicks needed to create a minor third. The first set in the top line is the root note, and has 5 clicks per bar. The second set, for the minor third above the root, has 6 clicks per bar.
And here's how the minor third emerges from these two sets of clicks:
The minor third
Our glorious finale – the major triad
So, now that we’ve demonstrated how the notes of the major and minor scales can be created from a set of whole number ratios, the crowning glory of this article will be to play not one, not two, but three ratios together all at the same time to create a major triad!
We will play three sets of clicks simultaneously – 4 clicks per bar for the root note, 6 clicks per bar for the fifth note and 5 clicks per bar for the major third, giving the ratio of 4:6:5.
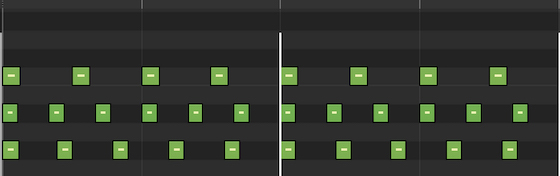
Major triad (4:6:5) – The three sets of clicks that create a major triad. The top line is the root note with 4 clicks per bar. The middle line is the fifth note with 6 clicks per bar – this is in a ratio of 3:2 to the root note. And the bottom line is the major third with 5 clicks per bar – a ratio of 5:4 with the root note.
And here's how it sounds:
The major chord
Yes, before your very ears, a lumpy sounding rhythm made of exactly the same clicky noise will miraculously transform into a beautiful major chord, the starting point of all western harmony!
Ok, so it’s a bit grainy, but the essence is certainly there. Remember, the "graininess" is because we’re using clicks not sine waves (or even smoother synth tones like the sawtooth or triangle waves). Those clicks have plenty of their own harmonic content and that all gets mixed in to create a much richer sound than pure sine waves would.
Important Caveat
Everything I’ve written above is wrong! Well, not wrong, but since the late 1600s the use of whole tone ratios (known as just intonation) is not actually how we’ve been constructing the musical scale or to tune our musical instruments. What we have is very close to this, but it was realised it had to be calculated differently to enable scales that work in all the different keys.
To cut a long story short, if you construct a perfect scale from whole number ratios, that one key will be beautiful but you won’t be able to move (or modulate) to any of the other keys. (You can read more in my article Sine language.) This was solved (using maths!) first in China in the late 1600s by Zhu Zaiya, and around the same by several others in Europe, including Simon Stevin.
The solution, which we use to this day, is to average out the distance between each semitone to the 12th root of 2 (because there are 12 intervals in an octave). The result is that the only true wholetone ratio remaining is the octave (2:1). We call it equal temperament, or 12-tone equal temperament, or even 12-TET, because there are other x-TETs out there! Whatever we call it – it has enabled the whole world of harmony to be opened up in a way not previously possible. And of course, it is all entirely based on clicks – just very fast ones!
About the author

Oli Freke is a London-based musician and composer who’s recently published the definitive guide to synthesizers, Synth Evolution: From Analogue to Digital (and Back) on Velocity Press. He’s also supported the Human League on tour, composed music for TV and had club chart success over the course of twenty years in the music industry.
Comments
wonderful examples! -- and what (in detail) are the "clicks"?
awesome cool -- many thanks! -- and a quick question: what specific waveform did you use for the "clicks"? -- i.e., how many cycles, of what shape? -- square waves, triangles, ...??
Thanks Mark - good question!…
Thanks Mark - good question! I actually just used a really simple rimshot sample as it's short sound with a good transient. But your question does make me wonder if an even better sample would have been a square wave with fewest number of cycles still audible as a single click...I'm going to have to investigate now! :-)
On musical scales.
Very good, very clear, very interesting. Thank you.
Math and music frequency
My wife thinks I’m crazy. I am 76 and a lover and teacher of math my whole life.
My mind was totally blown reading this article and listening to the audio you produced. I have NEVER even begun to think about this connection. I am fascinated by geometry but this has genuinely intrigued me.
Thank you for sharing.