
This article is part of the Researching the unknown project, a collaboration with researchers from Queen Mary University of London, bringing you the latest research on the forefront of physics. Click here to read more articles from the project.

The six-sided prisms of mineral quartz. (Image by Didier Descouens)
Oxides – materials that contain oxygen as well as other elements – are all around us. Most stones and rocks are oxides, as are many of the materials used in technology, even the window glass as you gaze outside at the spring sunshine.
Many oxides consist of a metal cation (a positively charged ion formed when an atom loses electrons) surrounded by a certain number of oxygen atoms (depending how many free electrons the metal has). For example silicon will have four oxygens atoms around it, forming a tetrahedron with the silicon atom at the centre. These tetrahedra then connect to each other at the corners: "Every tetrahedron in this network is connected to four others, but there's such flexibility that you can join these up in all sorts of different ways," says Martin Dove, Director of the Centre for Condensed Matter and Materials Physics at Queen Mary University of London. They might form rings of, say, six or eight tetrahedra, or some other three dimensional structure. The structure might be essentially random, like window glass, or highly ordered like mineral quartz with its six-sided prisms.
And although we think of these structures, such as rocks, as being very hard and rigid, they can actually move and flex, but only in very specific ways. It takes an awful lot of energy to stretch or shrink the molecular bonds within the molecules so the tetrahedral units that make up the oxide crystals stay very rigid. But there is some flexibility in the connection between the corner of one tetrahedron and another, so that the overall structure may be free to rotate and flex at the corners, leaving the rigid tetrahedrons unchanged.
Freedom versus constraints
Analysing the rigidity of such a structure is surprisingly simple: it is essentially a counting exercise of the ways the elements in the structure can move and the constraints against this movement. Any rigid object in three dimesions can move in six ways. It can move left-right, up-down and forward-back, and it can rotate in three directions too, called the roll, pitch and yaw (in the language of sea captains), each rotating around one of three perpendicular axes. Together these are called the object's degrees of freedom: any movement can be described as a combination of these six types of motion.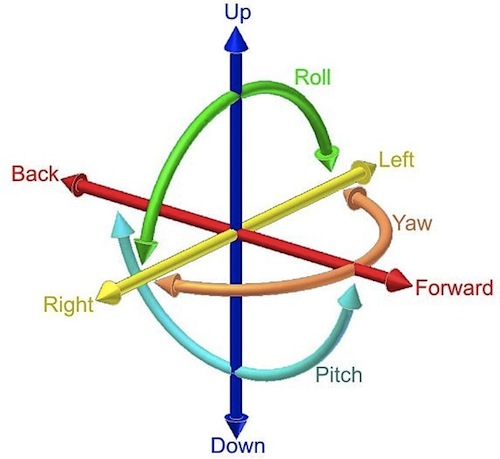
The six degrees of freedom of a rigid object
Individually, the rigid tetrahedra in silica crystals each have six degrees of freedom. But they are not alone, they are constrained by their connections to all the other tetrahdra in the network. The corner of one tetrahedron is joined to the corner of another, meaning both corners must have the same x, y and z coordinates. These three shared coordinates give us three constraint equations for those two corners (say, if the corners of two tetrahedra are joined at the point (1,2,3), this gives the three constraint equations x=1, y=2 and z=3), equating to 3/2 constraints for each corner of each tetrahedra. Each tetrahedron has four corners, so each tetrahedron is constrained by 3/2 x 4 = 6 constraint equations in total.
Any network of tetrahedra is exactly on the balance between being over-constrained and under-constrained. "There's an exact balance between the constraints and the degrees of freedom," says Dove. "If it was over-constrained, the whole thing would be rigid and unmoveable. If it was under-constrained, it would be floppy and just wobble around like jelly. But it turns out that it's exactly on the balance."
A network of tetrahedra making up silica – click on the image to see a movie showing the motion in this material. (Movie produced by Min Gao and Martin Dove at QMUL.)
This delicate balance puts materials made of networked tetrahedra, such as the silica and other similar oxides, in an interesting position. If the symmetries of the structure make some of the constraints redundant, the balance shifts from rigidity to flexibility in the material, and very specific types of motion becomes possible.
This flexibility allows the material to vibrate in certain ways, called rigid unit modes or RUMs, as the rigid tetrahedra flex back and forth at the corners in these allowed directions. And as the tetrahedrons are connected in a large network, the movement of one pulls the other, causing a wave to pass through the network.
The right place at the right time
It was being in the right place at the right time that lead Dove to develop RUMs as a way of investigating materials made up of networked tetrahedra. After initial research as part of a physics department, he moved to theoretical chemistry in 1984, studying the dynamics of molecules at the University of Cambridge. When molecules vibrate in a crystal, some of the vibrations move the molecules closer and further apart. "You can imagine you've got these molecules lined up and a wave going through the system making them dance together in some way."
A few years later Dove was recruited to the Department of Earth Sciences where people were already using models of rigid tetrahedra to try to explain various properties of materials. Of particular interest to the researchers there was the question of where phase transitions come from, when a material changes form, such as water changing from ice, to liquid, to steam as it is heated. "They realised that the materials that make up the Earth all underwent phase transitions, and they wanted some input from physics. I guess the little flash of insight was to say, this surely is a problem in the theory of vibrations of molecules. All I have to do is connect my molecules and I've got everything lined up ready to go." And here is where the pieces all fell into place: although this was not the obvious approach for the many people working in silicates at the time, it made great sense to Dove as he was coming from outside of the field.
Dove adapted the software he'd originally developed to study the vibrations of individual molecules in crystals, but now used it to examine the network of molecules joined together at the corners. This, he says was his key contribution: tools that could make the analysis much easier. People had done this rigidity versus flexibility analysis before, but it had required a huge effort. "One person had done an analysis on one material, but that was as far as it got." Dove's software could quickly analyse any structure, giving an explicit count of how flexible any such material was. "What we then had was a tool that allowed us to very quickly work through a range of materials and then start to see the bigger picture."
The hidden flexibility in these network materials, revealed by the counting arguments behind Dove's software, underpins a lot of their properties. Initially Dove used the RUMs of a material to explain why and when phase transitions occurred. In particular, the temperature at which these materials changed phase was related to the frequency of the vibration modes: it is the product of the frequency of the vibration mode and a measure of the stiffness of the tetrahedra.
Shrinking in the heat and softening in the squeeze
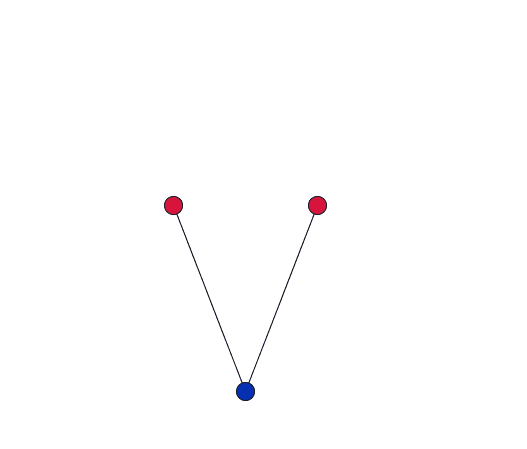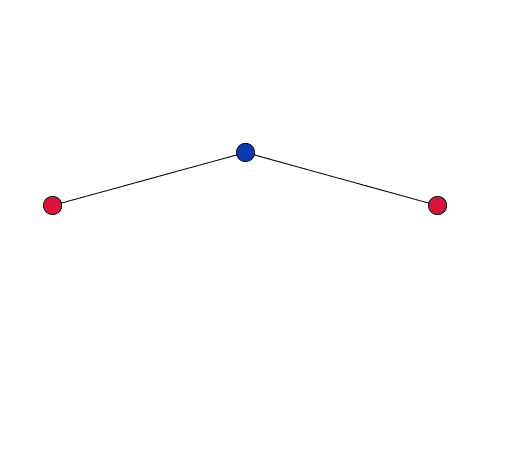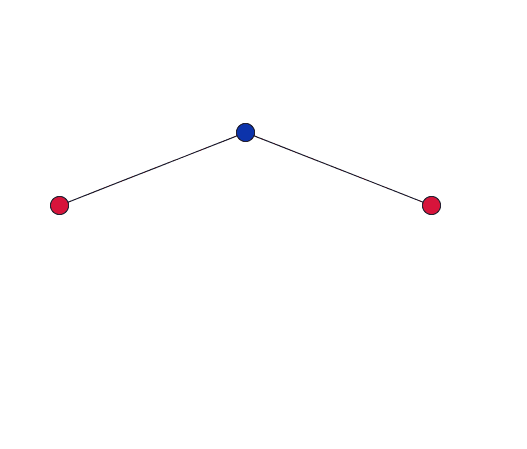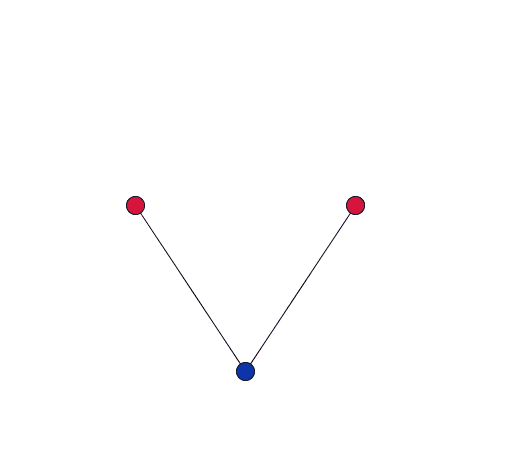
As the blue oxygen atom, shared by two cations in the network, vibrates, it pulls the red cations together.
RUMs also held the key to explaining another, surprising, property of some materials, called negative thermal expansion. "Most materials expand when you heat them up. Everyone gets taught that they expand and people use that expansion as an explanation for why pipes get stuck together, roads crack and things like that. But some materials have a very strange property: they shrink when you heat them up."
Dove gives a simplified explanation of the role of RUMS in this property. Imagine two cations, each at the centre of a tetrahedron, connected by stiff bonds to a shared oxygen atom. As the network vibrates, the shared oxygen atom swings backward and forward – as in the movies to the right. "This vibration gets bigger as you heat the material up. But because the bonds are stiff – they are all a fixed length – the movement [of the oxygen atom] necessarily pulls the cations in."
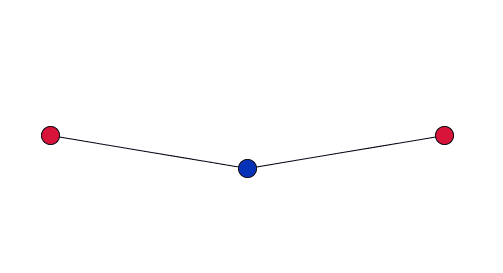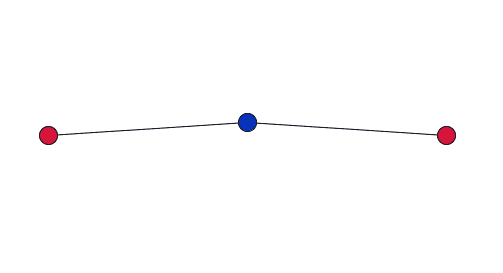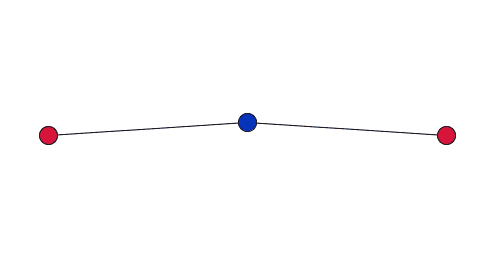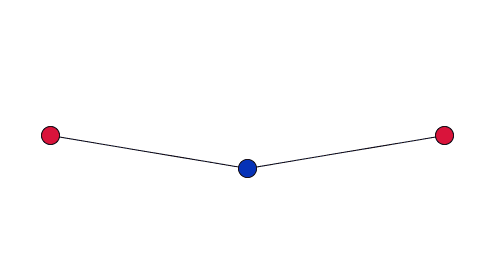
If the vibration only has a small amplitude, the red cations barely move.
When the amplitude of the vibration is small, and the oxygen atoms move through only a short distance, the cations will barely move. But as the amplitude of the vibration increases, the cations will be drawn in by a much larger distance. So in order for this to be significant you are only interested in vibrations with a large amplitude where the atoms move a relatively large distance.
The amplitude of the vibration is inversely proportional to the square of the frequency of the vibration:
![\[ \mbox{amplitude}=\frac{1}{\mbox{frequency}^2} \]](/MI/7cdd585868e91c576209c5101d994051/images/img-0001.png) |
In the last two years, since Dove moved to the Queen Mary, he has been working on how negative thermal expansion relates to a surprising new property. "Since I've been here we've discovered that some materials get softer when you squash them. That's very counter-intuitive because when you squash something, the atoms get pushed tighter and you expect it to get stiffer."
Dove and his colleagues knew that some examples of these materials also had negative thermal expansion, so in a recent paper they posed the question: does this property of things getting softer when you squash them (called pressure induced softening) follow as an automatic consequence of negative thermal expansion? Some of the materials they have been investigating are zeolites, very porous materials with great big channels through them, like molecular sieves. They are used in washing detergents as the dirt gets trapped in the channels of the zeolite and together they are washed out of your clothes with the water. "Many of these zeolites had negative thermal expansion. And of all those that did, all of them got softer when you squashed them."
The zeolites results are good evidence that their hypothesis is correct. But now they need a theoretical understanding of this connection. Dove and his colleagues are beginning to develop this using mathematical models based on RUMs. "We have a little one-dimensional model that you can put your equations in, of what the relevant forces are, and make all this work," says Dove. This model is like a framework of rods, where you have two atoms joined in a rod instead of a tetrahedron. Negative thermal expansion happens instantaneously in these models when there is a balance between the degrees of freedom and constraints, and it turns out that pressure induced softening also emerges as a necessary consequence. Now they have proved their theory in one dimension, they are working on the next step: a proof in three dimensions.
Connections are key
It's the connections between the rigid tetrahedral units of these materials that underpins their properties. And it is the connection between different areas of science that has helped understand them. "Different communities of scientists will have different ways of thinking about something," Dove says. It was his movement between physics, chemistry and geoscience that connected up the different knowledge in these areas."Sometimes it's an outsider view that actually creates a new way of thinking."
Dove believes it was his different perspective on the problem that helped him find the answer. For example, rather than thinking about the physical picture of atoms and molecules, he was used to thinking of how waves moved through crystal structures. This different way of thinking was the key to understanding how the networks of rigid tetrahedra could explain their properties. "I don't think what we do is particularly clever, nevertheless, not many people would have lined up these pieces together. I think that's how sometimes things happen; you come into something, you think about it in a different way, realise that what looks like a difficult problem is something you can actually do.”
About this article

Martin Dove is the Director of the Centre for Condensed Matter and Materials Physics at Queen Mary University of London.
Rachel Thomas, Editor of Plus, interviewed Martin Dove in London in January 2014.