Suppose we have 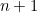 control points
control points 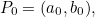
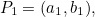 ...
... 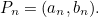 We will represent the corresponding Bézier curve by points
We will represent the corresponding Bézier curve by points 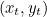 where
where 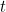 runs from 0 to 1. In other words, for each
runs from 0 to 1. In other words, for each 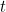 between 0 and 1 we get a point
between 0 and 1 we get a point 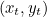 and together these points form the curve. The formulae for
and together these points form the curve. The formulae for 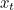 and
and 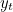 are
are
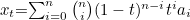 |
|||
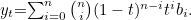 |
where
![\[ { n \choose i} = \frac{n!}{ (n-i)! i!} \]](/MI/86ba754dffbb5632e39e480c038316a9/images/img-0012.png) |