On 12 June the World Cup kicks off in Brazil where 32 teams will compete for the greatest prize in football. A total of 64 games will be played up to the Final and much skill will be displayed by the game's elite players. Can science add anything to the mix? The complexity of ninety minutes' play rules out any possibility of simulating an entire game; but there are some events which are so fleeting and where the intentions of the players are so specific, that scientific analysis can be fruitful.
One such is the swerving free kick. A striker is intent on scoring a goal, a line of defenders (the wall) is set up to block his shot and the goalkeeper will try to save anything that gets through. Everything is over in a second or less. So the free kick is really a drama, a "game within the game" and coaches often refer to it as a "set play". I'll try to show how this drama plays out in practice — but first, let's meet the cast!
The ball

Figure 1: The Brazuca has six panels. Image with thanks to John Moore Sports, Bath
The first truly modern football, the 32-panel hexagon/pentagon pattern was introduced at the World Cup of 1970. This format lasted nearly four decades but in 2006 a radical new design burst onto the scene. This ball, the Teamgeist, had 14 panels. The trend continued and its successor in 2010, the Jabulani, had only eight. As I argued in this Plus article, reducing panel numbers was not perhaps the cleverest design objective. A degree of surface roughness is necessary to ensure aerodynamic stability, something which occurs naturally with the high panel density of the 32-panel ball. The 2014 World Cup ball, the Brazuca, has only six panels (see figure 1) and so artificial surface roughening is a must. This is achieved by a microstructure of fine pimples, clearly visible in the image. The objective is to avoid the kind of chaotic flight movement called knuckling which sometimes occurred with the Teamgeist and Jabulani balls, a behaviour which drove goalkeepers to distraction.
The striker
Just about anyone can wallop a football but an elite free-kicker must do so much more to ensure a successful outcome. To defeat an agile goalkeeper the ball must be kicked with pace and controlled spin. Add the fact that the striker is also trying to swerve the ball over the defensive wall and it's not difficult to see why so few free kicks are converted in practice. A success rate of between 5% and 10% is common; compare this with the figure for penalty kicks of around 80%.
The ball's initial speed following a kick is easily derived from a simple model. By considering the masses and speeds of the striker's foot and the ball before and after impact it's possible to show that the ball's release speed is given by
![\[ v_ b = v_ f\frac{(1+e)}{(1-\frac{m_ b}{m_ f}e)}. \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; (1) \]](/MI/c90b10b741540b7996439332fac50b18/images/img-0001.png) |
In this equation, 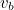 and
and 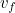 are the ball and foot speeds and
are the ball and foot speeds and 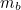 and
and 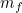 the respective masses. The parameter
the respective masses. The parameter  is the coefficient of restitution. It gives a measure of the energy conserved when bodies collide, and because energy is always lost in practice, measured
is the coefficient of restitution. It gives a measure of the energy conserved when bodies collide, and because energy is always lost in practice, measured  -values are always less than 1. Such collisions are described as inelastic. In a free kick, where foot and ball both deform during the impact,
-values are always less than 1. Such collisions are described as inelastic. In a free kick, where foot and ball both deform during the impact,  -values around 0.5 would be expected. The equation has an interesting implication, however. For a perfectly elastic impact (
-values around 0.5 would be expected. The equation has an interesting implication, however. For a perfectly elastic impact (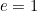 ) and for a very massive kicking foot (say
) and for a very massive kicking foot (say 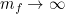 ) we have
) we have 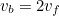 . So you’ll never kick a ball at more than twice the speed at which you can swing your leg! In the real world, ball speeds up to 30 metres per second are easily achieved for practical
. So you’ll never kick a ball at more than twice the speed at which you can swing your leg! In the real world, ball speeds up to 30 metres per second are easily achieved for practical  -values around 0.5.
-values around 0.5.
What about spin? The simple model above assumes that the impulse of the kick passes exactly through the ball's centre of mass. To spin the ball the point of impact should be slightly to the side: in other words there must be an offset between the line of the impulse and the ball's centre. This leads to a trade-off, as too much applied spin is detrimental to forward speed. In practice spin rates of 600 rpm can easily be achieved with ball speeds around 30 metres per second. It's interesting to note that, unlike the ball's forward speed, which is considerably reduced by aerodynamic drag, spin is scarcely affected over the typical flight time of a free kick, about one second in practice.
The defensive wall
The defensive wall is almost as old as the game of football itself. Its sole purpose is to prevent a free shot at goal — figure 2 shows the general set-up. A line of defenders stands 10 yards (9.14m) from the striker. Goalies generally arrange the wall so that between two thirds and three quarters of the goal line is protected. In theory this should leave the goalie, positioned as shown in figure 2, with a clear view of the shot, but members of the attacking side invariably join the wall to frustrate this intention by blocking his view.
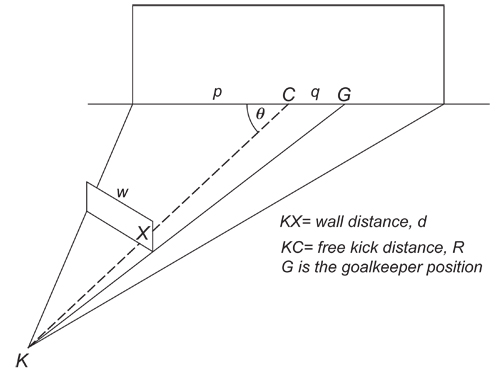
Figure 2: The geometry of defensive wall position.
A little thought reveals that the size of the wall should reduce as the angle of the kick, 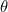 in figure 2, becomes more acute (that is, as point
in figure 2, becomes more acute (that is, as point 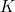 moves away from the centre of the goal towards the sides). And whilst goalies use much practical insight in setting the wall, a little mathematics can help. It’s not too difficult to show using the geometry of figure 2 that the required wall width,
moves away from the centre of the goal towards the sides). And whilst goalies use much practical insight in setting the wall, a little mathematics can help. It’s not too difficult to show using the geometry of figure 2 that the required wall width, 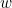 , for any position of the shot
, for any position of the shot 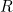 , is given by
, is given by
![\[ w(\theta , R) = d \sin {\theta }\left(\frac{p}{R-p\cos {\theta }} + \frac{q}{R+q\cos {\theta }}\right).\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; (2) \]](/MI/a2ba708bc2a99eaff83699c8ee6d6bfa/images/img-0005.png) |
In this equation 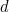 is the mandatory 10-yard distance of the wall from the striker and the width of the goal is
is the mandatory 10-yard distance of the wall from the striker and the width of the goal is 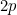 (8 yards or 7.32m). The parameter
(8 yards or 7.32m). The parameter 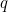 describes how well the wall protects the goal line. As figure 2 indicates, the portion of the goal line covered is
describes how well the wall protects the goal line. As figure 2 indicates, the portion of the goal line covered is 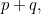 so since the length of the goal line is
so since the length of the goal line is 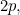 the proportion covered is
the proportion covered is 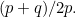 For example,
For example, 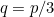 would imply two thirds of the goal line was covered; the figure for
would imply two thirds of the goal line was covered; the figure for 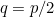 is three quarters.
is three quarters.
Figure 3 shows the number of defenders required for various free kick distances and angles. This number is easily obtained by dividing the wall width 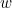 in the above equation by the average spacing of defenders in the wall, say 0.45m. Central free kicks, as might be expected, are the most dangerous and five or even six-defender walls are not uncommon close to goal.
in the above equation by the average spacing of defenders in the wall, say 0.45m. Central free kicks, as might be expected, are the most dangerous and five or even six-defender walls are not uncommon close to goal.
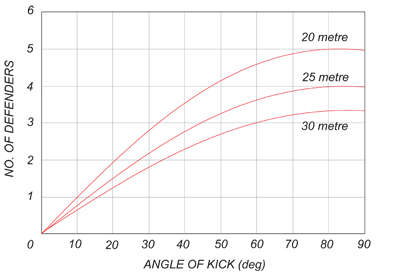
Figure 3: The number of defenders required in defensive wall.
The goalkeeper
Today's elite goalies, male or female, are very tall and agile leading to a very obvious question: just how much of the goal is technically covered in a diving save? We set out to answer this question at the University of Bath by filming a series of attempted saves using high-speed digital cameras. Figure 4 shows the diving envelope — the goalie's maximum reach in a finger-tip save, which leads in turn to the concept of an unsaveable zone. These are the locations where a sufficiently speedy and accurate shot should ensure success.
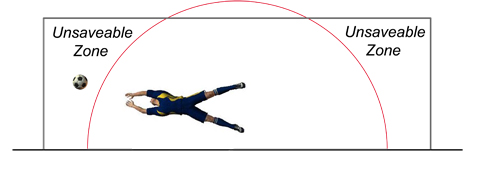
Figure 4: The diving envelope and the unsaveable zone
Lab measurements using professional goalies suggest that the unsaveable zone represents about 30% of the goal area and that shots played within it should never be saved. Data from actual matches show success rates for penalties somewhat better than 80%, however, and this is because goalies can move, quite legally, before the ball is kicked. Weak shots are easily gobbled up despite apparently perfect placement by the striker. Much depends on how well the goalie reads the intended direction of the shot, and how quickly a save can be executed. Reaction times and speed of dive are vitally important, especially in a free kick where a clear view of the shot and the ball's movement in flight are not guaranteed.
Lights, camera, action!
Now that we’ve met the cast our little drama can begin. A free kick has been awarded in a central position (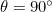 in figure 2), exactly 22m from goal. This a prime location for scoring with free kicks.
in figure 2), exactly 22m from goal. This a prime location for scoring with free kicks.
The striker places the ball on the ground and the referee pushes the defenders away. He strides ten paces forward to show where the wall should be. The goalie frantically aligns one edge of the wall with the far goalpost, as in figure 2, and four defenders join the wall. Our second equation suggests that, aiming for a coverage of two thirds of the goal line, this is half-a-defender light for a shot from this position, but goalies value experience more than mathematics (we leave the calculation to you). Of course, players from the attacking side join the wall to block the goalie's view of the shot.
After a moment or two everything settles down. The referee blows the whistle; the ball cringes as the striker begins his run-up and all the players in the wall steel themselves against a possible impact from the ball. The goalie strains to see above the wall for his first sight of the ball and the thump as boot meets ball can be heard all over the now-silent ground.
What happens over the next second or so can be read in part 2 of this article.
About the author

Ken Bray is a theoretical physicist and a Senior Visiting Fellow in the Faculty of Engineering and Design at the University of Bath, UK. He has made a special study of the mathematics of football and the factors affecting the ball's flight, and has lectured, broadcast and published widely for both academic and general audiences. He has gone on record as saying that as much as 30% of a footballer's technique is down to an intuitive understanding of maths and science (although they shouldn't go anywhere near a computer!).
His book How to score: Science and the beautiful game has been reviewed in Plus. The author gratefully acknowledges provision of the experimental ball launching machine by the BOLA company of Cotham in Bristol.
Comments
Defensive wall
Hi Ken,
I am so impressed by the way you displayed the mathematics behind the free kick and it intrigued me to model a soccer free kick using your referring to your article.
However, I am struggling at proving the geometrical modelling of the defensive wall. May you please explain how did you come to that model? It will be greatly appreciated from you
Thank you so much for this article!
Regards
Defensive wall
Thanks Osama. Apologies for this delayed reply but I haven’t looked at the article for some time. I’ll dig out the maths and forward to you.
Ken
Geometry of the Defensive
Following the comment of Osama,
I am similarly struggling with proving the geometry of the defensive wall
Could you help us?