
Infinity or -1/12?
Recently a very strange result has been making the rounds. It says that when you add up all the natural numbers
1+2+3+4+...
then the answer to this sum is -1/12. The idea featured in a Numberphile video (see below), which claims to prove the result and also says that it's used all over the place in physics. People found the idea so astounding that it even made it into the New York Times. So what does this all mean?
The maths
First of all, the infinite sum of all the natural number is not equal to -1/12. You can easily convince yourself of this by tapping into your calculator the partial sums
$$S_1 = 1$$ $$S_2 = 1+2 = 3$$ $$S_3 = 1+2+3=6$$ $$S_4 = 1+2+3+4=10$$ $$...$$ $$S_n = 1+2+3+4+ ... +n,$$ and so on. The $S_n$ get larger and larger the larger $n$ gets, that is, the more natural numbers you include. In fact, you can make $S_n$ as large as you like by choosing $n$ large enough. For example, for $n=1000$ you get $$S_n = 500,500,$$ and for $n = 100,000$ you get $$S_n = 5,000,050,000.$$ This is why mathematicians say that the sum $$1+2+3+4+ ... $$ diverges to infinity. Or, to put it more loosely, that the sum is equal to infinity.

Srinivasa Ramanujan
So where does the -1/12 come from? The wrong result actually appeared in the work of the famous Indian mathematician Srinivasa Ramanujan in 1913 (see this article for more information). But Ramanujan knew what he was doing and had a reason for writing it down. He had been working on what is called the Euler zeta function. To understand what that is, first consider the infinite sum
$$S = 1+1/4+1/9+1/16+ ... .$$ You might recognise this as the sum you get when you take each natural number, square it, and then take the reciprocal: $$S = 1+1/2^2+1/3^2+1/4^2... .$$ Now this sum does not diverge. If you take the sequence of partial sums as we did above,
$$S_1 = 1$$ $$S_2 = 1+1/2^2 = 5/4=1.25$$ $$S_3 = 1+1/2^2+1/3^2 = 49/36 = 1.361...$$ $$...$$ $$S_n =1+1/2^2+1/3^2 + ... + 1/n^2,$$
then the results you get get arbitrarily close, without ever exceeding, the number $\pi^2/6 = 1.644934... .$ Mathematicians say the sum converges to $\pi^2/6$, or more loosely, that it equals $\pi^2/6.$ Now what happens when instead of raising those natural numbers in the denominator to the power of 2, you raise it to some other power $x$? It turns out that the corresponding sum $$S(x) = 1+1/2^x+1/3^x+1/4^x... $$ converges to a finite value as long as the power $x$ is a number greater than $1$. For every $x > 1$, the expression $S(x)$ has a well-defined, finite value. $S(x)$ is what's called a function, and it's called the Euler zeta function after the prolific 18th century mathematician Leonhard Euler. So far, so good. But what happens when you plug in a value of $x$ that is less than 1? For example, what if you plug in $x=-1$? Let's see. $$ S(-1) = 1+1/2^{-1}+1/3^{-1}+1/4^{-1}... $$ $$ = 1+2+3+4+ ... .$$ So you recover our original sum, which, as we know, diverges. The same is true for any other values of $x$ less than or equal to 1: the sum diverges.
Extending the Euler zeta function
As it stands the Euler zeta function S(x) is defined for real numbers x that are greater than 1. The real numbers are part of a larger family of numbers called the complex numbers. And while the real numbers correspond to all the points along an infinitely long line, the complex numbers correspond to all the points on a plane, containing the real number line. That plane is called the complex plane. Just as you can define functions that take real numbers as input you can define functions that take complex numbers as input.
One amazing thing about functions of complex numbers is that if you know the function sufficiently well for some set of inputs, then (up to some technical details) you can know the value of the function everywhere else on the complex plane. This method of extending the definition of a function is known as analytic continuation. The Euler zeta function is defined for real numbers greater than 1. Since real numbers are also complex numbers, we can regard it as a complex function and then apply analytic continuation to get a new function, defined on the whole plane but agreeing with the Euler zeta function for real numbers greater than 1. That's the Riemann zeta function.
But there is also another thing you can do. Using some high-powered mathematics (known as complex analysis, see the box) there is a way of extending the definition of the Euler zeta function to numbers $x$ less than or equal to 1 in a way that gives you finite values. In other words, there is a way of defining a new function, call it $\zeta(x),$ so that for $x>1$ $$\zeta(x) = S(x) = 1+1/2^x+1/3^x+1/4^x...,$$ and for $x\leq 1$ the function $\zeta(x)$ has well-defined, finite values. This method of extension is called analytic continuation and the new function you get is called the Riemann zeta function, after the 19th cenury mathematician Bernhard Riemann. (Making this new function give you finite values for $x \leq -1$ involves cleverly subtracting another divergent sum, so that the infinity from the first divergent sum minus the infinity from the second divergent sum gives you something finite.) OK. So now we have a function $\zeta(s)$ that agrees with Euler's zeta function $S(x)$ when you plug in values $x>1$. When you plug in values $x \leq 1$, the zeta function gives you a finite output. What value do you get when you plug $x=-1$ into the zeta function? You've guessed it: $$\zeta(-1)=-1/12.$$ If you now make the mistake of believing that $\zeta(x) = S(x)$ for $x=-1$, then you get the (wrong) expression $$S(-1) = 1+2+3+4+ ... = \zeta(-1) = -1/12.$$ This is one way of making sense of Ramanujan's mysterious expression.
The trick
So how did the people in the Numberphile video "prove" that the natural numbers all add up to -1/12? The real answer is that they didn't. Watching the video is like watching a magician and trying to spot them slipping the rabbit into the hat. Step one of the "proof" tries to persuade you of something rather silly, namely that the infinite sum $$1-1+1-1+1-....$$ is equal to $1/2.$ The video doesn't dwell long on this and seems to imply it's obvious. But let's look at it a little closer to see if it makes sense at all. Suppose that the sum $1-1+1-1+1-1....$ has a finite value and call it $Z$. Adding $Z$ to itself you get the infinite sum $$Z+Z = 1-1+1-1+1-....+1-1+1-1+1-... .$$ But this is just the original sum, implying $$Z+Z=2Z = Z.$$ Since $Z=1/2,$ it follows that $1/2=1,$ which is nonsense. So the assertion that the infinite sum $1-1+1-1+1-....$ can be taken to equal to 1/2 is not correct. In fact, you can derive all sorts of results messing around with infinite sums that diverge (see here). It's a trick!
The physics
But how did this curious, wrong result make it into a physics textbook, as shown in the video? Here is where things really get interesting. Suppose you take two conducting metallic plates and arrange them in a vacuum so that they are parallel to each other. According to classical physics, there shouldn't be any net force acting between the two plates.
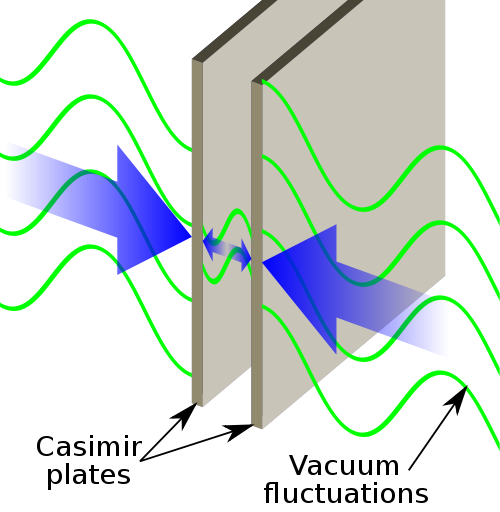
Illustration of the Casimir effect. Image: Emok.
But classical physics doesn't reckon with the weird effects you see when you look at the world at very small scales. To do that, you need quantum physics, which tells us many very strange things. One of them is that the vacuum isn't empty, but seething with activity. So-called virtual particles pop in and out of existence all the time. This activity gives a so called zero point energy: the lowest energy something can have is never zero (see here for more detail).
When you try to calculate the total energy density between the two plates using the mathematics of quantum physics, you get the infinite sum
$$1 + 8 + 27 + 64 +... .$$ This infinite sum is also what you get when you plug the value $x=-3$ into the Euler zeta function: $$S(-3) = 1 + 1/2^{-3} + 1/3^{-3} + 1/4^{-3} + ... = 1+ 8 + 27 + 64 +... .$$ That's unfortunate, because the sum diverges (it does so even quicker than than $S(-1)$), which would imply an infinite energy density. That's obviously nonsense. But what if you cheekily assume that the infinite sum equals the Riemann zeta function, rather than the Euler zeta function, evaluated at $x=-3$? Well, then you get a finite energy density. That means there should be an attractive force between the metallic plates, which also seems ludicrous, since classical physics suggests there should be no force. But here's the surprise. When physicists made the experiment they found that the force did exist — and it corresponded to an energy density exactly equal to $\zeta(-3)$!
This surprising physical result is known as the Casimir effect, after the Dutch physicist Hendrik Casimir.
Take a moment to take this in. Quantum physics says the energy density should be $$S(-3) = 1+8+27+64+... .$$ That's nonsense, but experiments show that if you (wrongly) regard this sum as the zeta function $\zeta(x)$ evaluated at $x=-3$, you get the correct answer. So it seems that nature has followed the ideas we explained above. It extended the Euler zeta function to include values for $x$ that are less than 1, by cleverly subtracting infinity, and so came up with a finite value. That's remarkable! The reason why we see $\zeta(-1)$ and $S(-1)$ in the Numberphile video and the physics textbook, rather than $\zeta(-3)$ and $S(-3),$ is that when you imagine the Casimir effect as happening in one dimension (along a line rather than in 3D), the energy density you calculate is $\zeta(-1)$ rather than $\zeta(-3)$.
So why did the Numberphile people publicise this strange "result"? They certainly know about the analytic continuation that makes the function well-defined, but that was something that was a little too technical for their video. Knowing they had the analytic continuation method, that would make the final result OK, hidden in their back pocket, they went ahead with their sleight of hand. In doing so they got over a million hits and had the world talking about zeta functions and mathematics. For this they should be congratulated. The mathematics of zeta functions is fantastic and what we described here is just the start of a long list of amazing mathematical properties. In bringing mathematics and physics to the public we always have to make choices about what we leave out and what we explain. Where to draw that line is something we all have to leave to our consciences.
About the authors

David Berman is a Reader in Theoretical Physics at Queen Mary, University of London. He previously spent time at the universities of Manchester, Brussels, Durham, Utrecht, Groningen, Jerusalem and Cambridge as well as a year at CERN in Geneva. His interests outside of physics include football, music and theatre and the arts.
Marianne Freiberger is editor of Plus.
Comments
Anonymous
I appreciate this piece, and it's helped me make sense of a lot of what's going on here. However, I have to part ways in calling for the Numberphile folks to be "congratulated." As a math teacher, and one who struggles every day to counter the deeply-ingrained notion that math makes no sense whatsoever, I can't stand it when that notion is spread across a wide audience and further ingrained into our culture. Sure, those who are already somewhat mathematically inclined are intrigued and want to know more. But those who are not see a video like this and say to themselves, "Further confirmation that math makes absolutely no sense." So I'm not about to congratulate them.
Matt E.
Sharon, MA
berman
Thank you for your comments, its something that many math teachers have expressed to me including lecturers at university which is what prompted us to write the piece; Its clear to me where I would draw the moral line and it isn't in the same place they have .
Anonymous
Well, I think the Numberphile guys made an entertaining video and I wish that my school maths teachers had been even half as good with their explanations as these guys are. For me it was the teachers, with their leaps of faith, blasting through the set books and omitting whole chapters (homework : study chapter so and so and do the exercises) who instilled the fear of maths and a sense of futility into all but the three or four kids, out of a class of 25, who could figure out what was going on. Maths teachers take a look in the mirror!
Nick
Berlin, Germany
Anonymous
Isn't it more important to recognise that maths is about adventure, discovery, fun? This is simply an example of an important aspect of in mathematics - you take some concept, abstract it and extend it, and see where it leads. Shouldn't more maths teaching and learning emphasise this?
A nice example that I use in my classroom, far simpler than analytic continuation and one that survives the journey more intact, concerns the index laws. You take the well understood concept that a times a times a... n times is a^n, and uncover the fact that a^m times a^n = a^(m+n). Then generalise the concept of power so you can consider things that "don't make sense" like a^(1/2) or a^(-3). These are not meaningful under the initial view that "power means repeated multiplication", but the extension and subsequent exploration lead to important and very meaningful results. Learning the index laws can be an exercise in rote memorisation, or it can be a wonderful journey of discovery, where seeming "nonsense" becomes clarified and empowering!
Numberphile demonstrate this side of maths, and should absolutely be congratulated.
Anonymous
"More important" than what? More important than truth, precision, clarity, correctness, understanding, etc.? Many Numberphile videos are fun and all that in addition to being essentially correct. However, they really blew it with the nonconvergent-series videos.
You might consider steering students to Martin Gardner's books based on his Scientific American column "Mathematical Games"; even though he wasn't a mathematician, he had lots of contacts in the mathematical community, and his writing was clear, entertaining, and essentially correct.
Anonymous
I have to disagree, and am quite bemused by the moral tone taken up by some of the detractors of this work. It's too easy to dismiss these videos as incorrect/untruthful etc. In context, they are a valid exploration of mathematical ideas, and thus important and valuable.
In the history of maths, this happened with irrational numbers, negative numbers, imaginary numbers. Formal manipulations that included "nonsense" ended up enriching mathematics. And in modern maths, look at p-adics where, for example. in the 5-adics, 5+5^2+5^3+... converges but 1/5 + 1/5^2+1/5^3+... does not. There's the Umbral Calculus where the formal basis is still only being constructed. Also, the extended complex plane where infinity is just a point like any other.
Now you can say they sneakily departed from real numbers, but the whole question naturally goes beyond the reals because it involves infinity. Infinity is not a real number, but more relevant, it is not just a "really big number". That it is qualitatively different is important to learn, and apparent from ideas like divergent and non-absolutely convergent series. As a 15 year old I was introduced to 1+2+4+8+...=-1 by a maths professor on an excursion, and it made a tremendous and positive impression on me and my fellow students. And I use similar things to both communicate my love of maths, and to encourage others to look at it differently and find their own sources of wonder.
And it is not so far removed from school maths. We teach that infinity - infinity is undefined arithmetically, but in terms of sets we often show that it can have many values (easiest example is remove all even numbers from 1,2,3,4,5... and you are left with an infinite set, compared to match up 1<->2, 2<->4, 3<->6 etc and show that none are left behind). Exposure to such conflicts is a great and fun way to learn about the limits and context of maths. And a major source of error is not learning the limits, applying things unthinkingly out of context, because too much exposure is only to "nice" examples. There is loads of education research on this. These paradoxical results force students to confront the limits, and thus can be used to enhance their mathematical thinking.
The authors of the article recognise the broader context (although were clearly not entirely happy with the presentation). The commenter above, Matt E, a maths teacher, seems to miss this broader context. Of course, approaching and crossing boundaries may well mean things need to be redefined, concepts generalised, but that's mathematics. Use it to generate interest, provide historical and real-world context, and thus enrich teaching.
Thinking about Grandi's series is like a first step on a journey. Enjoy it, and let students enjoy it too. Relate it to Thomson's Lamp. Bring mathematics to life!
p.s. Martin Gardner is great, certainly, but for a bit less puzzle orientation I recommend "The Heart of Mathematics: An Invitation to Effective Thinking", by Edward Burger and Michael Starbird.
Luca Gasparro
As the leading professor at the university of Cambridge with 10 PhDs within the world of maths, I have to quite frankly state your opinion is invalid. You forgot to differentiate the function zx : zy accordingly before putting it into partial differentials.
Kellen
I really just wish they had put some sort of disclaimer in their video about their math trickery. As a current math major who's done some work with infinite series, I was skeptical of their claim that (-1)^n converges to 1/2 and so just ended up being confused when they said that the sum of all natural numbers converging to -1/12 was consistent with modern physics. Now, a while after seeing the video I decided to do my own research and came upon this article which was very helpful in understanding what was actually going on. I suppose I have a different perspective on math than the average person, but I was much more satisfied with this, correct explanation, than their hand-wavy one.
Tomaž Podobnik
Kellen:
> I was skeptical of their claim that (-1)^n converges to 1/2
I don't think the authors of the video ever claim that the sum 1-1+1-1+... converges. The partial sum S_n
(the sum of the first n elements of the series) is either 0 for n even or 1 for n odd, which means that the
partial sums do not have a limit and so the infinite sum 1-1+1-1+... does not converge.
Jean-Marie Ntipouna
Z=1-1+1-1+....... has two possible results only : 0 or 1 depending on where you stop. So
you have Z=0 or
Z=1
_____
2Z=1 therefore you can write Z=1/2 (remember that we are working with infinity and have in mind Cesario sums)
Etc.....
Andrew Karsy
Think about it. At the start with the 1-1+1-1+.... Being wrong, is simply wrong. Because of the part where they say 1-1+1-1+1-....+1-1+1-1+1-1+.... is as wrong as putting decimals after a repeating number. Even if this is true, you are assuming that the sum ends with -1. in order to have the second sum start with +1 which is absurd because if the sum ends with -1 (which defeats the purpose anyway) then Z=0. And if Z=0 then 2Z=Z is true. Because 0+0=0 not to mention that it isn't even the original sum anymore.
J
I agree. I was staring at their addition of the two infinite series for a while trying to make sense of it. It doesn't make sense. It also doesn't address the fact that using the formula for an infinite geometric series (S = a / (1 - r)) with a = 1 and r = -1 doesn't work here.
Not impressed.
hk
i agree with you. if u are taking Z as 1-1+1-1+1..., you cannot assume that Z and Z is also 1-1+1-1+1..... Z could either end with a +1 or a - 1, thus, if it ends with a +1 Z and Z gives 1-1+1-1+1-1+1........1-1+1+1-1+1-1....... you would get a 1+1+1 in the section between the first Z and the second Z. which means Z+Z≠Z and so the infinite sequence 1-1+1-1+1-1+1-1+1.........is correct and equals to half.
Prince Verma
Try 1-Z= 1-(1-1+1-1......)
1-Z=1-1+1-1+1-1+1-1...
1-Z=Z
1=2Z
Z=1/2
Anonymous
you are absurd and shear wrong...the series stars with the positive 1...so it ends only in two possibilities it is either Z=0 (if the series have even nos of pairs ) or Z=1 (if the z has odd number pairs ending).. the Z=-1 is not a possibility at all
Raul Simon
Agreed.
Anonymous
You can't add two infinite series the way you did.
[ Z+Z ≠ 1-1+1-1+1-....+1-1+1-1+1-… .]
However,
Z+Z = 2-2+2-2+2-… ≈ 1,
which is consistent with, Z≈ 1/2.
berman
Not sure how to answer you. Non-convergent series are unpleasant and subtle things most 1st year mathematics text books will tell you the convergence properties of this sum. Instead let me just quote from Abel in 1828, "Divergent series are the invention of the devil and it is shamful to base on them any demonstration whatsoever". Hardy's excellent book on the subject explains the rights and wrongs; the good the bad and the ugly.
cincinnatus
But what if you did this:
Z = (1 - 1) + [1 - 1] + (1 - 1) + [1 - 1] + ...
The terms in round brackets sum to Z, as do the terms in square brackets. Thus, Z = Z + Z. In fact, Z = 3Z, 4Z and so on.
Angel
No, your argument is invalid, because you must realize that infinite summation is not commutative or associative, so putting brackets around certain numbers, and then re-ordering those numbers to change the order of the sum is not a valid operation.
Anonymous
This is what I've seen: there are ways that rearranging infinite series sums doesn't work. Most of the time if you get an answer like Z=1/0 then something's gone wrong.
Anonymous
It's cooooool.
Anonymous
The expression for S(-3) two lines below the two plates draw is wrong. It reads S(-3)= 1/2^3 + 1/3^3 + 1/4^3 +... and should be S(-3)=1/2^-3 + 1/3^-3 + 1/4^-3 +...
Thanks.
Marianne
Thanks for pointing that out! We've corrected it.
Anonymous
The Numberphile folks have a video that goes through basically the same area, talks about the sleight-of-hand in the shorter video, discusses analytic continuation and all that good stuff, and it's linked at the end of the short version. Well worth a watch: www.youtube.com/watch?v=E-d9mgo8FGk
berman
yes indeed, this is all good stuff and explains what lies behind it all.
Anonymous
Z = 1 - 1 + 1 - 1 + 1 - 1 ......
1 - Z = 1 -[ 1 - 1 + 1 - 1 + 1 - 1 ....... ] = 1 - 1 + 1 - 1 ..... = Z
1 - Z = Z
2Z = 1
Z = 1/2
berman
So, I will say it again..
Writing Z=.. and then assuming it is a well defined quantity is an assumption you cannot make.
The sum is nonconvergent. However you can very simply analytically continue the function that the sum represents beyond the radius of convergence but that is a continuation. The sum itself is not defined, it is not convergent. So if its nonconvergent don't write Z=..
It doesn't equal anything...
Anonymous
Ok, z= no longer means z is "equal to" when doing this. The one thing mathematicians do when making this tricky problem work, is change an equal sign to mean "associated with." When they do this, the result -1/12 actually becomes true. So all I have to say about this misleading article is this: Your maths about the 2z=z makes no sense at all. Much smarter people have worked this out and taken the answer -1/12 seriously, so I'm going to listen to them, not some random article.
Glen
While I understand the point you are trying to make, your assertion is flawed in a simple way: you assume that "converges to" and "equals" are the same thing, when discussing its value. Grandi's series doesn't converge; however, it can be considered equal to 1/2. This can be observed by seeing that its value is 1/2 using multiple different techniques, including continuation, Cesaro summation, and algebraic evaluation (as done by the person you were replying to).
Your argument in the article itself for why Z=1/2 doesn't make sense is flawed, as the series is clearly not absolutely convergent, and thus reordering an infinite number of terms can result in a different value, even where a series can converge (the classical example being the alternating harmonic series). To get "Z+Z=Z", you must rearrange an infinite number of terms, and thus the reasoning cannot work. On the other hand, the reasoning provided by the anonymous poster you replied to requires only a finite insertion, and thus "1-Z=Z" is reasonable.
Of course, the video (and thus Ramanujan) has the same flaw in their reasoning - they're reordering the infinite sums in a way that is inconsistent... but the video was just for lay people, and wasn't meant to be rigorous. More formal techniques agree with the result, and the fact that the same results can also be seen in physics indicates that "1+2+3+...=-1/12" is a meaningful statement, even if it shouldn't be interpreted as "the limit of the partial sums" in any sense - it shows that it isn't just a bit of mathematical sleight-of-hand.
Anonymous
statement is logically faulty ;
substitute : z=zero
result : one minus zero is zero !!!
facit : give me a buck (=1) for each such transaction !
Anonymous
Anonymous proves their own point by using nonsense themselves? huh?
a buck? might as well give you an imaginary goat instead.
Anonymous
Dude... pls... stop. do you know what solving an equation means?
Anonymous
Z is an unknown variable. The only value that fits there is 0.5.
Mousam
Z is not an unknown variable. It is used to identify the infinite series 1-1+1-1+1-1+1-........
so when he said 1 - z = z, he meant
1 - (1-1+1-1+1-1+1-1+...) = 1-1+1-1+1-1+.....
Abhinav
U cannot put z=anything
Basic linear eqn
Any variable can have only one value for a single eqn
Abhiram Cheruvu
I love maths
Táhmahnáh Tycró
I'm sorry, but why did you substitute Z with zero? Where the hell did you get that? I think you forgot that the equation is not a function, and you can't substitute it with a value of zero, since we don't know the value of Z yet. You can't contradict a statement and substitute it with a value since the person is still trying to find the value. Also, 1-1+1-1+1... is Grandi's series, search it, and its been proven that the sum IS negative one, as proven by the diverging averages of the partial sums to one-half
(1/1), (1+0)/2, (1+0+1)/3, (1+0+1+0)/4, ... (1+0+1+0+1+0+1+0+1+0+1+0+1+0+1)/15, and so on. As you can see, it slowly alternates between other numbers and 1/2, but the difference between the alternates diverges to zero as the number of partial sums increase, thus, the equation does diverge to one-half.
Anonymous
I struggle with the second line of this...
If Z = 1 - 1 + 1 - 1 + 1 - 1...
1 - Z = 1 - [1 - 1 + 1 - 1 + 1 - 1...]
This leads me to believe 1 - Z =/= Z.
The pattern of Z alternates addition and subtraction, while the addition of the 1 - doubles up on subtraction. If we assume the pattern continues and you stop at a given point, the two results do not match (perhaps someone smarter than I could prove).
After 3...
1 - [1 - 1 + 1] = 0
1 - 1 + 1 = 1
After 4...
1 - [1 - 1 + 1 - 1] = 1
1 - 1 + 1 - 1 = 0
After 5...
1 - [1 - 1 + 1 - 1 + 1] = 0
1 - 1 + 1 - 1 + 1 = 1
If you need a further example of what I am seeing, let's rewrite as
Z = 1 + (-1) + 1 + (-1) + 1...
1 - Z = 1 + (-1) + (-1) + 1 + (-1) + 1...
The alternating nature of the pattern is not the same, we have double (-1), so:
1 - Z =/= Z
This ruins the rest of that series of equations.
I feel like I am missing something, perhaps someone with more experience could explain.
Anonymous
I'm not sure what you mean by "doubles up on subtraction." it looks like a math error to me. The equation
1 - Z = 1 + (-1) + (-1) + 1 + (-1) + 1...
is wrong. The correct derivation is
Given: Z = 1 - 1 + 1 - 1 + ...
1 - Z = 1 - (1 - 1 + 1 - 1 + ...)
1 - Z = 1 - 1 + 1 - 1 + 1 - ...
1 - Z = Z
You got all of the previous (finite) examples right, but they are irrelevant. The equation 1-Z=Z works only for the INFINITE series.
Anonymous
Ok so I have read the article and watched the shorthand proof on numberphile. However don't the natural numbers have a closure property, meaning if you add any of the natural numbers together you must get a natural number? So how can it be that when we add all of them, we get -1/12, which does not belong to the natural numbers? I think my idea of adding all the natural numbers doesn't match with what is going on in the article, so if anyone could fill in the gaps that would be great.
berman
Very good, the naturals are closed under addition. And indeed the point of this article is that the sum of all naturals is not -1/12. Only the so called regularised sum where "an infinity" has been subtracted- that "infinity" is obviously not a natural.
Anonymous
Ok thanks for the response, sorta wanna get my head around this incase I tell people about it. I like how Numberphile made a separate video for the sequence S1 = 1/2, cheeky way to get more views. Where this all loses me is where the extended function gets its values from when you plug in values less than 1 (somewhere in the article it says less than -1, is this a mistake, what about -1
berman
yep it should be less than or equal to -1.
So exactly where does it get its value from? This is the technical bit about analytic continuation. There is a way, beyond the scope of this article to extend functions of complex numbers once you know the value of the function elsewhere. I understand why the numberphile people didn't want to bring that up because it is hard to explain nontechnically and indeed to give them credit where it is due, they have a discussion about it in an adjoining video and a written bit about it now too. So basically there is a bit of maths using function of complex numbers that allow you to assign a value to a function once you know its values elsewhere. The point of the artice was that this was too hidden for my taste which is why we still get posts like the one above where they want to still claim that the sum of all the integers is -1/12. it is not. Only a function that is related to that sum has that value. Where by related I mean that function has the same value as that sum when that sum is convergent.
Anonymous
The closure of the natural numbers under addition means that the sum of any two natural numbers is a natural numbers. We can apply this principle again and again (finitely many times) to see that the sum of any finite number of natural numbers is a natural number. This however says nothing of the sum of an infinite number of naturals, which we have in the case of an infinite series; in fact we see that this need not exist at all.
Similarly, whilst rational numbers are closed under addition also, the sequence S given in the article for pi/6 gives an example of a series of rational numbers converging to an irrational number (the rational numbers are also not closed in another sense, as a sequence of rational numbers can converge to an irrational number).
Anonymous
The limit of a series of rationals can be irrational. (Pi^2)/6 is an accumulation point in Q. It element of the epsilon neighborhood of the partial sums Sn for a lage n. Sn is still part of Q for all n.
Anonymous
Thanks very much for this post - I feel like this is the follow up that like Numberphile is missing!
I'm not quite sure what Numberphile were thinking... I'm all for promoting discussion and argument, but even I have "limits" (-: Seriously though, I hope that Numberphile come back with a follow up video at some stage explaining themselves!
Anonymous
Hi,
I believe you have made a mistake in doing Z + Z = 2Z = Z
for 2Z to equal Z you have to assume that one of the Z sums ends at -1 so that the other can conveniently start at 1. This is a misconception as these are infinite series that have no end.
The only conclusion you can draw from Z + Z is as follows
Z = 1 - 1 + 1 - 1 + 1 - .......
+
Z = 1 - 1 + 1 - 1 + 1 - .......
which is equal to 2 - 2 + 2 - 2 + 2 - .......
Christian Whittaker email me at cpwhittaker@hotmail.co.uk if you are unsure (or disagree) with this
take out a factor of 2 you get 2( 1 - 1 + 1 - 1 + 1 - .....) = 2Z in which case you are back where you started
So because 2Z is not infact Z, your theory is irrelevant
Anonymous
I am far from a mathematical genius. However, this discards the aforementioned issue and issue raised in your comment that it must conveniently end with -1. If the 'final' term to this sequence is +1 then 2Z=2-2+2-2+2...+1. Same goes for the second 'Z.' I can't garuntee this is correct and without passing secondary school it is outside my general knowledge. Correct me if I am wrong or have mistakenly supported your argument...
Cheers
Anonymous
I think you misunderstood. We aren't saying that the series could theoretically end in +1, we're saying it doesn't end. so it would be 2z=2-2+2-2... If you place a 1 at the end it would mean 1 of 2 things. The series would end with +1, which it can't, or after the infinite series, you get a +1, which would not make sense, but even if it did it would never get to it. (Since the series is infinite) So im not completely sure what you meant, but the math doesn't work out for a series. Also, the article got that point wrong, as already mentioned. Therefor, I am not inclined to agree with this article. That is like saying there is evidence of teleportation but you messed up 2+2 in there.
Thanks