Trying A New Hat

I am hoping that you can help me out with my problem. I am finishing my final year at university in June. Ideally I would like to pursue a career as a financial analyst.

However, I have not studied maths A-Level and my degree is not highly quantitative. I know it sounds hopeless but would anyone at Plus know how I can turn from maths average to rocket scientist in the three months over the summer?

Is there an intensive course that you would recommend?

"Progress 101"

You could try contacting the institutions listed in our UK Courses guide. Searching their sites may yield something.

In addition, The Mathematical Association (UK) may be able to advise you further.

Goggling at Googols

My six year old came home from school saying the last number is google plus. Do you know what that is all about? Thanks.

Trish Youngman

Googol and googolplex are both very large numbers, though both finite (therefore smaller than infinity, for example).

A googol is 10 to the power of 100, or 1 followed by 100 zeroes.

A googolplex is 10 to the power of a googol, or 1 followed by a googol zeroes.

Here's what Kasner and Newman had to say about them in 1940:

Words of wisdom are spoken by children at least as often as by scientists. The name 'googol' was invented by a child (Dr Kasner's nine-year-old nephew) who was asked to think up a name for a very big number, namely, 1 with a hundred zeros after it. He was very certain that this number was not infinite, and therefore equally certain that it had to have a name. At the same time that he suggested 'googol' he gave a name for a still larger number: 'Googolplex'. A googolplex is much larger than a googol, but is still finite, as the inventor of the name was quick to point out. It was first suggested that a googolplex should be 1, followed by writing zeros until you got tired. This is a description of what would happen if one actually tried to write a googolplex, but different people get tired at different times and it would never do to have Carnera a better mathematician than Dr Einstein, simply because he had more endurance. The googolplex then, is a specific finite number, with so many zeros after the 1 that the number of zeros is a googol. A googolplex is much bigger than a googol, much bigger even than a googol times a googol. A googol times a googol would be 1 with 200 zeros, whereas a googolplex is 1 with a googol of zeros. You will get some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down zeros every inch of the way.

Three cheers

I WISH TO SAY THAT MATHS ROCKS!!!

"sophkno"

Drop-in drawings

Do you know where I can get comprehensive symbols and standard drawings (square, triangle, parabola) suitable for Word or a decent desk top publisher? All I want is to be able to drop them into my work to save me the bother of drawing them everytime.

Dave Finch

Things to try...

1. Seach for web clip art.
2. Any drawing package will give you squares/triangles.
3. Any plotting package will give you parabolas. Search for one - try www.tucows.org for starters.

Save them in a Word compatible graphic format, and there you go!

Goldbach is back

As I keep hearing conflicting information, can you tell me whether Goldbach's Conjecture has been proven correct at the present time?

And if not, how would one go about validating a possible proof of such?

Tim Lawrence

Goldbach's Conjecture remains unproven, and in fact Faber & Faber have recently offered a million dollar prize to anyone who solves it in the next two years - see our Issue 11 news story, Gold for Goldbach.

Sadly, it's likely that any proof that emerges will be understandable only by the most highly trained mathematicians!

LOGO and Statistics

I am a BEd student studying teacher training and am studying maths as one of my specialist subjects. I am required to complete two investigations/reports at a standard of A-Level but I need a starting point!! Can you suggest any such investigations on the following topics or web sites that may be of use to me?:

• LOGO: This has to be fairly simple because i have only recently been introduced to this topic.
• Statistics: I did A level Stats and can cope with this quite well but need some topic or investigation to start from.

I hope to hear from you soon.

Tracey Robbins

For LOGO, a good starting point is LOGOland on the NRICH site.

For Statistics, you could try some of the following articles from Plus:

• Puzzle No. 6 - world cup medallions
• Are the polls right?
• What a coincidence!
• Mathematics, marriage and finding somewhere to eat
• Dynamic programming: an introduction

So who are you anyway?

Brilliant website - but I was wondering the other day about who founded it, why, who it's aimed at etc.

Perhaps this could be included on the site. Perhaps it already is although I have yet to find it.

Jonathan Finch

It's a good question, and we thought it deserved a good answer! Please take a look at our new All about (Pl)us page for more information.

Subscription to Plus?

I am a US secondary math teacher.

How do I subscribe to your publication, either on-line or regular?

Steve Conn

Plus is a free web-site with no subscription requirements. It publishes 3 times a year. Keep an eye on the site for upcoming publication dates! Back issues are always accessible, so the site is building up into a useful resource.

Our sister site NRICH has further material, and there you can register online and participate in teacherly chat etc. NRICH publishes on the first of every month.

Using Plus material on a school website

Can we use any or all of the puzzles found on your Plus website on our school website if we acknowledge the source? What about the pictures? Can we use those?

C. White

We can't give a blanket permission for all pictures and puzzles because some material is used with permission from elsewhere. However, feel free to ask about specific items you'd like to use, and we'll give you a yes or no.

If we give permission for items we'd like an acknowledgement which includes a link back to our home page. We would also like confirmation that the school web site is not being used for commercial purposes.

Summing the squares

I stumbled across your web site whilst trying to find an answer to the following problem.

Quite simply, how do I express a formula to represent the total of the sum of squared numbers to the 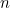$n$th integer? I know that 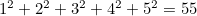$1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55$, but what is the formula that will get me to 55, given that (in this case) $n=5$?

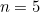Since the differences between successive totals are the squares of the integers, my guess is that quadratics must come into it somewhere. I'm sure the answer is staring me in the face, but I can't see it!

Any assistance would be gratefully appreciated.

Paul Stone

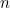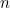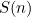There are quite a few ways to tackle this - you should find some in an A-Level maths text. One, as you spotted, is to use the method of differences to get the form of the answer - a quadratic in $n$ - then enter some known values for $n$ and $S(n)$ to derive the coefficients.

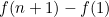Another method is to consider sums like this: \begin{displaymath} S(n) = \sum_1^n {f(k+1) - f(k)} \end{displaymath} Since most terms cancel, the result is $f(n+1) - f(1)$. Therefore all you have to do is think of some functions f that may help. You could try 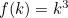$f(k)=k^3$ for starters.

Taking a STEP

I am currently a YR13 student at Lytchett Minster School, extremely interested in maths and studying hard for my exams in a few weeks. This includes Mathematical STEP papers II and III, and I have stumbled across this problem which has stumped both myself and my teachers. I would be grateful for any assistance on part (ii). [ Question 5, Maths STEP III, 28th June 1996 ]

5) Provide an expansion of 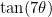$\tan(7\theta)$ in fractional form using de Moivre's Theorem. \par i) by considering 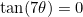$\tan(7\theta)=0$, obtain a cubic with integer coefficients whose roots are : 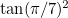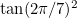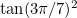$\tan(\pi/7)^2$, $\tan(2\pi/7)^2$, $\tan(3\pi/7)^2$, and deduce the value of $\tan(\pi/7)\tan(2\pi/7)\tan(3\pi/7)[X^3 - 21X^2 + 35X -7 = 0]$ \par ii) find, without using a calculator, the value of 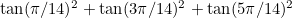$\tan(\pi/14)^2 + \tan(3\pi/14)^2 + \tan(5\pi/14)^2$

J. Daniel T. Jane

I presume you already have the answer to (i), namely the square root of 7. You found the cubic by considering 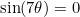$\sin(7\theta)=0$ (which is equivalent to 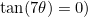$\tan(7\theta)=0)$, which has roots 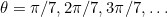$\theta=\pi/7,2\pi/7,3\pi/7,\ldots$ - this is important for the next part. \par For (ii), you need to use a similar approach to (i), but to find an equation with roots 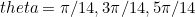$theta=\pi/14, 3\pi/14, 5\pi/14$ instead. Instead of 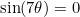$\sin(7\theta)=0$, think about 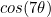$cos(7\theta)$ instead. You should be able to get a cubic 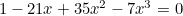$1-21x+35x^2-7x^3=0$, and use the formula for the sum of the roots. The answer is 5, as you probably already know from your calculator!