The world is upside down. Or at least, the version that our eyes send to our brain is. The clever trick that happens afterwards, putting everything back the right way up, is one of the first bits of neuroscience that most children learn. But the truly astonishing part — converting the blizzard of neural signals into a mental image of familiar objects — has puzzled researchers for years.
Until now, that is. Recent breakthroughs have begun to show how the process works — and how to exploit it. The discoveries have made it possible to control computer games by thought alone, or work out what kind of item someone is thinking about from their brain signals. And that's not all. Researchers at the University of California, Berkley were able to use brain scans to reconstruct what someone was looking at (a video of their results is shown on the right). In these experiments the scientists were literally able to see what people were thinking. A worrying thought, perhaps. But how did they do it?
Scanning the brain
The first step was to record the brain signals. To do this, the researchers used a technique called functional magnetic resonance imaging — fMRI for short. This is one of the newest ways to produce images of the brain. fMRI scanners, which capture the information needed to make these pictures, are feats of physics and mathematics in themselves (an overview is given here); they also allow us to see which parts of the brain are active at a particular point in time.
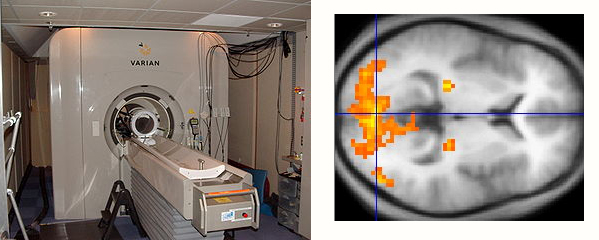
Left: fMRI scanner at the University of California. Right: Activity in the visual cortex.
This is possible because of the clues provided by blood flow in the brain. Like the rest of the body, when neurons are more active, they need more energy, and hence more blood. During an fMRI scan, these changes are measured by blood-oxygen-level dependence (BOLD).
If the person being scanned is watching a video, there will be BOLD signals in the visual cortex. But there is a problem: the changes in blood flow are much slower than the speed of the videos and are recorded as voxels — 3D pixels — rather than as a 2D image. It can therefore be difficult to take the images from the fMRI scanner and work out what they represent. To reconstruct the videos, the researchers needed to look at the BOLD signals in a different way.
Switching to a different space
How do you get from A to B? Most people will respond to that question in one of two ways: by drawing a map, or writing down a list of instructions. Both give the same basic information, but present it in a different form. In mathematical terms, the two approaches use different spaces: the map is in a familiar two-dimensional space; the list is in a space composed of all possible instructions.
The researchers working with the fMRI scanner also had two spaces to deal with: the two-dimensional film the person was seeing, and the BOLD signal, which represents change of energy over time in a 3D brain. But switching from one space to another is not always easy. The scanner told the researchers what BOLD signal they would get if they showed people a certain image (some of the scientists spent hours in the scanner watching video clips to get this data), but that didn't necessarily mean they could do the opposite. It's like drawing a graph. If you're given a function, you will often be able to plot it without much trouble. But given some random plot, it might be impossible to write down the original function.
So the researchers tried another approach. By comparing the signal from the fMRI scanner with BOLD signals from a large number of different clips, it would in theory be possible to work out what the video may have looked like. However, they would need a huge library of signals to get a good match – far bigger than they could obtain from experiments alone. To get around the problem, they created a computer filter that could convert video clips into BOLD signals without the need for an fMRI scanner. The filter had two stages. First, it took the video and transformed it from a moving 2D image – defined by an and
and 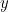 axis – to a space consisting of a set of neuron responses, each of which represents a feature such as spatial position, motion direction or speed. Then it converted this simulated neural activity into a BOLD signal.
axis – to a space consisting of a set of neuron responses, each of which represents a feature such as spatial position, motion direction or speed. Then it converted this simulated neural activity into a BOLD signal.
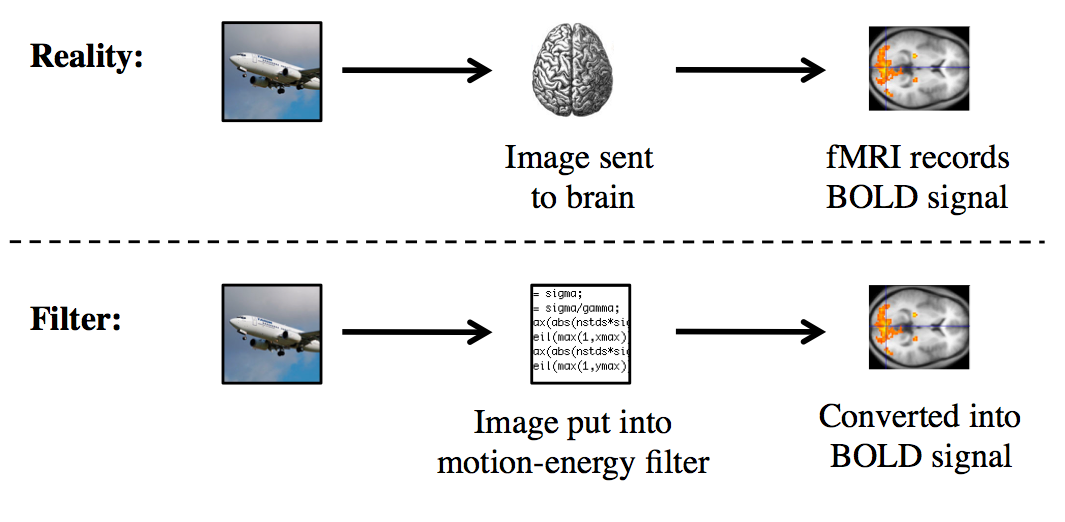
Filters can be used to simulate the BOLD signal for a given image.
Once they had tweaked the filter so that it could reproduce what they had already seen in experiments, it was possible to predict the BOLD signal for other videos without placing someone in an fMRI scanner. The researchers then put over 5,000 hours of YouTube clips through the filter and produced a library of BOLD signals for each one.
Next, by looking at the correlations between a real signal (from a person watching an unknown video in the fMRI scanner) and the predicted signals in the library, it was possible to assemble something that was likely to resemble the true picture. It didn't reproduce the video perfectly, but in many cases it gave a remarkably good approximation.
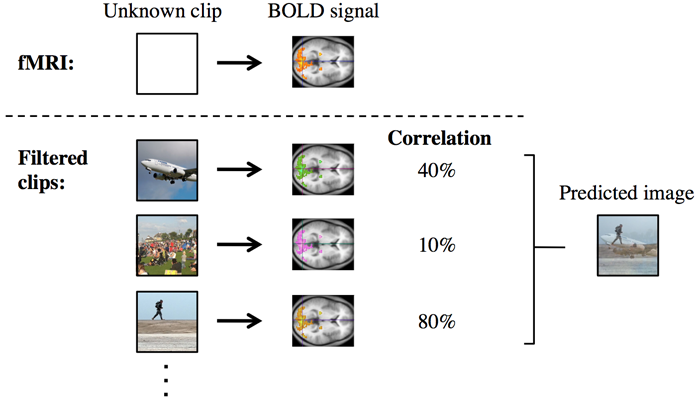
If the real BOLD signal is compared to the signal simulated for lots of other clips, the correlations can suggest what the image might be.
The comparison approach isn't just used in neuroscience. It has several other applications, including one found on digital cameras, Facebook and — as of last autumn — Android smart phones.
Facial recognition
What makes your face yours? Perhaps it's the shape: the position of your nose, the size of your eyes. In other words, we're looking at the problem in a simple 2D space again — the world of maps and videos.
There are other ways to tackle the question. One approach is to find similarities with other faces. You might look a bit like a number of well-known faces, for instance, a combination of a TV presenter, a tennis player and an MP. Of course, lots of other people will look a bit like that particular TV presenter too, but not many of them will also resemble the tennis player and the MP as well.
In fact, a surprisingly small number of comparisons are needed to narrow things down to a particular face. Facial recognition systems often use this approach. The faces that are used for the comparison are known as eigenfaces, which can be thought of as a set of "standard faces". Your face can be approximated by some combination of these eigenfaces, which are already stored in the system. It might be made up of the average face (the mean of all the eigenfaces), plus 45% from eigenface A, and 5% from eigenface B, and so on. (See here for another article on facial recognition using eigenfaces.)
A digital photograph is made up of thousands of pixels of information; the eigenface method can record your face using only a handful of values, each one referring to an eigenface used in the comparison.

The identity parade: nine different eigenfaces. (Image courtesy of Wikimedia Commons.)
Facial recognition has earned several mentions in the news this year. There was controversy when Facebook built it into their photo feature, and excitement when Google announced it could be used to unlock Android phones. After the London riots last August, law agencies used specialist software to track down the culprits, and they may use similar systems for the Olympics this summer.
The process of identifying a face using eigenfaces is similar to the fMRI correlation method. First, the 2D image of the unknown face is converted to a list of eigenface components, as follows. Say we have a 100x100 pixel photograph. The colour of each pixel is defined by a numerical value, so the image is given by a list of 10,000 numbers: we can think of this as a single point in a 10,000-dimensional space – call it  . The average face will be another point in this space. Now, if we start at the average face, moving to each particular eigenface takes us a certain distance away, in a certain direction. Some might take us near to the point
. The average face will be another point in this space. Now, if we start at the average face, moving to each particular eigenface takes us a certain distance away, in a certain direction. Some might take us near to the point  , others might not. However, if we have enough eigenfaces, there will be some combination of distances and directions that will take us from the average face to a point close to
, others might not. However, if we have enough eigenfaces, there will be some combination of distances and directions that will take us from the average face to a point close to  . The combination that takes us nearest forms our list of eigenface components.
. The combination that takes us nearest forms our list of eigenface components.
The list is then compared to other lists from a library of known faces, much like the researchers at Berkeley had a library of BOLD signals for known videos. This is the step that makes the facial recognition possible, as comparing lists of values is far quicker – and more accurate – than comparing photographs directly.
Ideally, it will be possible to find a list that matches the one for the unknown face. If not, a most likely identity is produced, in the same way that the neuroscientists obtained a most likely video clip.
Of course, we might not always be interested in recognition. We might just want to know whether the photograph contains a face — digital cameras often use this test to ensure that people are in focus. Suppose we want to check if a section of an image is a face. All we have to do is check that the set of eigenfaces for the image is similar to any of the lists in the database — we don't mind which list it matches, as we aren't trying to identify it. If, however, the set of eigenfaces is extremely different from any of the lists, then chances are that the image is not a face after all.
As well as eigenfaces, several other methods are used in facial recognition. Most either look at the shape of the face (geometric systems), or — as with eigenfaces — transform the image into a list of values and compare with a database (photometric systems). But both approaches need mathematics to power the recognition process.
Unravelling thoughts and faces
We have seen how important it can be to switch from one space to another. By taking a set of data and focusing on the key information – whether it's energy in a brain or what facial characteristics – it is far easier to make comparisons. Mathematicians have been doing it for centuries, and many of the techniques are essential to engineers and physicists.
The applications to biological problems are now becoming apparent too. Facial recognition systems, which are still less than twenty-five years old, are already finding their way into new technology. But it is the breakthroughs in computational neuroscience that may well be grabbing the headlines over the next few years.
The ability to scan a person's brain and determine what's on their mind will certainly raise some interesting questions, and a few ethical issues. However, it may also bring some huge benefits. It could improve the lives of the paralysed, change the way we approach everyday tasks and revolutionise how we look at memory and perception.
It might just turn our world upside down.
About the author

Adam Kucharski is a PhD student in applied mathematics at the University of Cambridge. His research covers the dynamics of infectious diseases, focusing on influenza in particular.