
Here’s a little game to play. Starting with any positive whole number 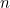 form a sequence in the following way:
form a sequence in the following way:
- If
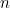 is even, divide it by
is even, divide it by 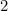 to give
to give 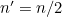 .
. - If
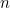 is odd, multiply it by
is odd, multiply it by 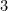 and add
and add  to give
to give 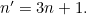
Then take 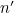 as the new starting number and repeat the process. For example,
as the new starting number and repeat the process. For example, 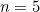 gives the sequence
gives the sequence
![\[ 5, 16, 8, 4, 2, 1, 4, 2, 1,... \]](/MI/f21203b21acf65df17a5658df78c0424/images/img-0003.png) |
and 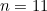 gives the sequence
gives the sequence
![\[ 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1,... . \]](/MI/f21203b21acf65df17a5658df78c0424/images/img-0005.png) |
Sequences formed in this way are sometimes called hailstone sequences because they go up and down just like a hailstone in a cloud before crashing to Earth. However, it seems that all hailstone sequences eventually end in the endless cycle
![\[ 4, 2, 1, 4, 2, 1. \]](/MI/f21203b21acf65df17a5658df78c0424/images/img-0006.png) |
The ones for 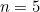 and
and 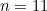 both do, though other values for may
both do, though other values for may 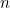 generate a very long sequence before the repeating cycle begins. For example, try starting with
generate a very long sequence before the repeating cycle begins. For example, try starting with 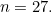 You can do this by hand, or use our hailstone calculator: enter any positive whole number and the hailstone sequence will be returned.
You can do this by hand, or use our hailstone calculator: enter any positive whole number and the hailstone sequence will be returned.
The question is whether every hailstone sequence eventually settles on the 4, 2, 1 cycle, no matter what starting value you use. Experiments certainly suggest that they all do. Computers have checked all starting values up to 5 x 260, a number that is 19 digits long, and found that the 4, 2, 1 cycle eventually appears. The trouble is that nobody has been able to prove that this is the case for all sequences. This open question is known as the Collatz conjecture after the mathematician Lothar Collatz, who first proposed it in 1937. It's amazing that such an easy recipe for forming sequences leads to a question even the best mathematicians haven't been able to answer yet.
Comments
code error
i tested you program and it failed for number 5
the sequence for 5 is 5, 16, 8, 4, 2, 1 definitly not 5, 16, 8, 4, 2, 1, 4, 2, 1,...
I think you missed the point
Try reading the article next time...
It seems from experiment that such a sequence will always eventually end in this repeating cycle 4, 2, 1, 4, 2, 1,...
No One Missed The Point
You are wrong.
If it reaches 1, it should not be continued.
He was correct.
Please do not give incorrect information to people.
yes
if it falls on an odd number you multiply by three and add one. so 5 would be 16 because 5 times three is 15 plus one is 16 so 5, 16, 8, 4, 2, 1,'' Please do not misinform people".
Correction.
The question doesn't state that you stop at one. It simply states that if its odd, you x 3 and +1, if its even you ÷ 2. Which would include the odd number... 1. So it would therefore repeat.
You are wrong.
In essence, the sequence will always cycle even after reaching 1, as stated by the rule.
The loop is the point of the conjecture
Terminating after reaching one would be mathematically inaccurate to the original conjecture. While the information after reaching one would be repeated, the 4, 2, 1 loop is the only reason that it terminates there. If it could continue past this loop then the conjecture wouldn't end at one.
Okay well...
The sequence technically does repeat 4, 2, 1 forever. We just chose to stop the sequence at 1.
code error
when you get to 1 (which is odd) the next result is 4, 2, 1....
Um not wrong
5 DEFINETLY DOES go 5,16,8,4,2,1,4,2,1,4,2,1,4,2,1,4,2,1.... The issue is that there are only 6, 4 or 3 numbers there that matter (depending on how you count)
You are either counting the 5,16,8 (so 3), the 5,16,8,4 (so 4, counting until you reach a 4) or 5,16,8,4,2,1 (so 6, counting until the repetition would start)
The sequence NEVER ENDS, but all (needs proof) eventually repeat 4,2,1,4,2,1 and so each sequence, even for the number 4 is infinitely long, we just don't care about after the repetition.
Perhaps you should re-read the article, and consider the original commentators work. The reason you are disagreeing seems as simple as how are you counting. You each are counting in a different way, yet seem to be saying the exact same thing.
The question isn't whether definitionally if 0 is or is not a natural number, you have to define whether it is and then do the math accordingly. I always asked my professors if they considered 0 in N or not for their classes. The guy you are saying is wrong, just defined his algorithm differently than you did. It isn't that you are right and he is wrong, or vice versa, it is that you both defined what you are looking for differently, but still validly.
Same holds for Fibonacci, does Fib start at 0 or at 1? If 0 is in N than the explicit formula for fibonacci is also different, yet they all are the same if you change the initial definitions to match.
0 is not in N, 0 is in the
0 is not in N, 0 is in the whole number set but not the natural number set.
But 1x3 is 3, plus 1 is 4 so
But 1x3 is 3, plus 1 is 4 so then you get to 4 again
Your right but wrong because
Your right but wrong because 1 times 3 plus 1 is 4, but it said that if its a even number divided by 2 so 4 divided by
2 is 2 divided by 2 is 1.
About your code error
It's a repeating sequence. The system is correct
Supposed Code Error reply
It definitely is because the rule of an odd is to multiply first by 3 so 5 x 3 is 15 and then add 1 which makes is 16 and when even it is divided by 2 so the result is 5, 16, 8, 4, 2, 1, 4, 2, 1...
Math
I hit 250 on the hailstorm sequence what do I do now?
It is not what you think
If you do this for a number like 17698739739579969 it will always reach one.
List of Lengths
My lengths are defined by stopping once a 4 is reached.
n=5 len=3
n=6 len=6
n=7 len=14
n=9 len=17
n=18 len=18
n=25 len=21
n=27 len=109
n=54 len=110
n=73 len=113
n=97 len=116
n=129 len=119
n=171 len=122
n=231 len=125
n=313 len=128
n=327 len=141
n=649 len=142
n=703 len=168
n=871 len=176
n=1161 len=179
n=2223 len=180
n=2463 len=206
n=2919 len=214
n=3711 len=235
n=6171 len=259
n=10971 len=265
n=13255 len=273
n=17647 len=276
n=23529 len=279
n=26623 len=305
n=34239 len=308
n=35655 len=321
n=52527 len=337
n=77031 len=348
n=106239 len=351
n=142587 len=372
n=156159 len=380
n=216367 len=383
n=230631 len=440
n=410011 len=446
n=511935 len=467
n=626331 len=506
n=837799 len=522
n=1117065 len=525
n=1501353 len=528
n=1723519 len=554
n=2298025 len=557
n=3064033 len=560
n=3542887 len=581
n=3732423 len=594
n=5649499 len=610
n=6649279 len=662
n=8400511 len=683
n=11200681 len=686
n=14934241 len=689
n=15733191 len=702
n=31466382 len=703
n=36791535 len=742
n=63728127 len=947
n=127456254 len=948
n=169941673 len=951
n=226588897 len=954
n=268549803 len=962
n=537099606 len=963
n=670617279 len=984
working on it....
Can you find out if the frequence of odd and even "len"s is 50% or not?
Yes you can know! And the
Yes you can know! And the answer is that there are always more even numbers in the sequence. If you assume the 50% hypothesis to be correct, it doesn't hold up. This is because if you have an odd number, the next term will always be even. This is because an odd number times an odd number (odd n times 3) is ALWAYS odd. That is true because if you multiply odd numbers, you can factor each number out, and 2 will not be a factor. This means that the resulting number cannot be divisible by 2 either, meaning it is odd. Anyways, if we assume that the 50% hypothesis is true, we know that an odd number will always be followed by an even one. So if the 50% hypothesis holds up, then every even number would have to precede an odd one. That doesn't hold up because if something is divisible by 4 for instance, you will be able to divide by two twice before you reach an odd number. Since the final cycle is always 4,2,1, and includes 2 even numbers and only one odd, there are always more even numbers than odd ones.
you're right
n=106239 len=351
n=142587 len=372
n=156159 len=380
n=216367 len=383
n=230631 len=440
n=410011 len=446
n=511935 len=467
n=626331 len=506
n=837799 len=522
n=1117065 len=525
n=1501353 len=528
n=1723519 len=554
n=2298025 len=557
n=3064033 len=560
n=3542887 len=581
n=3732423 len=594
n=5649499 len=610
n=6649279 len=662
n=8400511 len=683
n=11200681 len=686
n=14934241 len=689
n=15733191 len=702
n=31466382 len=703
n=36791535 len=742
n=63728127 len=947
n=127456254 len=948
n=169941673 len=951
n=226588897 len=954
n=268549803 len=962
n=537099606 len=963
n=670617279 len=984 is right
Something to think about...
It would be very interesting to know whether or not "stopping length" as a function of n exhibited any regularity, and if so, of what nature? If you plotted the "stopping length" of each sequence against the unique n that generated it, what would the graph look like?
Maybe someone with some programming ability can try this out...
There is an obvious pattern
Try 55, 115, 175, 235. All these have something in common
5
they all end in 5!
Good idea!
Challenge accepted.
the mother function of 3n+1
there i s function that when you let n=1 the collatz problem appears. but also, when N=-8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8...,infinity. as you guys can see, if we solve 3n +1, we will solve all of them. with the function is easy to find and loo of every roblem. why all numbers top at 1, is just because there are not positive numbers less than 0.
Answer
The number is divided by 2. If the resulting number is not a whole number, it is multiplied by 3 and 1 is added. Otherwise it is divided by 2 again.
Result for any number
Whatever number you enter, before the first 4 appears, the previous 6 numbers are always same (40,20,10,5,16,8). If it is an even number, it is preceded by 26,13 and if it is odd, then 80 and 160.
Exception
Not necessarily. Any power of 2 will just be devided by two over and over again and reach 16 without going through 5 first.
i noticed that too
i was reading these comments to see if anyone else had seen it but its not always 80 40 20 10 5 16 8 4 2 1 while i found that with alot of numbers there are some cases like 96 that come out as 24 12 6 3 10 5 16 8 4 2 1 always 10, 5, ect but before 10; 20 or 3 least form what ive seen :D
Simple version?
Hi.
If you change the steps to an much easier version:
if even divide by 2.
if odd add one.
Then you clearly always will end opp with 1. I`m not sure though how to write a proof of this, but you will always end up with the sequence (for n bigger than 2) 4,2,1,
Somehow related?
this is easy to prove
Consider that the n+2 iteration of the function is always less than the nth iteration.
the n+2 iteration is not
the n+2 iteration is not always less than the nth iteration, a mere look at the ending sequence shows that it can at least be equal:
\[ 4, 2, 1, 4, 2, 1. \]
in other sequences, the n+2 is actually bigger than the n.
That's because it has a
That's because it has a different ending cycle. Instead of having a 4,2,1,4,2,1,... cycle, it just has a 2,1,2,1,2,1,... so the original commenter is still correct
Goes into an infinite loop
Goes into an infinite loop and hangs when asked to evaluate 0.
Yes. The rules says 0' = 0.
Yes. The rules says 0' = 0. So, this needs a special case. And the conjecture should mention the special case! :)
My mistake. Zero is not a
My mistake. Zero is not a positive number, so is already excluded from the conjecture. The problem is with validation of the HTML form. It allows any number that can be typed, rounding and making it positive. Seems like it should reject anything but a sequence of digits that are not all zeros.
If there is a counterexample to Collatz
If there is a counterexample to the Collatz conjecture there is a minimum counterexample and it must be equivalent to 3 mod4.
Nice video on this problem
See the video "The Simplest Impossible Problem" https://www.youtube.com/watch?v=m4CjXk_b8zo
on the channel Tipping Point Math.
Possible advantage of a sieve method
I recently came across the Collatz conjecture and have spent some time investigating it. Although I haven’t found a proof of the conjecture I did wonder if a process similar the ‘sieve of Eratosthanes’ (used to isolate the prime numbers) might be used to isolate any integers that didn’t eventually home in on 1. Previous postings have established that we only need be concerned with odd numbers as even numbers divide down to 1 or an odd number so the sieving procedure is as follows:-
Step 1: List all the odd integers from 1 to infinity in column 1.
Step 2: Create a new column, column 2, and record the result of the function 3*n + 1 for each odd integer n in column 1 and reduce the calculated value to its smallest odd number. This obviously takes a long time to do as the column is infinitely long though these are the only calculations that have to be performed! Numbers such as 5, 21, 85 etc. have fallen through the sieve as they go straight to 1 in this step.
Step 3: Create a new column, column 3. Work down column 2 looking at each row in turn. Take the value on row n, column 2 and find the same number in column 1 then record the value found in column 2 at this row, in column 3 of row n. More numbers have now fallen through the sieve leaving fewer odd integers to deal with.
Step 4: Effectively repeat step 3 by forming a fourth column, and look up the values from column 3 in column 1 and record the values found in column 2 in column 3 of the initial row.
I tried to include a table to show how the above process works but, unfortunately, getting it to work in these comments seems to be beyond me at the moment, sorry.
I have tried this process in Excel, with odd integers up to 59995, and the first number which didn’t reach 1 was 703 but this was because it called for a number further down the list than 59995. Just less than 60% of the list went to 1 and this was achieved by column 17 which is much quicker and requires much less computation than the straightforward step by step method.
One thing I think we can conclude is that if there is a smallest number which forms a loop or which never reach 1, then this number must never reach a value in its sequence that is smaller than itself, as this value would, by definition, reduce to 1.
I have also derived formulae which will calculate all the numbers that would eventually lead to any given odd integer. I will post details of this later.
Sequence overlaps
This looks vulnerable to induction.
It looks very much like all sequences starting from an n_odd number contain the sequence for (n-1)_odd in the tail, and n = 3 ends in 4,2,1,4,2,1.
At some point a sequence starting from n_even will either reach an odd number part way through, and hence end in 4,2,1,4,2,1 by the above idea, or it will remain even and hence end in 4,2,1,4,2,1. E.g. n=8. = > 8, 4, 2, 1, 4, 2, 1,...
Sequence overlaps
Oops, I meant to write that it seems n_odd sequence contains (n-2)_odd subsequence.
New series
I worked out new series which always ends with sequence of 9, 4, 6 endlessly , i tried it on 25 numbers it works consistently. I want to take some help to prove sequence i have figured out will work for any number >3 .
New series
What was your piecewise hailstone function?
Old King Collatz: Number Theory: MyMathForum.com
To understand the "hailstone sequence", try reversing the process. All 3n+1 can be divided by 2 once, twice, or more. When the process is reversed, those which take three or more divisions serve as the basis of ever increasing "hailstone sequence" lengths terminating at the various demonstrable "odd entry gates".
Very interesting
Hmmm. Very interesting.
Hailstone-like sequence
Here is a sequence something like the "hailstone" one : starting from any number, if it is prime, multiply by two and add one, if composite, replace by its largest prime factor. This depends on there being a lot of primes of the form 2p+1 where P is prime. I don't know enough math to know how long those go on, but there are interesting sequencers for up to the 1000th prime.
Is x/2 even or odd, depending on the x given?
I am investigating on the hailstone problem for some fun. I found that g(x) = 3x + 1 is always going to be even if x is odd. How could I know wether f(x) = x/2 is even or odd, depending on the x?
Wasted effort
I did some calculations myself. I discovered after only a few minutes of boredom and intrigue that a massive amount of computing effort can save these simple rules
1. If at any given time an equivalent has appeared before of an equation that ended with a 1 the that equivalent and all in it are no longer vaild for the end result.
Example:6. Numbers not vaild would be 3,10,5,16,8,4,2,1. If one of these numbers has been reached then stop.
The end goal is not to find if every reaches 1.
Rather it is to find a repeated number. I bet you nearly anything that no equation that has been to reach has repeated the same number.