Bringing down the internet

How do you go about bringing down a terrorist network or containing a contagious disease? How many people need to know about a juicy bit of gossip in order for it to reach everyone? These kinds of questions have been on mathematicians' minds ever since the discovery of "scale free" networks in 1998, and now an international team of scientists have provided some answers.

A network is a collection of objects, called "nodes", which are connected to each other in some way. If, for example, the nodes are people, they can be connected by acquaintance, common criminal activity, or because one infects the other with a disease. The World Wide Web is a network, neurons in the brain form a network by the way they interact, we have networks in computer and transport systems, and businesses, such as banks, form networks through their dealings with each other. Even the Eurovision song contest, as Plus reported in the article United Kingdom - twelve points, forms a network sufficiently complex to be worthy of study.

The most important feature of a network is the way in which the "degrees" - the numbers of other nodes to which an individual node is connected - are distributed. Before 1998 it was thought that for most networks we come across this distribution is quite even - there is an average degree, probably a reasonably small number, and most other nodes' degree is somewhere close to this number.

Then, in 1998, the physicist Albert-Laszlo Barabasi and his colleagues modelled the internet, and to their surprise found that it behaves very differently from what they had expected: there are a few nodes, called "hubs", which have a much higher degree than the others. If you want to travel from one node in the network to another, you very likely have to pass through one of these hubs.

In fact, the probability 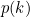$p(k)$ that a node is connected to 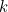$k$ other nodes is proportional to 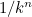$1/k^{n}$, where 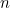$n$ in most cases is a number between 2 and 3. Barabasi christened these kinds of networks "scale-free".

Since then, many real-life networks have been found to behave like scale free ones, for example social networks, business networks and networks formed by the spread of a disease. If you think about it this makes sense: a new person coming along and joining a group of friends is more likely to do so via someone who is very sociable - the more friends you have the more new people you'll meet. And many other networks, such as disease and business ones, are based on contact between people and so behave similarly.

The big difference between scale free networks and those with evenly distributed degrees is that they behave very differently when they are under some kind of stress which causes individual nodes to drop out or fail. This could happen through an external attack on the network, like police arresting terrorists or doctors immunising people, or by internal strain, like congestion in a traffic or computer network. If you start eliminating nodes of a scale free network at random, then the network will remain pretty much unharmed for a long time, because the probability that you happen to take out one of the highly connected hubs is very low. You'd have to remove practically all nodes in order to break the network. By contrast, a network with evenly distributed degrees will fall apart quite quickly.

If, however, you know what you are doing, you can completely paralyse a scale free network by simply taking out a very small number of highly connected nodes - arresting three or four drug barons may be enough to put a town's drug trade out of action for some time.

But how many and which nodes do you need to eliminate? And what if your knowledge of the network is imperfect? The best connected terrorist is probably also the best protected, and it is hard to tell who is likely to give a disease to others. These questions were answered for theoretical models that mimic real-life networks by by Lazaros K. Gallos and Panos Argyrakis (Greece), Reuven Cohen and Shlomo Havlin (Israel), and Armin Bunde (Germany). In their paper "Stability and topology of scale free networks under attack and defence strategies", published in volume 94 of the Physical Review Letters, the scientists considered scale free networks in which the probability of a node being destroyed in an attack on the network depends on its degree. The better connected a terrorist you are, the better protected you are, and the smaller the probability that you will be eliminated. Conversely, if we are dealing with a social network, the better connected you are, the more visible you are, and the higher the probability that you will be attacked.

The results of the study show that you can bring down a network by eliminating surprisingly few of the nodes - even when you know little about it. If you have a reasonably good way of guessing which are the 1% highest connected nodes, then you can destroy the network by eliminating only 25% of the nodes. In other words, if you've got an inkling as to who are the most connected terrorists, or the persons most likely to spread the disease, then, if you go about it cleverly, arresting 25% of the terrorists, or immunising 25% of people, is enough to bring down the terrorists or contain the disease. If you know everything about the network, the percentage can decrease to 7%. Moreover, the scientists found that even if you do not manage to completely destroy the network, you can severely damage it by taking out a small number of nodes.

These results sound encouraging for people fighting diseases or terror. Unfortunately, the same goes for the bad guys, like those trying to bring down computer networks or the power grid. It all depends on who gets to the maths first.

Further Reading

• Read more about different aspects of networks in Plus articles Call routing in telephone networks and Agner Krarup Erlang.
• The Computerworld website has a nice introduction to scale free networks.