Nick Collins has a maths degree from Oxford and a Masters degree in music technology from York. Working in the arena of electronic music lets him combine his interest in maths with his love of music. Currently, he is in his third year researching towards a PhD in computer music at the University of Cambridge. He visited the Plus offices to tell us what he's up to.

"I am trying to build an artificial musician," Nick explains. "Some kind of autonomous unit that can sit on a concert stage and interact with human musicians. It would have to analyse acoustic music in real time, and then play back something that fits in with that music or compliments it." The ideal version of Nick's machine would be able to act as an improvisation partner: just like a Jazz musician, it would pick up on the other musicians' playing and respond with its own spontaneous composition.
But this is no easy feat. The human ear is a marvellous thing, finely tuned to picking up rhythm, beat, pitch and melody. To a computer, though, music is nothing but a tangled mass of information. The only way to make sense of it is to search it for patterns and periodicities — and this is an intensely mathematical problem.
Listening: how do we do it?
Even what seems a simple component of Nick's machine, a computer that can pick up a beat and "clap" along, is a huge challenge. "Getting a computer to pick up a framework for rhythm, beat tracking, is one of the fundamental problems," he explains. "And please don't imagine that it's straight-forward to build a device that can automatically transcribe music; extracting musical information from sound waves is a very special human ability."
When you pluck a guitar string or blow air into a saxophone, the string or air column vibrates, creating sound waves in the air. For musical sounds this vibration is an oscillation which repeats many times each second. The oscillation does not take the shape of one regular wave, rather it contains a complex mixture of many individual regular components, each with its own frequency of repetition. To analyse a complex oscillation you first need to break it down into these regular components.
For sounds typically used as musical sources, the frequencies of the various components tend to relate to each other in a simple linear fashion: there is a fundamental period within which one of the frequency components repeats. All the other frequencies repeat almost exactly at multiples of the fundamental. For example, you could have a fundamental repeating at 100 cycles per second (100 Hertz), and further components repeating at 200, 300, 400, etc cycles per second. We humans can perceive such a periodic waveform as pitch. The strength of different frequency components of the wave over time gives rise to our sense of loudness and timbre.

Machine listening: how maths substitutes brains
A computer, however, has none of the specially developed apparatus we use to analyse sound: not the tiny biological frequency analyser called the cochlear, which can separate sounds into their frequencies, nor the central auditory system's succession of neural centres that represent sounds. These can find pitch, localise sound sources and perform other clever tricks, many of whose secrets neuroscientists have yet to uncover.
But a computer does understand electrical impulses. When sound is recorded by a microphone, the varying sound signal is translated into varying electrical information. The computer takes a finite number of samples of this information and stores it as a string of numbers that approximate the pressure of the wave form. From here, we need to build our own frequency analysis. A particular family of functions is central to representing frequency mathematically: these are sinusoidal waves; functions of the form f(x) = ksin(cx+p). The number c determines the frequency, k determines the amplitude, and p tells you how far along the x-axis the wave has been shifted; it's called the phase.
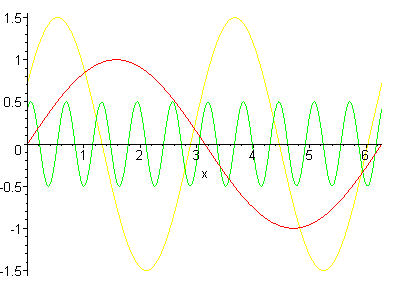
The graphs of three sine waves: the red function is f(x) = sin(x), the green
function is g(x) = 0.5sin(10x+1) and the yellow is h(x) = 1.5sin(2x+0.5).
Mathematicians use a tool called a Fourier transform to break the waveform from the sampled music down into a series of sinusoidal waves. Given a particular frequency, the transform performs a calculation that spits out a complex number which tells the computer whether the frequency is present in the sound and gives information about its amplitude and phase.
A huge challenge
What we've just described is called digital signal processing, and it's one of the techniques Nick uses to get a computer to track music. But don't get the impression that all this is straight-forward. Extracting further information from the output of a Fourier transform can become incredibly complicated. Nick says: "In general, computer music is not 'solved' because we don't know exactly how the human auditory system works. For example, if you have a complex sound scene, how do you isolate particular sound sources? At a party, how can you focus on a particular speaker? Humans can do this even when the background noise is more energetic than what they are homing in on.
"The current thinking is that there is no general beat tracker. Tracking a beat is related to stylistic constraints within the music, for example to the recognition of instruments, or streams. Basic musical processes are often interlinked, so that finding a rhythm can depend upon information about pitch, for example. In many types of music the important cues tend to be harmony and pitch. But those themselves can be influenced by metre, and metre in turn can be influenced pitch — it's a big challenge! With our wonderful brains we do things so automatically that it seems ridiculous that a computer can't do it. But machine listening is up there with the top modelling problems."
Given this difficulty, what can we reasonably expect from a machine at the present time? "You can get it to track a beat under certain circumstances, but it wouldn't be a universal tracker. Some systems have been built that can cope with pop music, the supposedly easy case. A lot of pop, in particular dance music, has been made to a certain recipe, it is quite rigid. It might be that certain components turn up quite a lot, like kick drums and snare drums. Sometimes you can find a beat in the music by looking for kicks and snares."
Composing with chaos
That deals with the listening side of things, what about composition? "I want the computer to generate something in response to the music which isn't just what it's been given," Nick says. "I want it to develop it in some way, or even to generate something completely new. This is where I use algorithmic composition." An algorithm is a recipe, a predetermined set of rules which generate a particular output. In algorithmic composition, this output is finely detailed music.

Algorithmic composition isn't a new thing. Guido d'Arezzo (991- after 1033) devised a method for converting Latin texts into melody lines by associating each syllable to a certain pitch. Another example of a musical algorithm is the round, of which the earliest traced is Sumer Is Icumen In (1260). In the round, singers are instructed to sing the same melody line, but starting at set delays with respect to each other. These delay instructions are so automatic that machines could follow them. The maths here isn't very deep; it's simply "wait x number of beats and then reproduce the same sounds as in the original".
But more complicated mathematical formulas can be used, once you've decided how you are going to turn sounds into numbers and vice versa. For example, start with a pair of numbers (x,y). You can associate the pair to a tone by letting x determine the frequency and y the panning of the tone, i.e. the relative loudness of the tone in left and right speaker.
Then take a mathematical formula that transforms x and y into another pair of numbers. for example (x, y) becomes (x2 - y2, 2xy). This gives you a new sound with frequency and panning determined by the first and second coordinates respectively. Applying the formula again to the new pair of numbers gives you a third sound, then a fourth, etc. You can get a whole sequence of sounds, simply by repeatedly applying, or iterating, this formula — maths creates a song! You can listen to a tune which arises from an algorithm like this, programmed by Nick, and look at the function underlying this algorithm. He used a programming language called SuperCollider, especially developed for audio. Click here if you would like to see the code.
The mathematicians amongst you have probably already spotted that there's endless fun to be had here: iterated functions, or systems of functions, give rise to fascinating phenomena like chaos, fractals and self-organisation, and this is a way of putting these phenomena into musical form.
But Nick's work is not just about entertaining mathematicians. One brainchild of Nick's is an algorithmic composition system called BBCut, the "BB" standing for "breakbeat". As the name suggests, the system cuts up a musical input and then rearranges it, effectively remixing the piece as it goes along. The underlying algorithms are based on permutations, mathematical rules for swapping and substituting objects. With BBCut you can do anything from rearranging sequences of church bells to remixing your favourite artist by feeding in his or her music and then rearranging it to your heart's delight. Click here for some examples generated by BBCut.
The human element

klipp av at Bridge in Osaka, Japan.
Maths with its many algorithms and functions is a great source for an algorithmic composer to dip into. "Virtually any piece of maths that has a discrete output can be transformed into music," says Nick. But the question of how to transform a set of numbers into sounds and the choice of algorithms is still down to the human.
These decisions are informed by the psychology behind our enjoyment of music and by knowledge of how the human auditory system works. After all, there's no use in producing sounds that are off the scale of human hearing, or sounds that might be covered up by other sounds.
How, then, do you go about deciding which algorithms to use for composition? "It's like any composition process in the sense that you try lots of things out, you experiment to find what you like," he says. "Or you might even deliberately seek out what you don't like, to push yourself to find new areas. A computer can get you to places you wouldn't get to just by sitting at a piano and tinkering around, because it allows transformations that aren't based on pitch or rhythms."
Are there particular functions that give rise to especially harmonious music? "Well, the very idea of what is harmonious might depend on culture anyway," says Nick, "but often the search through mathematics can be a fruitful adventure, a novel experimental composition.
"Composers now work on a different level. Rather than creating one fixed product at a time, a particular song for example, they create a whole new life form which they endow with certain attributes and characteristics." The new life form is the artificial musician: equipped with rules and algorithms that tell it how to react to other players' music and create its own, it sits on the stage waiting to play with people.

klipp av
Nick has already produced functional programs. In a concert last year he tried out three different systems, one interacting with a human drummer, one with a human guitarist and one with a human sitarist. In each case the system's task was slightly different, ranging from subverting the musician's play to supporting it.
Fun
Nick's work is not just part of his PhD project, it also gets to go out and play. Together with the Swedish visual artist Fredrik Olofsson, Nick forms the duo klipp av (Swedish for "cut up"). He explains: "We have a live audiovisual splicing unit. Say you are in a club dancing with a camera watching you. If you're dancing to the music that we are producing, then we already know the beat of that music, because it's generated by one of my algorithms. So if we have a camera on you, we can make you stutter in time with the music. As we generate the music, we use the camera frames in a way that fits with it." See how this works on a rubber duck.

"But then there's an even more hardcore thing I do in live performances. It's called live coding. It's a very, very underground scene that is only now gaining some press. Basically it's about attempting to program in front of a live audience. You are making a program that makes music, and in front of the audience you are changing the program, which in turn changes the music. It leads to a sort of live maths. It's like a rap battle but with programs. It's a very experimental thing and we are still figuring out the best ways of doing this."

klipp av
Nick uses SuperCollider in these coding battles. The audience watch the coding on projections of the computer screens and hear the music being generated in real time. Perhaps you do have to be a bit of an expert to enjoy these gigs? "People do have some problems with these kinds of performances. The main complaint usually is that it's not gestural, like an ordinary musicianship. But we've already discussed how computers make composers think on different levels. It's no longer about producing individual events, like one individual song. It's on a level of creating systems which create the events. So in that sense it's just different to traditional acoustic music."
Different indeed and not what most of us expect from a live gig. But who knows what the future will bring? Computers open up a world of possibilities for musicians and other artists. Not only does new technology allow them to do things that previously were simply impossible. Computers also open the door to the weird and wonderful world of maths with all its beautiful patterns that seem to lie at the core of nature. With all this at an artist's disposal, doing maths may become an ever more integral part of making music.
About the author
Marianne Freiberger is co-editor of Plus.