
Natural frequencies and music
Musical instruments are able to create sound because of a property which they share in common with most structures, that they can be made to vibrate at one of a set of frequencies with ease. At all other frequencies it is a struggle. The frequencies to which they naturally respond are called natural frequencies, and the corresponding shapes into which they deform during the vibration are called modes. It is usually the first, or lowest, natural frequency which is dominant.
If you give an object a knock you will hear a sound which occurs because it has been set vibrating at its natural frequency. This is related to the shape of the object and the material from which it is made. Hit a table with a knuckle and then tap a book; the softer material makes a sound of lower frequency (both sounds die away quickly because of the dampening property of wood and paper). Musical instruments take advantage of this phenomenon by using materials and shapes giving rise to pleasing sounds which can be sustained into a melody.

Figure 1: A musical ruler.
As a practical example consider a ruler or similarly shaped piece of material. Hold part on the edge of a table with the rest hanging free, press the free end and then let go. It oscillates back and forth creating a sound. The frequency can be raised or lowered by shortening or lengthening the freely hanging part - try it!

Figure 2: A musical bottle.
A second experiment to illustrate the way that musical instruments create sound, this time through the vibration of a mass of air, is to blow across the top of a bottle. It is fairly easy to excite the air inside to vibrate, and you can vary the frequency by adding water to change the volume of air.
The frequency of a vibration is the number of cycles per second and is measured in Hertz (Hz). In the picture below there are approximately 19 cycles in 0.04 seconds, so the frequency is about 475Hz. The note A, played by an orchestra, has frequency 440Hz.
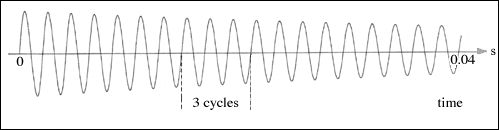
Figure 3: 475 Hz.
A 7cm overhang of a typical ruler will give a frequency of about 200Hz.
Mathematical modelling
The simplest mathematical model of these vibrations comes from a mass vibrating on a spring.
Newton's law says that force is mass times acceleration. After the initial exciting force has been taken away only the spring effects the vibration. The equation of motion becomes:
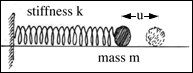
where u is the displacement of the mass from its equilibrium position and k is the stiffness of the spring.
This differential equation has two possible solutions:
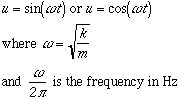
You can see from this that increasing the stiffness of the spring (larger k) will raise the frequency and increasing the mass will lower the frequency.
African Piano

Figure 4: An mbira
The instrument at left is an mbira or African piano. Instead of a thin piece of wood or plastic it has reeds made from flattened steel. These reeds are usually made from beaten out builders nails where skill is needed to obtain the shape giving the required tone.
The mbira is played throughout large parts of Africa; currently in Zimbabwe it is used in amplified form by some of the bands playing commercial Afro-rumba music in night clubs and on CDs. You can see the variety of reeds, each associated with a particular note. Traditionally these are plucked with the fingers in a cyclic, rhythmic pattern producing calming, slightly hypnotic melodies. In this form the instrument was used at religious ceremonies to create a suitable atmosphere.
The art of instrument making
Most instruments use one or other of the two forms of vibration discussed here: structure or air or a combination of both. Think of an instrument and you can probably see the forms being used although may-be in a fairly complex interaction.
For example, the sound from a violin is initially caused by the bow setting the strings vibrating (structural) but this is amplified by transferring the vibration to the wooden casing (again structural). However, the shape of the casing will affect the way the air inside vibrates, influencing the quality of the sound (air vibration).
The art of making musical instruments comes from creating shapes and enclosing volumes of air to exploit natural forms of vibration.
About the author
David Henwood is a Senior Lecturer of mathematics at the University of Zimbabwe.