December 2007
Finding the maximal efficiency
We want to calculate the maximum value of windmill efficiency 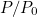 . Write
. Write 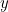 for
for 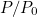 and
and  for
for 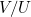 . We get
. We get
![\[ y = \frac{1}{2}(1-x^2)(1+x). \]](/MI/d616dd060096419d7e35f52d0abf6ae2/images/img-0005.png) |
![\[ dy/dx = \frac{1}{2}(1 - 2x - 3x^2). \]](/MI/d616dd060096419d7e35f52d0abf6ae2/images/img-0006.png) |
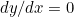 , in other words when
, in other words when ![\[ 3x^2 + 2x - 1 = 0. \]](/MI/d616dd060096419d7e35f52d0abf6ae2/images/img-0008.png) |
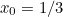 and
and 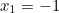 . Discounting the negative solution we get a maximal efficiency of
. Discounting the negative solution we get a maximal efficiency of ![\[ 1/2(1-x_0^2)(1+x_0) = 16/27. \]](/MI/d616dd060096419d7e35f52d0abf6ae2/images/img-0011.png) |
Read more about...