This issue's Pluschat topics
- Plus 100 — the best maths of the last century
- More maths grads
Plus 100 — The best maths of the last century

To celebrate the tenth anniversary of Plus, we would like to honour the generations of mathematicians whose flashes of genius or years of struggle have provided mathematics with its greatest advances, and us with an unlimited amount of fascinating things to write about. Last issue we concentrated on the last decade, but in this issue we expand our horizons to the last century. We've asked people to nominate what they think are the most important mathematical advances of the last hundred years, and below are some of our favourites. If you think that something is missing from this list, turn to last issue's Pluschat for the best maths in the last decade, and if you don't find it there either, drop us a line.
Here are our favourites from the last hundred years:
- Gödel's Incompleteness Theorem;
- The invention and development of the computer;
- The Four Colour Theorem;
- Advances in theoretical physics;
- The mathematical understanding of chaos.
You can find out more about the history of Plus in last issue's How time does PASS and this issue's Maths goes public. In the next issue of Plus we'll consider the best maths in the last 1000 years. Your suggestions are welcome!
Gödel's Incompleteness Theorem
In the early 1930s a young and troubled genius named Kurt Gödel proved a result that demolished the hopes and beliefs of many mathematicians. He showed that those fundamental building blocks of maths — the whole numbers — can never ever be encapsulated by a self-contained mathematical system. No matter how rigorously you define what you mean by "the whole numbers", or how thoroughly you stick to the rules of logic when you try and prove things about them, there will always be some statement concerning the whole numbers that, although you know it to be true, you cannot prove within your system. To prove it, you have to appeal to some higher authority outside of the system. What's worse, Gödel showed that you cannot even prove that the basic rules you based your system on — the axioms — do not contradict each other.
It's hard to see how maths can be used to prove the limitations of maths, but you can get a glimpse of the kind of brain-twisting involved by looking at language examples like the sentence
If you could prove this statement to be true, then it would be false! It is true only if it is unprovable, and unprovable only if it is true. Gödel devised an ingenious way of translating sentences like these into numbers and hence derived his result.

Kurt Gödel. Photograph by Alfred Eisenstaedt, taken from the Gödel Papers courtesy of Princeton University and the Institute for Advanced Study.
The Incompleteness Theorem obviously has huge philosophical implications. It frustrated all those who, along with David Hilbert, had hoped that all of mathematics could one day be phrased in one consistent formal axiomatic system; a mathematical theory of everything. Gödel himself did not believe that his results showed that the axiomatic method was inadequate, but simply that the derivation of theorems cannot be completely mechanised. He believed they justified the role of intuition in mathematical research.
The theorem also has some very real implications in computer science. This is not surprising, since computers are forced to use logical rules mechanically without recourse to intuition or a birds-eye view that allows them to see the systems they are using from the outside. One of the results that derive from Gödel's ideas is the demonstration that no program that does not alter a computer's operating system can detect all programs that do. In other words, no program can find all the viruses on your computer, unless it interferes with and alters the operating system.
Gödel's Incompleteness Theorem has been misunderstood, misquoted and misinterpreted in many highly amusing and extremely annoying ways. It's been used to prove, among other things, that god exists, that maths is useless and that all scientists are evil. Type it into your search engine, and you'll find tens of thousands of crack-pot interpretations. But if you'd like a reliable and authoritative account of the theorem and its consequences, then read Plus articles Gödel and the limits of logic, Omega and why maths has no TOEs and The origins of proof III.
The invention and development of the computer
We don't need to explain how important the computer has become to modern society. If all computers were to disappear tomorrow, not only would Plus cease to exist, but the whole developed world as we know it would collapse. It's amazing to think that it's only taken a few decades to turn computers from huge, room-filling monsters into the tiny, ubiquitous and all-powerful machines they are now.

A 19th century loom operating on punch cards. Image from Wikipedia, reproduced under the terms of CeCILL,
But what is a computer? Stretching the definition a little, computers have existed at least since 2400 BC, introduced by the Babylonians in the shape of the abacus. Over the millennia many great minds, including Leonardo da Vinci, Gottfried von Leibniz (one of the inventors of calculus) and Blaise Pascal (of Pascal's triangle), have utilised cog wheels, pulleys, glass tubes and clockwork mechanisms to build ingenious calculating devices. The fist computer-like machine to be mass produced was designed by the weaver Joseph Jacquard, and took the shape of an automated loom operating on punch cards, a method that will still be familiar to our older readers.
To mathematicians, however, a computer is something far more abstract. It's a universal machine that, based on simple logical commands like "if this is true then do that", can execute any logically coherent string of instructions, whether they refer to operating a loom or booking your summer holiday. The idea that all kinds of thought processes, not just arithmetic calculations, might be automated and relegated to machines already occurred to Leinbniz in the 17th century, and he refined the binary number system now so indispensable to computers. In the nineteenth century, the mathematician George Boole laid the foundations of computer programming by reducing logic to an algebraic system that is capable of operating on the two humble symbols 0 and 1. At around the same time, Charles Babbage, inspired by Jacquard's loom, envisioned his own version of a universal machine, the analytical engine. Although he never built the machine, his theoretical considerations, annotated and extended by Ada Lovelace, proved to be logically sound.
It wasn't until the 1930s, though, that the theory behind computers was clinched, first and foremost by the British mathematician Alan Turing. Turing showed that it is indeed possible to build universal computing machines that can do anything that any other computing machine — like for example Jacquard's loom — could possibly do. He also examined the limits of such a machine, entering the mathematical territory that was also explored by Gödel. In fact, Gödel's Incompleteness Theorem (see above) is sometimes called the fundamental result of theoretical computer science.

The Colossus Mark II computer was used to break German ciphers during World War II.
While the theoretical issues were being explored by mathematicians, others started building functioning machines. The world's first computer company was founded by Konrad Zuse in Germany in 1940, and in the same year produced the first programmable and fully automatic machine, the Z3. Like other machines it operated on electrical relays, or switches, whose on/off positions could implement binary logic and binary calculations. The first totally electronic digital computer, the ENIAC, was completed in 1946 at the Ballistic Research Laboratory in the USA. It weighed 30 tonnes, operated on the decimal system and had to be rewired for different programs.
In 1945 the legendary mathematician John von Neumann produced a theoretical design of a computer implementing the universal Turing machine. The first computer to be built and operated according to this design was the Manchester Mark I, produced in England in 1948. Most of today's computers are still based on the von Neumann Architecture. Computer design started to race ahead with well-known organisations like IBM, MIT and Bell Laboratories all contributing their bit.
Computers at this time were still huge, using vacuum tubes as mechanical relays. It was the invention of the transistor by John Bardeen, Walter Brattain and William Shockley in the late 1940s that opened the path for smaller and cheaper machines. The famed computer chip was invented independently by Jack Kilby, of Texas Instruments and Robert Noyce, who went on to found Intel, about ten years later. The first Intel microprocessor followed in the 1970s.

Getting smaller and smaller.
The 1960s and 70s saw the development and perfection of programming languages including BASIC and C, and of operating systems such as UNIX. Portable discs and the mouse appeared on the scene, and the idea of windows was first conceived. The word "computer" finally became compatible with the word "personal" with the introduction of graphical user interfaces in the early 1980s, exploited by both Microsoft and Apple Macintosh, and launching their battle over market dominance.
Since then, ever smaller and faster computers are being produced for home and commercial use, while mathematicians push the boundaries of artificial intelligence, resulting in ever more humanoid robots. The computer surge shows no sign of slowing and few would risk their reputation on predicting what will come next. As John von Neumann put it in the 1940s:
To find out more about computers and their history, read Plus articles Why was the computer invented when it was?, Ada Lovelace - visions of today, What computers can't do, and A bright idea. You can get an overview of the history of computers with the Wikipedia Timeline.
The Four Colour Theorem
Map makers have known for centuries that you never need more than four colours to colour a map so that no two adjacent regions have the same colour. In 1852 this problem came to the attention of mathematicians who ventured to try and prove what became known as the Four Colour Theorem. But, despite the theorem's apparent simplicity, this turned out to be fiendishly difficult. A first attempt by the English mathematician Alfred Kempe, published in 1879 in both Nature and the American Journal of Mathematics, was found to contain a flaw eleven years later.
Four is all you need.
The theorem remained unsolved for another century, when Kenneth Appel and Wolfgang Haken finally managed to prove it for a second time in 1976. Their approach, based on that of Kempe, would delight any mathematician in its straight-forward clarity. Appel and Haken assumed that there was in fact a map which needed five colours, and proceeded to show that this lead to a contradiction. If there are several five-colour maps, then choose one with the smallest number of countries: this is known as the minimal criminal for obvious reasons. Appel and Haken proved that this map must contain one of a number of possible configurations. Each of these can be reduced into a smaller configuration which also needs five colours. This is a contradiction because we assumed that we already started with the smallest five-colour map.
But instead of settling a long-standing problem, the proof opened up a whole new can of worms. Appel and Haken had to consider every single one of 1,936 configurations, and this could only be done on a computer. The number of computer calculations was so vast that no human being could in their lifetime ever read the entire proof to check that it is correct. This posed a huge philosophical conundrum: can you trust a machine to do maths? The mathematical community split into two camps: those who were prepared to accept the computer proofs and those that demanded a simpler version that can be checked by humans. A shorter proof of the Four Colour Theorem was in fact presented in 1996 by Neil Robertson, Daniel Sanders, Paul Seymour and Robin Thomas, but it still needed a computer, so the problem remained.
The issues around computer proofs do not just apply to the Four Colour Theorem. Other results, for example Kepler's Conjecture were also proved by computers, and with computers becoming ever more powerful the problem is likely to become even more pressing. In 2004 the venerable journal Annals of Mathematics, pressed by the presentation of the proof of Kepler's Conjecture, was forced to make a decision on its policy towards computer proofs. It decided that these proofs were essentially uncheckable and should be treated like lab experiments in the sciences: as long as they adhere to certain standards and satisfy consistency checks, they should be accepted by referees. Annals will only publish theoretical parts of proofs, leaving the computer sections to more specialised journals.
While mathematicians and computer scientists are busy developing fail-safe proof-checking mechanisms, mathematicians are still encouraged to come up with short proofs that can be checked by humans. In that sense, the Four Colour Theorem is still open.
You can read more about the Four Colour Theorem in the Plus article The origins of proof IV and about computer proofs in Welcome to the maths lab.
Advances in theoretical physics
The twentieth century brought advances in theoretical physics that were no less than revolutionary. The new theories rapidly diverged from our intuitive understanding of the world around us, and mathematics became the only language that could formulate them.
A complete account of all the theoretical physics that happened in the twentieth century would fill volumes, but we have just about enough space to skim over some of the most fundamental developments. The key words are relativity, quantum mechanics, quantum field theory and quantum gravity. The first of these four, relativity, was formulated in the years between 1905 and 1915 by a young and self-taught patent officer by the name of Albert Einstein.

Albert Einstein.
The idea that "things are relative" was not a new one. In the sixteenth century Galileo Galilei had illustrated the idea with the example of a moving ship: if you're below deck and the ship is moving smoothly and at constant speed, you can't tell whether you're moving or not. Any physical experiment you might perform, dropping a ball to the floor or throwing it up in the air, will give you exactly the same results as if you were on land. Motion is relative to the observer.
Isaac Newton later picked up on this idea by postulating that the motion of an object must be measured relative to an intertial frame, a frame of reference within which the object moves at constant speed and along a straight line. Newton showed mathematically that his laws of physics hold in all inertial frames (any two of which move in a fixed direction and with constant speed with respect to each other) and also postulated that there is an absolute notion of time.
The run-up to Einstein's special theory of relativity began in the ninetheenth century, when the physicist James Maxwell found that light was just another type of electromagnetic wave, and suggested the existence of a single all-prevailing ether, as the medium through which light waves propagate. Although proof for the existence of the ether failed to materialise in experiments, it was one of the strongest supporters of the ether theory, Hendrik Lorentz, who wrote down much of the mathematics of special relativity. Other scientists, including the mathematician Henri Poincaré, gradually moved away from the ether model, and in 1905 Einstein ingeniously reformulated Lorentz's mathematics into a new theory which did not assume its existence.
Einstein's special theory of relativity postulates that the speed of light is absolute and looks the same to all observers, while other notions like distance and time are relative. It gives rise to the famous equation e = mc2, which identifies mass with energy. The theory only applies to inertial frames of reference — hence the adjective "special" — and does not take account of gravity. Einstein understood that the effects of gravity could be described by a curved space-time and subsequently formulated these ideas in his general theory of relativity.
Einstein firmly believed in a static universe. His work on the general theory of relativity showed, however, that gravity would cause the universe to contract, and so he modified his equations by introducing a quantity known as the cosmological constant. When in 1929 Edwin Hubble's observations showed that the universe was in fact expanding, Einstein abandoned the cosmological constant as his "biggest blunder". Hubble's discovery eventually led to the Big Bang theory of the origin of the universe. The cosmological constant, incidentally, has recently received renewed attention from physicists.

Werner Heisenberg
Einstein also had a hand in the formulation of quantum mechanics. At the end of the nineteenth century many physicists thought that all natural phenomena, whether on Earth or in the heavens, could be described by the classical laws of physics going back to Newton. Physics could have been regarded as "all done", had it not been for a few experiments that defied any explanation in classical terms. In the first few years of the new century physicists including Max Planck, Niels Bohr and Albert Einstein realised that a mathematical explanations for the observed phenomena could be found if they substituted quantities that were previously thought to be continuous — the energy states of an atom at rest, or the energy of electromagnetic radiation — by tiny packages dubbed quanta.
In 1924 the French physicist Louis de Broglie built on this work and postulated that the world at a minuscule level is not made up of point particles and continuous waves, but of some strange hybrid between the two, a notion that became known as wave-particle duality. A new mathematical framework was needed to describe the emerging quantum theory. In 1925 the German physicists Werner Heisenberg and Max Born, and the Austrian physicist Erwin Schrödinger came up with two mathematical theories that were later shown to be equivalent. A famous consequence of wave-particle duality is the uncertainty principle, which states that you can never ever measure both momentum and position of a moving particle with the same high degree of accuracy. It was formulated by Heisenberg in 1927.
Quantum mechanics is in many ways extremely counter-intuitive. It suggests that the physical laws governing the world at a sub-atomic level are essentially probabilistic, postulates that the observer influences the experiment (Schrödinger's cat is famously both dead and alive at the same time, as long as you're not looking), and states that two particles can interact over long distances by the seemingly magical process of quantum entanglement. Nevertheless, it predicts physical processes at the sub-atomic level with amazing accuracy, and has become an accepted part of physics.
Stephen Hawking
The theories of relativity and quantum mechanics spawned the other major developments in twentieth century theoretical physics. The attempt to reconcile quantum mechanics with the special theory of relativity led to quantum field theory. First formulated by the physicist Paul Dirac in the 1920s, it achieved its modern form in the 1940s, with famous names including Richard Feynman and Freeman Dyson contributing to its development. Quantum field theory provided the theoretical basis for modern particle physics, giving rise in the 1970s to the standard model of particle physics. The model describes three of the four fundamental forces that determine the interaction of the fundamental particles, and so far has predicted experimental results with remarkable accuracy.
The force that is unaccounted for by the standard model is gravity, one of the main players in Einstein's general theory of relativity. Many attempts to reconcile general relativity with quantum mechanics have been made, but despite the efforts of eminent physicists including Stephen Hawking, there is no consensus as to which, if any, are correct. String theory is one of the main contenders for a theory of quantum gravity, but despite its mathematical beauty it remains purely theoretical and so far could not be tested against reality. A theory of quantum gravity would provide a physical theory of everything, and is currently the holy grail of theoretical physics.
You can read more about twentieth century physics in the following Plus articles:
- The physics of elementary particles;
- What's so special about special relativity;
- Quantum uncertainty;
- Light's identity crisis;
- Tying it all up;
- Quantum geometry.
The mathematical understanding of chaos
The word chaos generally stands for a complete absence of order and total randomness. The mathematical meaning of chaos differs from this in a way that at first sight seems extremely worrying: that unpredictability can arise from deterministic systems that are controlled by a set of clear-cut equations. This does mean that the world is not as orderly as many scientists, from the ancient Greeks to Newton, had hoped, but it also provides us with tools to tame the apparent unpredictability of many physical processes.
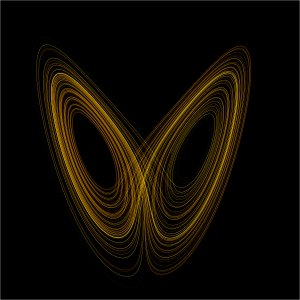
The Lorenz attractor. Image from Wikipedia, reproduced under the Gnu free documentaion license.
Many accounts of chaos theory trace its beginning to an event that occurred in the early 1960s. The American mathematician and meteorologist Edward Lorenz was running computer simulations of basic weather patterns. The simulations were governed by a set of differential equations, and each simulation had to be started off by a set of initial values. One day Lorenz ran the same simulation twice and to his surprise found that the two rounds resulted in completely different weather predictions. He soon found out why: the initial values of the second round had been rounded off by a seemingly insignificant amount. The tiny difference of starting values caused the equations to spit out a completely different set of answers.
What Lorenz had stumbled across became known as the butterfly effect: the tiny air currents caused by a butterfly's wing can amplify to eventually cause a hurricane half-way around the planet. To mathematicians this effect is known as sensitive dependence on initial conditions and it is one of the hallmarks of mathematical chaos. It means that even though your equations can predict the long-term behaviour of your system in theory, in practice they will never be able to do so, since an infinite degree of accuracy would be required to differentiate between initial values that lead to a completely different outcomes.
Lorenz wasn't the first to come across this phenomenon — it had been observed in physical and mathematical systems at least since the beginning of the twentieth century, and some of the maths that lies at the heart of modern chaos theory had been formulated then. But the millions of calculations needed to observe chaotic effects only became possible with the emergence of the computer, and so chaos theory only seriously took off in the second half of the twentieth century.
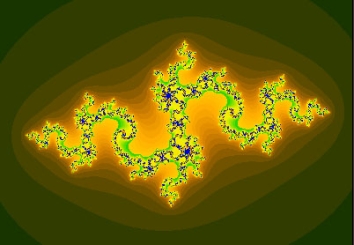
A Julia set, one of the beautiful fractals arising from chaos theory.
Since then mathematicians have given a precise definition of mathematical chaos, with sensitive dependence on initial conditions providing a key concept. They have detected chaos in a wide range of systems modelling physical processes. The humble quadratic equation, used to model population dynamics, has proved to provide chaos in abundance and has served as a guinea pig in mathematicans' attempts to understand this behaviour. They have explored the patterns emerging from chaos and those that give rise to it, and tried to predict its unpredictability. Their insights have impacted on a huge range of areas, from finance to neurology.
But no account of chaos theory would be complete without a mention of the beautiful pictures that arise from it. In many cases a dynamical system can be visualised geometrically, for example as the plane or as three-dimensional space. Once you have such a visual model, you can pin-point the regions where chaos arises. Lorenz was one of the first to do this and he came up with the beautifully intricate shape of the Lorenz attractor, which fittingly resembles a butterfly. In the 70s Benoit Mandelbrot created the first images resulting from systems governed by quadratic equations. With the increased availability of computing power, amazing fractal shapes appeared. Their beauty and intricacy rivals those of nature itself and mathematicians knew that they were onto something good. The geometry of chaos, as well as many of its other aspects, is still not completely understood.
You can find out more about the mathematics of chaos in the following Plus articles:
- Chaos in number land;
- Finding order in chaos;
- Chaos on the brain;
- Extracting beauty from chaos;
- Unveiling the Mandelbrot set.;
- A fat chance of chaos?.
Thank you to Tom Körner and John Webb for their suggestions
More maths grads
Three years after the Smith report on post-14 mathematics education, the government has pledged £3.3 million to widen participation in mathematics and increase the number of mathematics students at university. Recipient of the money is the aptly-titled More maths grads programme (MMG), designed by a consortium of mathematical organisations and launched in April this year.

We need more of these.
In the three years of its duration, the programme will focus on three target regions; East London, the West Midlands, and Yorkshire and Humberside. Each region will see a university — Queen Mary in London, the University of Coventry in the West Midlands, and the University of Leeds in Yorkshire — collaborating with seven specially selected partner schools, regional and national employers, as well as careers organisations. A fourth higher education institution, Sheffield Hallam University, will assess if and how mathematics degree courses should be modified to optimally prepare their students for working life.
The programme addresses some burning issues in maths: the lack of students' awareness of the applicability of maths and wide range of career options using maths eucation; the need to support teachers' professional development and add to their enjoyment of teaching maths; the lack of interaction between schools and universities; and the fact that women, ethnic minorities, adult learners and those from lower socio-economic groups are still under-represented in maths education and the mathematical professions.
The measures proposed are straight-forward. Get employers to visit schools and school students and teachers to visit universities, get university students to become "maths ambassadors" in schools, inform careers advisers, organise careers fares, organise enrichment events for school students as well as teachers, and make sure that teachers are supported by academic mathematicians. New resources informing about career options with maths will be created and disseminated through the Maths careers website. While no new teaching or teachers' professional development resources will be created, the jungle of existing ones will be catalogued and made available to teachers through the websites of the National Centre for Excellence in the Teaching of Mathematics and the MMG itself. Dissemination through these websites will ensure that the programme has an impact beyond it's three target regions, but there is also talk of extending the programme nationally after it's three-year pilot phase.
The government's commitment to maths education is commendable and the programme necessary. Although the number of students taking maths at university has increased recently, it is still nowhere near the level of 1986. With its focus on careers and the transition between school and university, the MMG programme addresses some of the weakest links in maths education. The simple and practical nature of the proposed measures gives them a real chance of succeeding.
But even with a clear strategy and a large chunk of money the MMG is not faced with an easy task. Three years is an awfully short time to make a real difference. The MMG's measures will have to take effect pretty much immediately, if they are really going to impact on student numbers. They also have to be sustainable; if they are not, any benefits will vanish in a puff of smoke at the end of the project.
Key to the MMG programme's success will be its skill in integrating existing projects and persuading all interested parties to come on board. School-targeted initiatives abound — the engineering, chemistry and physics sectors have all recently launched their own equivalent of the MMG — often adding to the workload of teachers already stretched to breaking-point. Wider initiatives already go a long way to delivering the MMG's declared goals, not least Plus magazine and its umbrella organisation, the Millennium Mathematics Project. Duplication of effort would delay the process unnecessarily and be a waste of taxpayers' money.
The MMG already has the commitment of four national employers, three of which are active in the defence sector. More regional employers will have to be found and the bias towards defence re-dressed, and that's no easy feat. Although employers frequently complain about the lack of maths skills in their workforce, they are often reluctant to give up time and effort to address the problem. (So if you work for a company that employs mathematicians and is active in one of the three regions, why not get in touch with the MMG?) Academics, too need to come on board. Often mistrustful of outside attempts to "measure" their productivity and reluctant to give up their academic freedom in teaching as well as research, academics may take some persuading if the MMG's recommendations on the higher education curriculum are to be implemented in the future. If the MMG is to succeed, the demand on teachers' time has to be minimal and all interested parties — employers, academics, and other educational initiatives — have to agree to push in the same direction.
The MMG programme's focus on careers is absolutely essential and its careers activities will fill a gaping hole in maths education. There is no doubt that maths is widely perceived as irrelevant and that many a bright student is turned away from it by a perceived lack of career options. But there is one thing that should not be forgotten in all this: that the applicability of maths is only one side of the coin. Ask people who enjoy maths — be they school or university students, teachers, industrial or research mathematicians, or amateurs — and many of them will tell you that what turns them on to maths is not the fact that you can use it to build jet engines or encrypt credit card details. Or indeed that it offers a wide range of career options. It's maths in its own right that attracts them, its inherent beauty and the challenges it poses to their powers of abstraction and creativity. Someone who does not appreciate these will never be convinced by the promise of a large pay-packet and high-flying career. Conversely, someone who does appreciate it may well be turned off by too much talk of race car design and future mortgage payments. To reach the widest-possible range of students, both the practical and the esoteric side of maths have to be emphasised equally.