As we saw in Games people play from issue 27 of Plus, mathematical techniques have been applied very successfully to analysing certain types of games. The two examples that we looked at were the simple subtraction game Nim, and the much more complex case of chess endgames. The next step is to see how computers, which are no more than automated maths machines, are being programmed to actually play chess themselves.
Although it may be inevitable that computers will become unbeatable in the near future, human Grandmasters are still holding their own against the machines today. How is it, then, that the human brain, with a mere fraction of a computer's number-crunching ability, is still able to put up a good fight? The answer lies in the difference between human and artificial methods of reckoning, and smart players knowing how best to exploit computers' weaknesses.
The origins of chess

The Chess Game, by Ludwig Deutsch
Shaturanga, the ancestor of all chess-like games, is thought to have been developed around 1,600 years ago by an Indian philosopher. Since then it has spread across the globe, and evolved into several distinct forms, with China, Japan, Korea, Thailand and Europe all playing similar but distinct games throughout the middle ages. European chess underwent its most important development around 1475 when the capabilities of several of the pieces were changed. The fers became the most powerful piece on the board, combining the moves of the bishop and the rook, and was renamed the queen. Some of today's most familiar rules were also introduced then, such as castling, the two-square pawn advance, and en passant.
It was not for another 250 years, however, that anyone would publish a thorough and systematic discourse on the strategies of European chess. L'analyze des Áchecs, written by François-André Philidor in 1748, introduced concepts such as preventative moves and positional sacrifice, and included a study of basic endgames. This book was crucial in the development of the field of chess analysis and its nomenclature, which now includes such exotic terms as stonewall defences, chameleon variations, Noah's traps and Najdorf poisoned pawns.
Talking about a revolution
International-level players will spend hours thinking about a single position during a game, and spend their entire careers analysing and perfecting tactics for the "opening" first few moves. But the game is now undergoing another revolution. The processing power of computers has been increasing exponentially since the 1950s when the first chess-playing programs appeared. By the mid-80s computers were approaching Grandmaster level, and in 1997 Garry Kasparov, then World Champion, very famously lost an entire match to the IBM supercomputer Deep Blue (the computer won two games, lost one and drew the other three). It is only a matter of time before the machines become absolutely unbeatable, but even Kasparov himself is optimistic about the future for human players, who can use computers as excellent learning tools or in preparing for matches.
In the lingo of game theory (some of which we met in Games people play), chess is a finite game with no random element, played between two players each with complete information. It is also zero-sum, which means that one player's gain or advantage is necessarily to the opponent's detriment. As a consequence, it is theoretically possible to play a perfect game of chess - that is, both players could always work out the exact sequence of optimum moves, right through to checkmate. When playing such a perfect game, a player would always know the best move to make regardless of how the opponent responded, which in turn could also always be predicted. The entire game would be transparent, with both players knowing exactly how the game would end 10, 30, or 100 moves in advance.
It may be rational - but is it fun?
For example, at the start of a game of noughts-and-crosses there is a choice between nine permissible moves. Only 512 (29) different arrays of 0s and Xs can be made on a 3x3 grid, although the maximum number of games is actually less since rotational symmetry ensures some games are effectively identical. Also, of course, many of these arrangements are wins and so finish before all nine squares are filled. You can therefore know all possible games, and so be able to play the optimum response to any move from your opponent. In noughts-and-crosses, a draw is the only result possible between two rational players.
Chess, however, is almost inconceivably more complex, and the pieces can be arranged on the 64 squares of the board in 1044 distinct ways. One mathematician has calculated that there are about 10(1050) different legal games, which is far more than the number of particles in the entire visible universe. This is effectively an infinite number of permutations, and so in all practical senses it is impossible to play chess perfectly. Unlike the simple game of Nim described in Games people play, it is not known whether chess is a first or second-player win. It has not even been proved whether either player can in fact force a win, and so a game played between two omniscient beings may be fated to be a draw from the very start.
In terms of the Combinatorial Game Theory terminology described in Games people play, it is not known whether the value of a chess game is fuzzy, or whether the start is a zero position. In fact, this may be the exact reason why "God does not play games", to misquote Einstein slightly (he actually said "God does not play dice", expressing his disbelief in the unpredictability inherent in Quantum Mechanics). He may simply know the outcome to any game before it has even started, and then where would be the fun?

The 20 legal initial moves for White
From most positions the player will have a choice of which piece to move, and often also which square to move it to. From the initial position White can choose between only 20 legal moves, but this balloons into many hundreds of possibilities, or "candidates", in the middle game when more pieces have freedom of movement. The progression of a game can therefore be thought of as a flourishing bush, with numerous twigs coming off the same branching point to indicate each of the separate legal moves available from one position. At the next turn, each of these twigs itself branches off into many possibilities. As you look "deeper" into a position (that is, as you look a greater number of moves ahead), the number of possibilities that must be analysed increases exponentially. So the trick to playing chess efficiently is quickly to ignore lines of play that don't seem to improve your position, and to focus your analysis on a few promising candidates in order to "prune the game-tree". The computation is especially difficult because you must find a move that not only serves you well, but that also limits the good options available to your opponent. The crux of the difference between humans and machines is the disparate ways that we prune this tree.
Who is the better gardener?
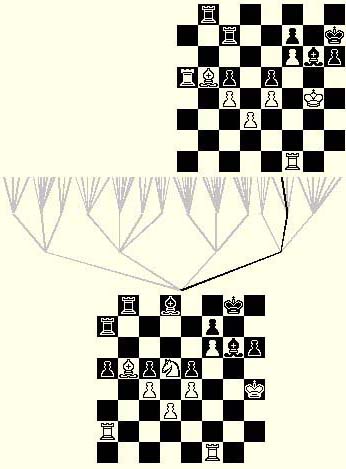
A simplified search tree for Black, with all but one line-of-play being discarded. The position is from one of the famous games between the computer Deep Blue, playing as Black, and World Champion Garry Kasparov in 1997
The brain of an experienced player seems to be able to prune the search-tree almost intuitively, and Grandmasters typically study only a handful of candidates at a position. This extremely effective focusing means that those lines selected can be studied to a great depth. Skilled players have a good sense of "boardfeel": without explicitly analysing a position they can spot which pieces are in commanding locations, which pawn structures are strong, where there are weaknesses in the opponent's formation, and so on. Computers play like a human novice, albeit one that can check millions of moves a second. They apply a "brute force" technique to playing chess, and have no conception of this abstract boardfeel. A computer can only wander blindly along the branches of the search tree, until it stumbles across a sequence of moves that may prove beneficial. A good human player, however, will identify a threat or an objective and will think laterally and inventively about how to use the available pieces in a combined way to achieve the desired result.
Although the programmed procedures, or algorithms, that computers use to reduce the search-space are being developed all the time, this is still the weakest aspect of a chess-playing computer. There are another two methods that programmers use to improve a machine's game. The first is an "opening library" that contains established sequences of moves for the first few turns. This received wisdom is the result of centuries of analysis of the best way to advance your pieces in the earliest stage of a game.

Computer investigations have shown that it is possible for White to capture one of the Black knights safely and ensure an eventual win
The second method is known as a "bottom-up approach". Many scenarios in the endgame are known to be an enforceable win for one of the players, such as a lone king versus a queen, or two rooks, or a rook and pawn against a bishop. A computer can then "unmove" pieces, or step backwards, to find all the positions from which these known wins can be reached.
This approach has produced enormous endgame databases so that if a computer aims for one of the included positions it can then play an essentially perfect game. All endgames with less than six pieces have already been analysed exhaustively. On the whole these computer investigations have agreed with the analyses of chess masters through the centuries. Some surprising results have been found,
however, such as for the endgame of rook and knight versus two knights. This is generally assumed to be a drawn game, but from a few special positions it is possible for White to capture one of the knights safely and ensure an eventual win. The position shown here requires the longest known sequence before capture: 243 moves. However, this exact position is very unlikely to arise, and a real game
would be ended by the 50-move rule, which states a game is a draw if 50 moves pass without a single capture or promotion.
Chinook and draughts
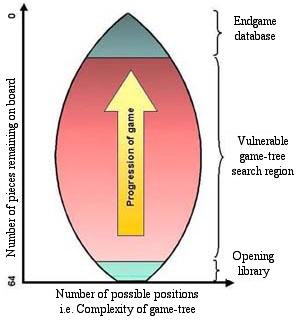
The region of game-play where humans still have some advantage
As can be seen in the diagram to the right, it is only really while in the region between leaving the opening library and entering the endgame database that a computer must rely on inefficient game-tree searches. This is when the pattern-spotting and inventiveness of the human mind is most at an advantage, and computers make the mistakes that may lose them the game.
This three-pronged attack of efficient search algorithms, opening libraries and endgame databases has already been applied extremely successfully to draughts (also known as checkers in North America). A program named Chinook recently played 220 games against draughts Grandmasters and won all but one. Machines have therefore already effectively achieved invincibility in this simpler game. Draughts has "only" 1018 legally-reachable game positions, and Chinook's database of all 400,000 billion positions with eight or fewer pieces ensures that it can play perfectly for a fair proportion of the game. On the occasion that it did lose, its human opponent forced the program out of its opening library very early, and so it had to spend more time in the vulnerable region before the endgame database. Chinook could not calculate to the depths of twenty-five moves that were required, and so lost. But Chinook is improving all the time, and the day that it loses its last game ever will soon arrive. In the not-too-distant future Chinook's database may cover all legal positions so that the program can play mathematically perfectly throughout the entire game. It will then have "solved" draughts.
The additional complexity of chess means that computers are not quite at this level of invincibility. But if even a standard home computer can now analyse more positions over the course of one game than the average player sees in a lifetime how is it even feasible for humans to still win? As mentioned before, computers are not intelligent players, and lack the creativity of a human mind. It is possible to study a computer's style of playing and so work out its strengths and weaknesses and play to them. Human players also have several other tricks up their sleeves.
Tactics for beating a computer at chess
Because a computer relies on a strictly mathematical, brute force approach in the middle game it can see only a limited number of moves in advance and is oblivious to patterns or general manoeuvres. This short-sightedness is known as the horizon, and as long as a human player makes no direct threats that are within the computer's horizon, it is unaware of the danger. The human can lure the computer into a devastating trap, or slowly prepare an overwhelming assault and only strike when it is too late for the computer to defend itself effectively.Another tactic that human players have successfully used takes advantage of the fact that a computer may assess positions in the game as if they have only just arisen. It will analyse millions of branches in the game tree all over again, even if it has seen an almost identical position very recently. A human will recognise that some moves hardly change the situation, and so will not bother reanalysing it. This difference can be exploited in clocked games where the players must make all of their moves within a specified time limit. The human can sometimes win simply by moving a piece back and forth between the same two squares, and the computer wastes all of its time re-examining each position.
Another common tactic in a timed game is to play quick moves that are mediocre but probably safe in that they don't lose you a piece or leave you open to checkmate. An especially effective move is one that complicates the position on the board and looks as if it could be part of an elaborate attack. The computer cannot know that this is what you are trying, and so will devote a lot of its time carefully analysing the position. This is known as the enough rope principle.
Trees and horizons

The horizon effect is becoming less important as faster processors and more efficient tree-pruning algorithms are developed. But the better programs may be susceptible to the inverse problem. This position comes from a game between a human playing as White against a computer. White has just placed the Black king in check with his queen on a8. The computer moved its rook to e8 and the audience laughed, thinking the program must have malfunctioned to play such a feeble move. Although the check has been blocked, the rook is completely undefended and the White queen can immediately capture this valuable piece. The more natural response might be to move the king out of check to g7 instead. It wasn't until the program was tested later that an explanation was found. The machine had realised that if the king moved to g7 then it would be unable to prevent White forcing an elegant checkmate five moves later.
But by sacrificing the rook checkmate is delayed, which the computer assessed as a gain. Any human player, however, would have moved the king anyway, because there is the chance that an imperfect opponent might not have seen this mating sequence. Sacrificing the rook is suicidal and effectively throws away the game. So, paradoxically, in certain situations a computer would perform better against humans if it played what it knew to be a weaker move!
As we've seen, then, programming a computer to play chess is a natural extension to using maths to analyse positions. Chess is inconceivably mathematically complex, and yet both humans and computers are able to play, although by using very different methods. Despite a computer's raw calculating power, human intelligence can still outwit the machines during the middle game. Our time is already up with draughts, however, and computers are close to solving the game.
But don't tell that to your PC, or it'll get far too big for its boot disk.
About this article

Lewis Dartnell read Biological Sciences at Queen's College, Oxford. He took a year off to travel, but has now just started a four-year MRes/PhD program in Bioinformatics at University College London's Centre for multidisciplinary science, CoMPLEX. In 2003 he came second in the THES/OUP science writing competition with an article on the parallels between language and the structure of proteins.