High roller solution

Share this page
Submitted by plusadmin on 1 November, 2004
November 2004

High roller

chessboard with coins

What is the probability, if you roll a coin across a chessboard and it comes to rest on the board, that it covers some corner of one of the grid squares?

(You can assume that the diameter of the coin is less than the sidelength of a single square on the chessboard.)


The solution

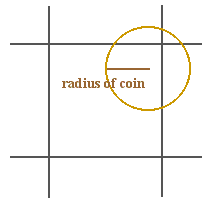
Suppose you randomly roll a coin (with radius $r$ ) across a chessboard (with squares with sidelength $s$ ) many times. What proportion of the time will it land covering a corner of one of the squares?

To cover a corner, the coin's centre must be less than the length of its radius away from the corner.


As the coin is equally likely to land with its centre in any position in the square, the probability it will land with its centre in the shaded region and hence cover a corner is the ratio of the coin's area to the area of a square on the board: 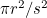$\pi r^2/s^2$, where $r$ is the radius of the coin and $s$ is the sidelength of a square of the chessboard.


Back to main puzzle page