
A knight's nightmare
Imagine a chess board with 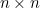 squares,
squares, 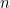 on each side. Now imagine a knight moving around the board - only using the moves that are allowed to a knight of course - so that each square of the board is visited exactly once, and so that the knight ends up on the same square as it started. Such a tour is called a closed knight's tour (it's closed because
the knight ends where it started). If you start experimenting on an ordinary chess board, you'll soon see that it's no easy feat to find a closed knight's tour. People have been entertaining themselves with this pursuit for centuries. The earliest recorded example of a knight's tour on the ordinary
on each side. Now imagine a knight moving around the board - only using the moves that are allowed to a knight of course - so that each square of the board is visited exactly once, and so that the knight ends up on the same square as it started. Such a tour is called a closed knight's tour (it's closed because
the knight ends where it started). If you start experimenting on an ordinary chess board, you'll soon see that it's no easy feat to find a closed knight's tour. People have been entertaining themselves with this pursuit for centuries. The earliest recorded example of a knight's tour on the ordinary 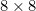 board came from al-Adli ar-Rumi, who lived in Baghdad around 840AD.
There are also example of knight's tours of But no-one has ever found a closed knight's tour on an
board came from al-Adli ar-Rumi, who lived in Baghdad around 840AD.
There are also example of knight's tours of But no-one has ever found a closed knight's tour on an 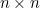 board when
board when 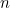 is odd. Can you prove why this is, in fact, impossible? Hint
is odd. Can you prove why this is, in fact, impossible? Hint
If you're poetically minded, try this one: find a knight's tour on this 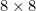 board, so that the syllables on the squares, when read in the sequence of the tour, form a verse (note that this time you're not asked for a closed knight's tour - it does not have to end at the same place it started). Hint
board, so that the syllables on the squares, when read in the sequence of the tour, form a verse (note that this time you're not asked for a closed knight's tour - it does not have to end at the same place it started). Hint
This puzzle was published in 1884 in the book Chess Fruits by T. B. Rowlands and his wife Frideswide F. Rowlands. Crossword puzzles had not been invented at that time, and this kind of puzzle was very popular. If you are stumped by last issue's puzzle, here is the solution. For some challenging mathematical puzzles, see the NRICH puzzles from this month or last month. |