Communication is an amazing thing: within our minds we carry a kaleidoscope of thoughts and ideas, yet when we try to convey them, all we can do is say one word at a time. Our many-dimensional world of thought has to be reduced to a one-dimensional string of words. Communicating complex ideas in such a linear framework is only possible because our mind can endow our words with structure and allow us to pick up this structure when we listen to someone speak or read a text. Linguists and philosopher have long suspected that the structures within language are intimately wound up with the evolutionary processes that have turned us into what we are now.
Get your head around this.
What is needed are theoretical tools to understand language. Maths is of course a prime candidate when it comes to spotting structure, but finding a mathematical model that can accurately describe language is no easy feat. A speech or a text is much more than the sum of its individual components — its words. How do you capture mathematically the moment when a collection of words turns into a concept or an idea? And how do you trace the development and interaction of ideas as the narrative progresses?
Various mathematical techniques have been used to analyse texts in the past, but recently a team of physicists and language researchers, led by Elisha Moses of the Weizmann Institute in Israel and Jean-Pierre Eckmann of the University of Geneva, have refined an existing model in a way that seems to do the trick rather well. To prove the point they applied their model to twelve of the most acclaimed texts of Western culture, including War and Peace by Tolstoi, Shakespeare's Hamlet, Don Quixote by Cervantes and Kafka's The Metamorphosis, as well as the scientific and philosophical works Relativity: The scpecial and the general theory by Einstein, The Critique of Pure Reason by Kant and Plato's The Republic.
Their technique does seem to be able to spot the ideas that lie at the heart of each book, and can trace the way they interact and develop. It even allows them to identify linguistic structures that seem to be essential in helping our minds and memories reconstruct the author's multi-dimensional world of ideas from the one-dimensional string of words on the page.
Their model is worth describing not only because it is useful, but also because it is amazingly elegant. It turns each book into a space with many dimensions in which each direction corresponds to a central idea. The narrative meanders through this conceptual forest and the path it traces out serves to understand the structure of the text.
To understand the maths behind this, let's start with the ordinary three-dimensional space equipped with the usual Cartesian co-ordinate system formed by the x, y and z axes. The three basic directions here can be described by three arrows, each being one unit long. One arrow indicates the direction of the x-axis, one the direction of the y-axis and one the direction of the z-axis. Technically, these arrows are called vectors and they can be represented by the triples $$ e_1= \left( \begin{array}{c} 1 \\ 0\\ 0\\ \end{array} \right), e_2=\left( \begin{array}{c} 0 \\ 1\\ 0\\\end{array}\right), e_3=\left( \begin{array}{c} 0 \\ 0\\ 1\\ \end{array} \right).$$
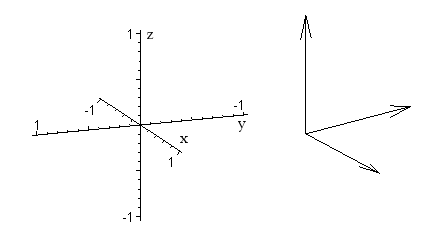
The image on the left shows the co-ordinate axes and the image on the right shows the vectors e1, e2 and e3.
Similarly, any other direction can be represented by a vector $$ v = \left( \begin{array}{c} a \\ b\\ c\\ \end{array} \right)$$ which simply means "the direction indicated by an arrow starting at the point with co-ordinates (0,0,0) and ending at the point with co-ordinates (a,b,c)". The important thing to notice here is that this vector v, no matter what its entries a, b and c are, can be expressed as a combination of the initial three vectors: if you start at the point with co-ordinates (0,0,0), then move a steps in the direction indicated by e1, then b steps in the direction indicated by e2 and finally c steps in the direction indicated by e3, then you end at the point with co-ordinates (a,b,c) and have indicated the arrow v. This can be written as a formula: $$ v = a e_1 + be_2 + c e_3.$$
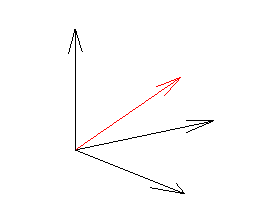
The red arrow represents a vector pointing from the point (0,0,0) to the point (0.6,0.5,0.6).
Now suppose you have a text, one of the books mentioned above for example, which contains some number N of different words. You can label these words by the symbols w1 through to wN. Next, represent each word by a vector which has N entries (rather than just three as in our example): the word w1 is represented by the vector with a 1 as its first entry and 0s for the other N-1 entries, the word w2 is represented by the vector with a 1 as its second entry and 0s for all the other entries, etc. What you have now is an N-dimensional space in which each of the basic directions represents a word. (Simply ignore, for the moment, that you can't visualise more than three dimensions!)
Any combination of words now defines an arrow, or vector, in the space. As an example, take the text "I love you" consisting of three different words. If you assign to the word "I" the vector $$e_1= \left( \begin{array}{c} 1 \\ 0\\ 0\\ \end{array} \right),$$ to the word "love" the vector $$e_2=\left( \begin{array}{c} 0 \\ 1\\ 0\\ \end{array} \right)$$ and to the word "you" the vector $$e_3= \left( \begin{array}{c} 0 \\ 0\\ 1\\ \end{array} \right),$$ then the pair of words "I" and "love" are represented by the vector $$e_1 + e_2 = \left( \begin{array}{c} 1 \\ 1\\ 0\\ \end{array}\right),$$ the pair of words "love" and "you" by the vector $$e_2 + e_3 = \left(\begin{array}{c} 0 \\ 1\\ 1\\ \end{array} \right),$$ and the pair of words "I" and "you" by the vector $$e_1 + e_3 = \left( \begin{array}{c} 1 \\ 0\\ 1\\ \end{array} \right).$$
Now that the text is represented as a mathematical space, the scientists' model sets out to identify combinations of words that together from concepts. It does this by checking which words occur together in chunks of text that are 200 words in length — this, according to the scientists, is about the amount of words that a reader can be aware of at any given moment.
After eliminating "meaningless" words such as pronouns, and performing some clever tricks to ensure that coincidental combinations of words are filtered out, the model is left with prime candidates for combinations that form concepts. This concept-spotting process seems to work rather well, as an example from Einstein's book shows: one of the combinations of words that features most strongly hints directly at the applications of relativity to astrophysics:
Since each concept is just a combination of words, it defines a vector in our N-dimensional word space. In fact, using some clever algebraic tricks, these concept vectors together can be taken to define a smaller space, sitting within the space of all words. As an analogy, take the text "I love you" again, and see how the vectors representing the pairs "I love" and "love you" together define a plane, which sits within in the three-dimensional space we started with.
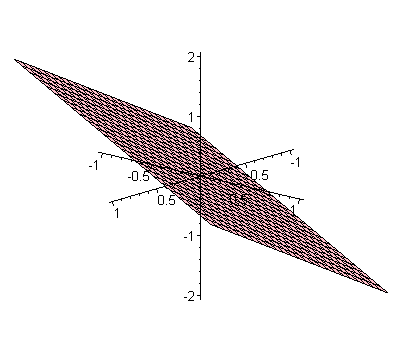
The plane defined by the two vectors e1+e2 and e2+e3.
And there we have it: a geometric representation of all the concepts that occur within the text. It is a smaller space sitting within the space of all words, much like a plane sits within three-dimensional space. Each concept corresponds to a fundamental direction within this subspace, in other words it corresponds to the higher dimensional analogues of our three vectors e1, e2 and e3 of the example.
The narrative of the text now also has a geometric meaning. As a reader reads through the text, he or she will be aware of all the words that appear in chunks of about 200 words in length. These 200 word combinations each form a vector in the space of all words, which can be projected onto our subspace of concepts. The tips of these attention vectors move through the concept space and trace out a path within it as the 200 word window of attention slides across the text. The path meanders through the space as the narrative develops, taking up different directions that represent the various topics and concepts the text touches upon.
But what can this path tell us? A statistical analysis of its progression showed the scientists that its movement is far from random. Relationships between concepts develop and persist as the reader reads through the text, and, as far as their statistics are concerned, they do so in a very similar way in all of the books considered. The structures that force the narratives' path very likely form the scaffolding from which a reader can reconstruct the author's complex thoughts.
The scientists' results suggest that these structures are hierarchical in nature. An obvious candidate would be the subdivision of each work into volumes, of each volume into chapters, of each chapter into paragraphs and each paragraph into sentences. Further tests carried out by the scientists showed that it is indeed this hierarchy that seems to stop the narrative path from going random.
This may not sound very surprising: after all, there must be a reason why we tend to subdivide our streams of words into sections, paragraphs and sentences. But what this study indicates is that these hierarchies are not just convinient for some superficial reason, but may form the essential underpinnings of language. The doors opening the way between the world inside us and the world around us may well hinge upon them.