
Tying it all up
As above, so below
To mediaeval thinkers, the universe was divided into two realms, the earthly and the heavenly. These realms were thought to operate quite differently, and it was Newton who brought the two together, claiming that "as above, so below" - that what holds in one part of the universe and at one scale, holds everywhere and at every scale.
As above, so below. Newton saw that the same force caused apples to fall on earth and the planets to rotate. [Images of Jupiter and her moons courtesy of NASA]
At the scale and speed of everyday life, we still use Newton's concepts of force, matter and motion. However, they have proved to be inadequate at both the very small (subatomic) and very large (cosmological) scales. Like mediaeval thinkers, we use different laws depending on whether what we are looking at is small or big - we use quantum mechanics to describe what happens at the very small scale, and general relativity to describe what happens on the large scale, where quantum effects can be ignored. General relativity is Einstein's theory of gravity, replacing Newton's 300 year old theory, and unifying gravity and the geometry of space-time.
But although the whole paraphernalia of modern technology relies on the understanding these two theories bring, they are mutually incompatible, because noone knows how to reconcile gravity with quantum mechanics. This means we can't provide a good description of what happens in situations where both gravity and quantum effects are important. So physicists are still seeking for their Holy
Grail, a so-called "theory of everything", which would combine relativity and quantum mechanics. The current hot contender is known as string theory.
A quantum theory of gravity
Probably one of the most widely-known statements from quantum mechanics is the Heisenberg uncertainty principle. This is the principle that, at the very tiny (quantum) scale, position and momentum cannot simultaneously be known arbitrarily accurately - the more accurately one is known, the less accurate it is possible to be about the other.Suppose we try to find out what is happening in a very tiny region of what classically has been thought of as "empty space". The smaller the region, the more accurate we are being about position, and therefore the less accurate it is possible to be about momentum, and therefore energy. This means that at very tiny scales, energy - and therefore mass, because E=mc2 - fluctuates enormously. At about 100th the size of the nucleus of an atom, electron-positron pairs start to pop in and out of existence, and this energy fluctuation first becomes appreciable. At even tinier scales this fluctuation is so big that there is enough energy/mass inside this tiny region to make a black hole. So what used to be thought of as a vacuum is actually a seething mass of activity - "empty space" is really a foaming sea of minute black holes popping in and out of existence. This "foam" isn't something that sits inside space and time - it is space-time itself. Since gravity cannot possibly be ignored in the presence of black holes, our current understanding of gravity cannot be reconciled with quantum mechanics.

Empty space is really a foaming sea. [Image from www.freeimages.co.uk]
Physicists hope that a new theory of quantum gravity will emerge, which can describe these small-scale properties of space-time. There is a precedent. Until the 1940's, similar problems appeared when physicists attempted to reconcile electromagnetism and quantum mechanics. But this reconciliation has been carried out successfully, in the theory of quantum electrodynamics, which glories in the auspicious acronym of QED. Calculations in QED are carried out via "Feynman diagrams" which are successive approximations to QED. These are such excellent approximations that they give the most accurate numbers in the whole of science.

A first-order Feynman diagram
The Feynman diagram to the right represents the simplest approximation to what happens when a (negatively charged) electron and a (positively charged) positron collide. The two particles are annihilated, resulting in the formation of a photon, and the subsequent formation of a new electron-positron pair.
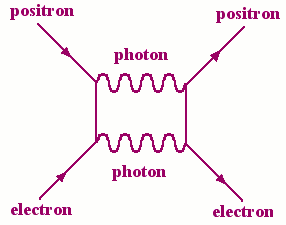
A second-order Feynman diagram
The first correction to this approximation is represented on the right. Two photons are created and annihilated.
And so on. Although the successive calculations very quickly become very difficult, the approximations are so accurate that physicists hardly ever have to do more than the first one or two. But noone knows how to approximate gravitational interactions in the same sort of way. The difficulty arises because in Feynman diagrams, there are "special points" where particles are created and annihilated. In mathematical language, the diagrams are graphs, and problems arise at the nodes of the graphs. Physicists know how to solve these problems when approximating electromagnetic interactions, but the corresponding series of approximations for gravity leads to insuperable difficulties.
The origins of string theory
Although the origins of string theory are convoluted, the main continuing motivation is the attempt to reconcile gravity with quantum mechanics by thinking of particles as something larger than points. The new ingredient in string theory is that particles are no longer thought of as "pointlike", but instead as "stringlike" - 1-dimensional rather than 0-dimensional. The non-zero size of these "strings" should alter the physics of very short distances, thereby sidestepping the problems encountered in quantum gravity.
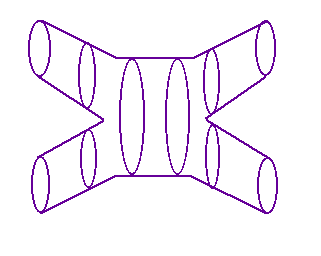
A first-order string diagram
Feynman diagrams are approximations to the known theory of QED - but suppose we blindly draw the analogous diagrams with particles represented as strings instead of points. We don't know the theory we are approximating, but let's go ahead and do it anyway. Interactions will be represented by strings combining and dividing. The string diagram to the right is analogous to the first Feynman diagram drawn above. Two strings combine to form one, which then divides into two.
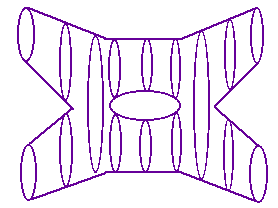
A second-order string diagram
In the second-order string diagram to the right, the two strings combine and divide twice.
Immediately some miraculous things happen.
Firstly, there are no "special points" in string diagrams, as there are in Feynman diagrams. So these diagrams sidestep the problems that arise when physicists attempt to approximate gravitational interactions. Also, although it may seem surprising, string diagrams are mathematically much simpler than Feynman diagrams. Rather than being graphs with nodes, they are 2-dimensional smooth surfaces - and there are far fewer smooth surfaces than there are graphs.
The other important feature of string theory is that because strings are 1-dimensional objects, they can be in infinitely many states, unlike 0-dimensional points, which can only be in one. A major issue in physics is understanding how to unify all particles, and in principle string theory might provide a way to do this, with all particles appearing as different states of the fundamental string.
Another very attractive feature of these diagrams is that since the strings are so tiny, for many purposes they can be thought of as points, and so no successes of QED are lost. There is just one problem. Feynman diagrams are highly accurate approximations to the known theory of QED. But noone knows what theory these string diagrams are meant to approximate!
Strings 2002
![[Image: Strings 2002 participants]](/issue21/features/strings/group.jpg)
Strings 2002 participants [Photo and copyright Anna N. Zytkow]
This summer pretty much the entire strings community (around 450 scientists) gathered in Cambridge for the Strings 2002 conference, and Plus spoke to some of them. There was a huge sense of optimism among the participants, a confidence that soon physics will be able to answer the most fundamental questions, to get to the heart of things. One physicist told us that "physics is now approaching the level where it acquires the ability to answer philosophical questions. For thousands of years people have asked questions like 'what is time?' 'what is space?' 'what is reality?'. However, their language was limited - they didn't use the language of maths - and as a result they couldn't even come close to the reality which we see now in physics. This reality cannot be explained in ordinary language, just as you cannot explain complicated feelings using primitive language."
![[Image: Stephen Hawking]](/issue21/features/strings/hawking.jpg)
Stephen Hawking at Strings 2002
[Photo and copyright Anna N. Zytkow]
These researchers feel that they are nearing the goal of physics, which is to understand the meaning of space, time and causality. In reaching this goal, the role of mathematics is enormous - not only is it needed to answer questions, but also to ask them.
A counterintuitive fact - and one that might at first glance rule out string theory as a candidate for a good model for our universe - is that it requires spacetime to have several extra dimensions (six in the simplest version). You may have noticed that we appear to live in a four-dimensional world, with three space dimensions and one time...!
Dimensions to spare
![[Image: Constantin Bachas]](/issue21/features/strings/bachas.jpg)
Constantin Bachas speaking at Strings 2002
[Photo and copyright Anna N. Zytkow]
It is thought that we don't directly experience these extra dimensions because they are rolled up incredibly tightly on themselves. Constantin Bachas, a researcher at the Ecole Normale in Paris, says that a useful analogy is that of a hosepipe. "Suppose you live on a very thin hose - it's very hard to experience the fact that there is one more dimension. You basically see one very large dimension [the length of the hose] in which you are moving, and then you need a very fine resolution to see the extra dimension."
Things are complicated by the fact that the extra dimensions are at such a small scale that quantum uncertainty comes into play. "What makes it hard to speak about this in classical terms as opposed to quantum mechanical terms is that the precise sense in which these extra dimensions cannot be sensed or detected is that the quantum mechanical wave function is spread around them - so in other words there is equal probability of being in any single position on these extra dimensions, and as a result we just cannot sense them, we cannot do any measurements that are local in these extra dimensions. Classically it's hard to have something spread over a dimension, but quantum mechanically this can very well happen."
The thinking is that the six extra dimensions of string theory are rolled up incredibly tightly. The exact way in which these unwanted spacetime dimensions are rolled up (called compactification) is an exciting area of geometry, and one where pure mathematicians contribute. You might imagine you could just roll all the unwanted dimensions up, one at a time, in the same way that you roll up a long thin rectangle to make a hose. But if you do this, you end up with a strange surface with lots of holes, like a crazy ten-dimensional doughnut, and the properties of this surface stop it from being a good candidate for compactification.
![[Image: Michael Atiyah]](/issue21/features/strings/atiyah.jpg)
Sir Michael Atiyah at Strings 2002
[Photo and copyright Anna N. Zytkow]
Fields medallist Sir Michael Atiyah is a pure mathematician who has been collaborating with physicists for more than twenty years. He says that although string theory attempts to describe the fundamental laws of physics, "it has become highly sophisticated mathematically. And one of the big surprises is that it's using a vast amount of the modern mathematical machinery of geometry I and others have been studying for a long time. And not only are physicists using this mathematics, but the ideas of physics are generating a lot of new ideas and results in geometry as well.
"Einstein's theory [of relativity] had to do with curvature of space; these other theories have to do with curvature of space with extra dimensions thrown in. In addition to space and time, people have ideas that there are extra, internal dimensions; things can move around inside and give you more degrees of freedom. The curvature of these [dimensions] which are of a very special type, are a part of mathematics."
A theory of everything

If string theory can be made to work, it will provide an unbelievably elegant "theory of everything". The reason is that one-dimensional things like strings can vibrate, in a way that zero-dimensional things (points) can't. Edward Witten, one of the leading researchers in the field, explains the idea thus. "If you have a violin string, or a piano string, it can oscillate with many different shapes. In the case of the strings that we use in this kind of string theory, the main thing that is important is that they also have many possible shapes of vibrations. And different elementary particles are interpreted as coming from the same string vibrating in different possible shapes. So the unification of the elementary particles arises from interpreting the electron, muon, proton, neutrino, and all those things as different ways that the same basic strings can vibrate."
Like others in the field, Constantin Bachas is very hopeful string theory can reconcile quantum mechanics and the theory of general relativity. He says there are many indications that the theory is on the right path. "There is no real formulation of the field yet, in a way in which one can derive all its consequences. For the moment we have glimpses, indications, but they all go in the right direction. [For example] it is a good quantum theory of gravity. The optimistic goal is that this would be a unified theory of all particles, of all interactions, and they are all different oscillation modes of a single fundamental string."
Strings, superstrings, and M-theory
![[Image: Edward Witten]](/issue21/features/strings/witten.jpg)
Edward Witten speaking at Strings 2002
[Photo and copyright Anna N. Zytkow]
Until recently, it was thought that there were five internally consistent string theories, which are now known as superstring theories. The preposition "super" refers to "supersymmetry", which means that for every known force-carrying particle there is a so-called superparticle; a mass-carrying "cousin". Superparticles haven't been observed experimentally, but this could be because they are just too heavy to be detected by current particle accelerators. Finding one of these particles would provide a very exciting indication that string theorists are on the right track.
Edward Witten says that if string theory works, "we'll be able to understand the real world a lot better. The fact is that the electron and muon mass and a lot of other things are measured but not understood. In practice we don't understand the theory nearly that well. The way we understand it now, we still have one important thing that's come out of it, which is suggested and is
searched for in experiments, and that is the prediction of supersymmetry, which is a kind of quantum structure in the nature of space-time, enriching Einstein's theory to incorporate quantum variables. If supersymmetry is right, then ordinary particles have cousins, the so-called superpartners, that arise when the particle vibrates in the new dimensions. So this is something that we look for at
accelerators."
![[Image: Edward Witten]](/issue21/features/strings/M-theory.jpg)
M-theory and the network of string theories [Image courtesy of Stephen Hawking]
One of the most exciting developments of the last decade has been the realisation that the five apparently distinct superstring theories are really different approximations to a single underlying theory - the so-called M-theory. M stands for mother (as in mother of all theories) or membrane, or mystery, or even matrix, depending on who you ask. Although some eminent scientists - for
example, Stephen Hawking - doubt that we will ever find a theory of everything, others are hopeful that M-theory will provide the unified framework in which physicists can gain a new understanding of the universe. Only time will tell who is right.
About this article
Helen Joyce is Editor of Plus.

Michael Green at Strings 2002
[Photo and
copyright Anna N. Zytkow]
When Helen was writing this article, Michael Green, a Professor of Theoretical Physics at the University of Cambridge and one of the organisers of Strings 2002, attempted the Herculean task of summarising all of quantum mechanics for her in two hours! She is very grateful, although she didn't quite manage to take it all in.
Helen also interviewed a number of participants in Strings 2002, which was held at the Cavendish Laboratory in Cambridge, July 15-20.
Dr. Anna N. Zytkow of the Institute of Astronomy in Cambridge very kindly allowed Plus to use photographs she took at Strings 2002.
Comments
Anonymous
First, I hope you are having a nice day. If not, I hope it gets better soon!
Although some of our greatest thinkers are still living, I appreciate your mentioning of Dr. Richard Feynman! Sadly, Dr. Feynman was not well appreciated at times because he was not "polished" and some said he didn't speak well when compared to other greats!
Interestingly, I am curious about Dr. Wheeler, but I believe I understand. It is impossible to mention all the Giants!
• http://www.physorg.com/news127476893.html
As a chemical engineering student, I enjoyed thermodynamics, non-ideal thermodynamics, and quantum mechanics. To quote my physical chemistry professor, entropy is like a slippery eel, when you think you have it grasped, it slips right out of your hands.
String theory is such an amazing field! I wish I had the mathematical skills to be of importance in such a magical time of discovery!
Thanks for the article!