Plus Advent Calendar Door #3: Why sine (and cosine) make waves
We had a wonderful time splashing about in waves when we were writing about a research programme that is currently taking place at the Isaac Newton Institute for Mathematical Sciences. But you might be surprised that our started with a triangle...
Think of a right-angled triangle. Then you'll probably remember from school that you can use the sine and cosine functions to find out more about the triangle. If $\alpha$ is one of the angles that isn't the right angle then you have $$ \sin(\alpha) = \frac{\mbox{length of opposite side}}{\mbox{length of hypotenuse}} $$ and $$ \cos(\alpha) =\frac{\mbox{length of adjacent side}}{\mbox{length of hypotenuse}}. $$
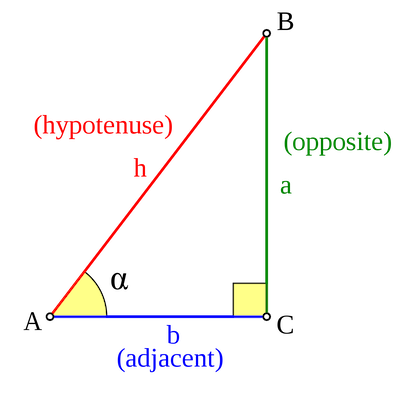
For the angle α, the sine gives the ratio of the length of the opposite side to the length of the hypotenuse. The cosine gives the ratio of the length of the adjacent side to the length of the hypotenuse. (Image by Dnu72 – CC BY-SA 3.0.)
The sine and the cosine functions can do a lot more than help you solve geometry problems. They can be used to build any waveform — the music you are listening to, the digital signal you are sending over wifi, even the swell on the sea — no matter how complicated these natural or human made oscillations might be.
Going round and round
The first step to constructing a wave is to imagine a circle of radius 1 drawn in Cartesian coordinates, with the centre of the circle lying at the point $(x,y)=(0,0).$ Imagine moving around the circle in an anticlockwise direction, starting at the right-most point, $(1,0)$. After you have rotated through an angle of $\alpha$ that is less than 90 degrees (corresponding to less than $\pi/2$ in radians) the point $(x,y)$ you are at defines a right-angled triangle, with corners $(0,0), (x,0)$ and $(x,y).$ The hypotenuse of this triangle has length 1 because the point $(x,y)$ lies on our circle of radius is 1. For this triangle we have $cos(\alpha)=x$ and $sin(\alpha)=y.$
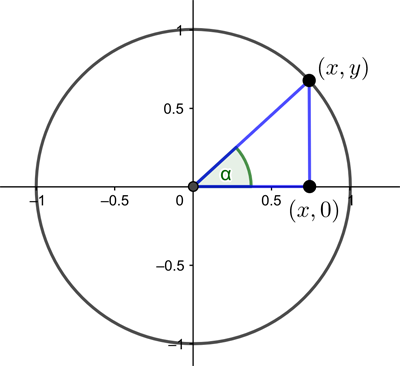
A right-angled triangle formed from a point on the unit circle.
You can continue to move around the circle anti-clockwise to make the angle $\alpha$ bigger than $\pi/2.$ When you do this, the triangle with corners $(0,0), (x,0)$ and $(x,y)$ no longer has $\alpha$ as one of its angles.
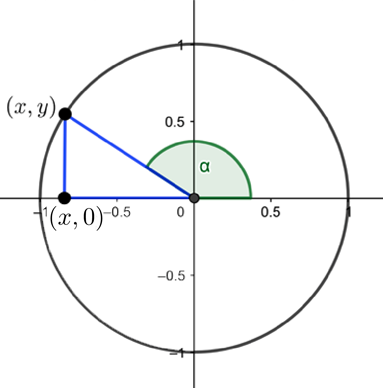
When α is greater than π/2, then the right-angled triangle formed from a point on the unit circle no longer contains the angle α.
However, there is nothing to stop you from extending the definitions of the sine and cosine of $\alpha$ in analogy with what we had before: $$\cos{(\alpha)}=x\;\;\;\;\mbox{and}\;\;\;\sin{(\alpha)}=y,$$ where $(x,y)$ are the coordinates of the point you are at.
What happens to the sine and cosine as you move once around the circle? In one circuit of the circle you will have turned through an angle of $2\pi$. As you moved around the circle your vertical coordinate (the sine) started at $0$ and increased steadily until it reached a maximum of $1$ when you were on top of the circle. As you kept moving it then dropped down to $0$ again in a symmetrical fashion, before reaching a minimum of $-1$, and finally coming back up again to 0.
If you plot how the vertical coordinate (in red in the figure below) varies with the angle turned through (from 0 to $2\pi$) you get a regular wave shape. It starts at 0, goes up to the maximum of 1, then down to 0 again, before dropping to the minimum of -1, and up again to 0.
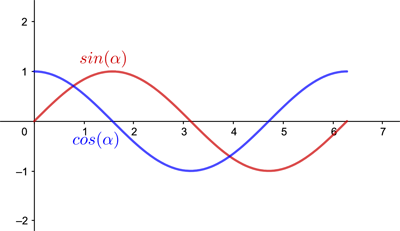
The red wave is the sine of the angle plotted against the angle (coming from the vertical coordinate) and the blue wave is the cosine of the angle plotted against the angle (coming from the horizontal coordinate).
This wave pattern repeats as you carry on going around your circle a second time, increasing the angle you turned through from $2\pi$ to $4\pi,$ and a third time travelling from $4\pi$ to $6\pi$, and so on. You end up with an infinitely long, perfectly regular wave. The horizontal coordinates (the cosine) give a similarly perfect wave (plotted in blue above), offset against the first one by a distance of $\pi/2$ along the horizontal axis. This extends our definition of the sine and cosine to angles greater than $\pi/2$. (You can also define the sine and cosine for negative numbers by going round the circle in a clockwise direction.)

The red wave is the sine of the angle plotted against the angle (coming from the vertical coordinate) and the blue wave is the cosine of the angle plotted against the angle (coming from the horizontal coordinate).
Explore how you can stretch, squeeze, speed up and slow down waves in the rest of this introductory article!
Return to the Plus advent calendar 2022.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
