
Bach and the musical torus
This article is a reprint of the American Mathematical Society Feature Column Surface Topology in Bach Canons, II: The Torus by Tony Phillips. It is based on work with Eric Altschuler, published in Musical Times in 2015.
A musical score as a topological space
Let's start by repeating some material from our previous article Bach and the musical Möbius strip. Topologically, a one-voice musical score is a two-dimensional strip. The horizontal (time) coordinate runs from start to finish; the vertical coordinate runs from lower pitches to higher pitches.
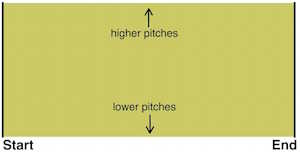
A one-voice musical score as a rectangular strip. Image: Tony Phillips.
If the score repeats exactly, then that time symmetry corresponds to identifying the left (start) and right (end) borders of the strip, forming a cylinder.
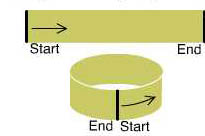
A repeating score is topologically a cylinder. Image: Tony Phillips.
Generally, the topology of musical scores is constrained to the cylinder (and the Möbius strip in the case of some canons using inversion, as discussed our previous article) because of the impossibility of looping back in the vertical (pitch) direction. There is, however, one example in which Johann Sebastian Bach plays on our perception of pitch and tonality to give a repeatable cycle of "upward" pitch changes. This is his Canon 5 from the Musical Offering (BWV 1079).
The Musical Offering
The Musical Offering is a work prepared by Bach after his visit to the court of King Frederick II of Prussia (Frederick the Great) in Potsdam on May 7, 1747. The King, who was himself a musician, proposed a theme on which Bach, on the spot, improvised a 3-part fugue.
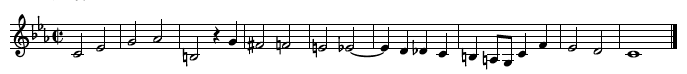
The Royal theme proposed to Bach by Frederick the Great. Note that it starts and ends on the same note. Click below to listen.
Frederick also challenged Bach to improvise a 6-part fugue on the theme, but, we are told, the composer declined this much more difficult task. When Bach returned home to Leipzig, he wrote out the fugue he had improvised, along with the 6-part fugue Frederick had requested, a trio sonata, and a set of ten canons, all based on the Royal theme. He had them printed up for the King: this was Bach's Musical Offering.
Canon 5
Canon 5 of the Musical Offering is scored for three voices. The highest voice (the ground) repeats, over and over, a version of the Royal theme. But Bach has modified the melodic line of the theme so that, instead of ending on the same note on which it started, it ends, and the next iteration starts, one full tone higher. So the first iteration starts on the note middle C and ends on D.
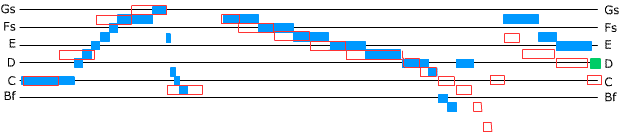
The ground for Canon 5, first iteration, and a graphic representation comparing it with the Royal theme (hollow boxes). The horizontal lines are non-standard: they are one whole tone (2 half-steps) apart, uniformly. The labels for the spaces between the lines, starting with the space below the bottom line and ending with the space above the top line, would be A, B, Df, Ef, F, G, and A. Fs represents F-sharp, etc., Bf is B-flat. Note that the Royal theme starts and ends on C, but the melodic line of the ground ends one full tone higher than it starts. Click below to listen.
The second iteration of the ground starts on D and ends on E.
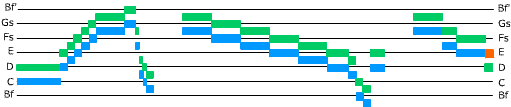
The first two iterations of the ground for Canon 5, with the same graphic conventions as above. Bf' represents the B-flat above middle C.
The third iteration starts on E and ends on F-sharp, and so forth.
The other two voices form a canon: one (the middle voice) imitates the other (the bottom voice) exactly, except one measure later and a fifth (7 half-steps) higher. The bottom voice starts on the C below middle C; the middle voice starts on the G below middle C, one measure later.
When the top voice (the ground) starts its next iteration, the two other voices also start repeating themselves, also one full tone higher: all three voices have shifted one full tone up.
An octave is 12 half-steps; so after six iterations the ground should end on the C above middle C (C, D, E, F-sharp, G-sharp, A-sharp — or equivalently B-flat —, C). The music seems to continue spiralling upwards, but this is an illusion: the ground drops back to middle C, and the whole process is back where it began.

All six iterations of the ground for Canon 5, with graphic conventions as above.
The music must be experienced. I recommend the excellent performance by Michael Monroe below. You can follow the score note by note on the video.
A sonogram of the Michael Monroe performance of Canon 5 shows that, despite the illusion that the pitch has continued to rise, the seventh iteration is on the same pitch as the first:
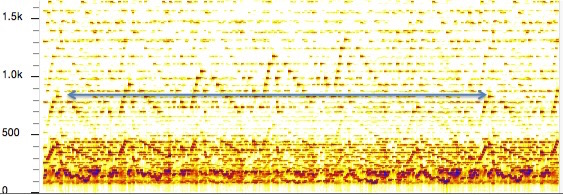
The illusion: pitch versus tonality
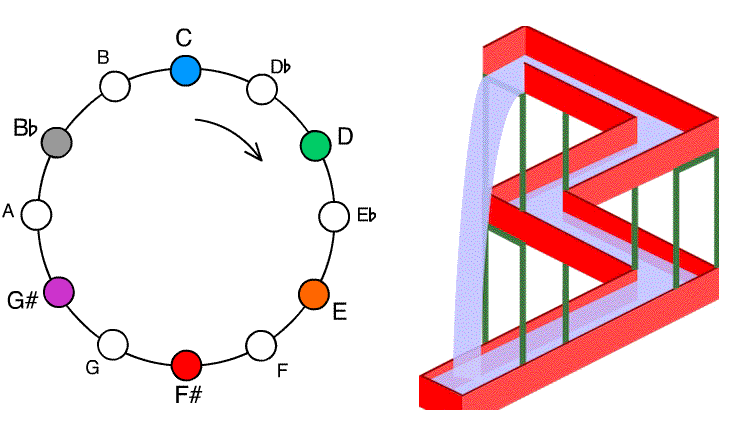
Bach is exploiting an aspect of human perception of sound: along with pitch (correlated with frequency, and therefore taking values along an ascending continuum) we are sensitive to tonality: in some essential way, middle C and the Cs above and below sound to us like the "same" note. So instead of a linear continuum, tonalities form a circle. This leads to a phenomenon called the Shepard scale where a musical sound seems to be rising in pitch, but yet ultimately goes nowhere. The effect can be mimicked on a piano:

These seven chords on the piano show how a rising sequence of tonalities gives the illusion of a rising sequence of pitches. In fact, the last chord is the same as the first. Click below to listen.
The discrete Shepard scale illusion is akin to the impossible waterfall depicted by M. C. Escher. The woodcut Waterfall is copyrighted, but Andrew Kepert has put in the public domain the rendering below of the conceptual core of Escher's woodcut.
Click here to listen.
The torus
If we agree to group the notes in the written-out Canon 5 ground by tonality rather than by pitch, the image of the six iterations, above, collapses into a rectangle:

Identifying pitches an octave apart as equivalent reduces the complete cycle of the Canon 5 ground to this configuration.
Since the top equivalence class (the space above the top line, representing pitch of A) is adjacent in tonality-space to the bottom one (the bottom line B-flat), and since the two ends are adjacent in time, the time-tonality space represented is a torus. Identifying left and right edges gives a cylinder:
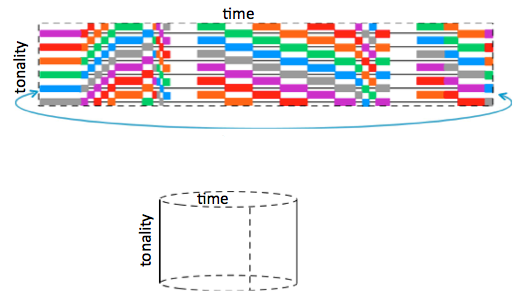
And identifying the top and bottom edge gives a torus.
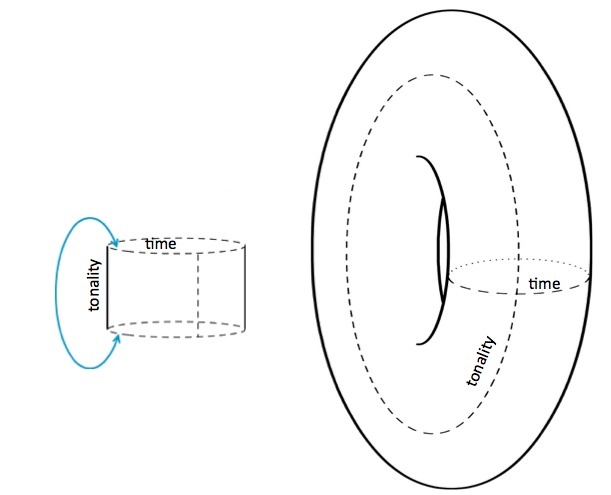
Note that our geometric picture of a smooth torus in three-dimensional space has points of positive and negative curvature. This does not make sense for a musical score. The score of Canon 5 is a flat torus, obtained by identifying opposite edges of a rectangle. It exists abstractly, but cannot be smoothly exhibited in three-dimensional space.
A flat torus.
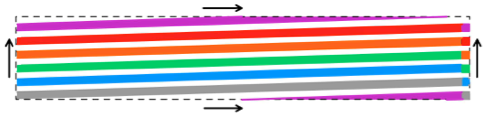
On the flat torus defined by the circle of tonalities and the (modulated) repeating of the ground, the melodic line of Canon 5 wraps six times in one direction, once in the other.
About this article
This article is a reprint of the American Mathematical Society Feature Column Surface Topology in Bach Canons, II: The Torus by Tony Phillips. It is based on work with Eric Altschuler, published in Musical Times in 2015.

Tony Phillips.
Tony Phillips is a John S. Toll Professor of Mathematics at Stony Brook University, specialising in topology. He has had a life-long interest in manifestations of mathematics in art.

Eric Altschuler.
Eric Altschuler is Associate Chief, Department of Physical Medicine and Rehabilitation, Metropolitan Hospital, New York City. He is a great lover of the music of JS Bach and student of Bach's exploration of the tonal and organisational systems of music.
Comments
Burger Man
Brilliant article. Exploring mathematics in music is very interesting, as these two areas rarely mingle with each other. Hopefully there would be more articles such as this, and cover other genre of music such as blues, jazz, or even rock music.
Marianne
Glad you liked it. There are more articles on mathematics and music here: https://plus.maths.org/content/tags/mathematics-and-music