Guidance on Matching criminals
Assuming that the same number of people are born on every day of the year and that there are 365 days in a year, the probability of finding someone sharing your birthday is 1/365.
Now suppose you are interested in any two people in a group having matching birthdays. Let's first think about a group that has no matching birthdays. Then the first person in the group can have any of the 365 birthdays. The second person can have 364 out of the 365 birthdays in order to not match the first person. The third person can have 363 out of the 365 birthdays in order to not match either of the first two people, and so on. So that the probability that your group of size N (up to 365 people) has no matching birthdays is:
P(No matching birthdays) = (365/365) x (364/365) x (363/365) x ... x ( (365 - N + 1)/365).
Therefore, the probability that you have at least two people with the same birthday is:
P(At least one match) = 1 - P(No matching birthdays).
The following graph shows the probability of finding a matching pair of birthdays in a group of size N, plotted against N.
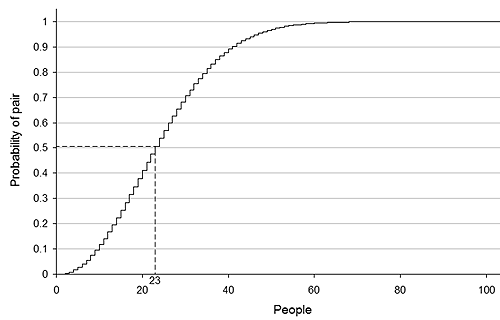
The probability of finding a matching pair of birthdays for number of people. Image from Wikipedia.
As shown in the figure, you need 23 people to have a 50:50 chance of two of them sharing a birthday. If you have 100 people, you can be 99.99997% sure that two of them will share a birthday. This result is known as the birthday paradox or birthday problem. It's called a "paradox" because intuitively you might guess that you'd need far more people, for example 365, to have a 50:50 chance that two share the same birthday.
What's the difference between looking for a person to match a given birthday and looking for two people sharing a birthday? In the first case, you're comparing everyone in a group of people to one other person, the one who's got the given birthday. In the second case, you compare everyone in a group to everyone else, so there are far more comparisons and therefore far more opportunities to find a match. For 23 people, looking for someone with a given birthday involves 23 comparisons, but looking for a matching pair involves 253 comparisons.
The birthday paradox helps explain the Arizona controversy. The chance of finding a DNA profile matching a given profile may be very small, but the chance of finding a matching pair of profiles is much larger. Therefore, the fact that the researcher found more matches than expected doesn't in itself prove that the DNA profiling technology is inaccurate.