Triples and quadruples: from Pythagoras to Fermat

Pythagoras' theorem. Image: Wapkaplet.

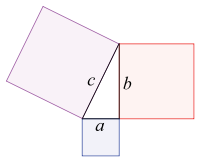
If there’s one bit of maths you remember from school it’s probably Pythagoras’ theorem. For a right-angled triangle with sides $a$ , $b$ , $c$ , where $c$ is the side opposite the right angle, we have

$a^2+b^2=c^2.$

If three positive whole numbers $a$ , $b$ and $c$ satisfy this equation — if they form the sides of a right-angled triangle — they are said to form a Pythagorean triple.

One question that intrigued Pythagoras himself, as well as other ancient Greek mathematicians, is how to generate Pythagorean triples. If I give you a positive number $a$ , can you find two numbers $b$ and $c$ so that $a$ , $b$ and $c$ form a Pythagorean triple? In this article we’ll explore this question, and we’ll also see how the idea extends to sets of four numbers, called Pythagorean quadruples.

Pythagorean triples

First of all, here are some examples of Pythagorean triples:

Some Pythagorean triples.

The triples written in red are multiples of each other and so are the triples written in blue: you get $(6, 8, 10),$ $(9,12,15)$ and $(12, 16, 20)$ by multiplying the components of $(3, 4, 5)$ by 2, 3 and 4 respectively, and you get $(10, 24, 26)$ by multiplying the components of $(5, 12, 13)$ by 2.

In general, if $k$ is a positive whole number and $(a,b,c)$ is a Pythagorean triple, then so is $(ka, kb, kc)$ , since

$(ka)^2+(kb)^2 = k^2a^2+k^2b^2 = k^2(a^2+b^2)=k^2c^2=(kc)^2.$

Geometrically, if one Pythagorean triple is a multiple of another, then the corresponding triangles are similar.

Pythagoras as depicted by Raffaello Sanzio in his painting The school of Athens.

If a Pythagorean triple isn’t a multiple of another Pythagorean triple, then we say that it is a primitive triple. You can recognise a primitive Pythagorean triple by the fact that the numbers $a$ and $b$ do not have a common divisor. In our example $(3, 4, 5)$ is a primitive Pythagorean triple while $(6, 8, 10),$ $(9, 12, 15)$ and $(12, 16, 20)$ are not. Similarly $(5, 12, 13)$ is a primitive triple whereas $(10, 24, 26)$ is not.

If you're given a Pythagorean triple it's easy to generate new non-primitive ones simply by taking its multiples. But given just a number, can you find a Pythagorean triple with that number as one of its components? One method for doing this has been attributed to Pythagoras himself. First note that if

$a^2+b^2=c^2$

then

$c^2-b^2=a^2.$

Now consider the two expressions

$(a^2+1)^2 = a^4+2a^2+1$

and

$(a^2-1)^2 = a^4-2a^2+1.$

They differ by exactly $4a^2,$ so the two expressions

$\frac{(a^2+1)^2}{4}$

and

$\frac{(a^2-1)^2}{4}$

differ by $a^2.$

Plato (left) with Aristotle (right) as depicted by Raffaello Sanzio in his painting The school of Athens.

Therefore, if we choose

$b=\sqrt{\frac{(a^2-1)^2}{4}}=\frac{(a^2-1)}{2}$

and

$c=\sqrt{\frac{(a^2+1)^2}{4}}=\frac{(a^2+1)}{2}$

we have

$a^2+b^2 = a^2 + \frac{(a^2-1)^2}{4} = \frac{(a^2+1)^2}{4} = c^2.$

For the numbers $a$ , $b$ and $c$ to represent a Pythagorean triple we need

$b =\frac{(a^2-1)}{2}$

and

$c = \frac{(a^2+1)}{2}$

to be whole numbers. This means that both

$a^2-1$

and

$a^2+1$

need to be even, which in turn implies that $a^2$ needs to be odd. But the square of a number is odd only if the number itself is odd, so this method only works for odd $a$ .

There is however an easy way to derive a formula for even values from the above. If $a$ , $b$ and $c$ form a Pythagorean triple of the form described above, then so do

$a_1=2a,$

$b_1=2b=a^2-1=\left(\frac{a_1}{2}\right)^2-1$

$c_1=2c=a^2+1=\left(\frac{a_1}{2}\right)^2+1.$

This method for generating triples from even numbers $a_1$ has been attributed to Plato. Here is a list of Pythagorean triples generated from both even and odd numbers using these two methods:

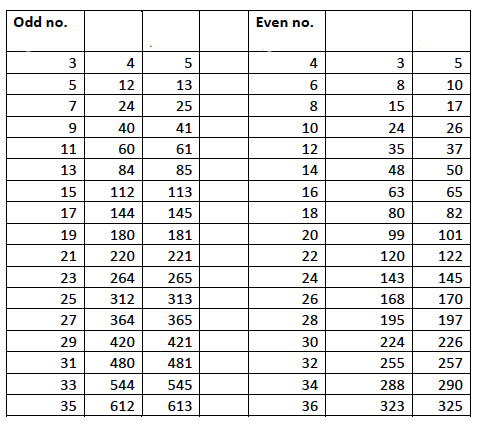
Since the methods give us a triple for every positive whole number we see that there are infinitely many Pythagorean triples. But can these methods generate all of them? The answer is no. For example, the triple $(20, 21, 29)$ is absent from the list above. A general formula was described by Euclid in his famous book The Elements. Take any two positive whole numbers $m$ and $n$ with $m>n$ . Similarly to our reasoning above, notice that

$(m^2-n^2)^2 = m^4-2m^2n^2 +n^4$

and

$(m^2+n^2)^2 = m^4+2m^2n^2 +n^4$

differ by $4m^2n^2.$ So setting

$a = m^2-n^2$

$b=\sqrt{4m^2n^2} = 2mn$

$c=m^2+n^2$

gives

$a^2+b^2=c^2.$

Since $m$ and $n$ are positive whole numbers and $m>n$ all three numbers $a$ , $b$ and $c$ are also positive whole numbers, so we have a Pythagorean triple. Every primitive Pythagorean triple can be generated from a unique pair of numbers $m$ and $n$ , one of which is even. And once you have the primitive ones you can generate all Pythagorean triples simply by multiplying. So Euclid’s formula really does give you all the triples there are.

Pythagorean quadruples

Now let’s look at Pythagorean quadruples which consist of four positive whole numbers instead of three. In a Pythagorean quadruple the sum of squares of first three numbers gives us the square of the fourth:

$a^2+b^2+c^2=d^2.$

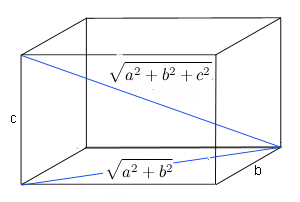
Geometrically we can think of a Pythagorean quadruples in terms of a rectangular box with sides $a$ , $b$ and $c$ . The length of the diagonal of this box is

$\sqrt{a^2+b^2+c^2}.$

Hence the sides together with the diagonal form a Pythagorean quadruple. This is why Pythagorean quadruples are also called Pythagorean boxes. As before, if $(a,b,c,d)$ is a Pythagorean quadruple, then so is $(ka,kb,kc,kd)$ for any positive whole number $k$ . If the greatest common divisor of $a$ , $b$ and $c$ is 1 then the quadruple is called primitive. Here are some examples of Pythagorean quadruples with members that are multiples of each other in the same colour (red, blue or green):

Some Pythagorean quadruples.

We can generate a Pythagorean quadruple from any two numbers $m$ and $n$ simply by noting that

$(m+n)^2=m^2+2mn+n^2.$

Thus, setting

$a = m^2, b = 2mn, c= n^2$ and $d=(m+n)^2$ gives us a Pythagorean quadruple.

This also gives us a way of generating a Pythagorean quadruple from a single even number $p$ . Firstly, note that if $p$ is even, then $p^2$ is even. Now find two numbers $m$ and $n$ so that $m n = p^2/2.$ Set

$a=m$

$b=p=\sqrt{2mn}$

$c=n$

and

$d=(m+n)^2.$

Then

$a^2+b^2+c^2 = m^2+ 2mn + n^2 = (m+n)^2 = d^2$

gives us our Pythagorean quadruple. For example, if $p=2$ , then $p^2/2=2$ so choose $m=1$ and $n=2.$ We get the quadruple $(1, 2, 2, 3)$ with

$1^2+2^2+2^2 = 1+4+4=9=3^2.$

For $p=4$ we have $p^2/2=8.$ We now have two choices as $8=2 \times 4$ and $8=1 \times 8.$ The first choice gives the quadruple $(2, 4, 4, 6)$ with

$2^2+4^2+4^2 = 4+16+16 = 36 = 6^2.$

The second choice gives the quadruple $(1, 4, 8, 9)$ with

$1^2 + 4^2+8^2 = 1 + 16 + 64 = 81 = 9^2.$

You can continue to generate quadruples from even numbers $p$ in this way.

Can we generate all Pythagorean quadruples?

Not all Pythagorean quadruples are of the form

$(m+n)^2=m^2+2mn+n^2,$

so not all of them can be generated using the method we just described — we need to be a little cleverer. Suppose that you’re given two numbers $a$ and $b.$ Now find a number $p$ which divides $a^2+b^2$ but so that $p^2 < a^2+b^2.$ If $a$ and $b$ are both even, then we also require that $p$ itself is even.

Euclid (the man with the compass) as depicted by Raffaello Sanzio in his painting The school of Athens.

Now let

$c= \frac{a^2+b^2-p^2}{2p}.$

Then

$\displaystyle a^2+b^2+c^2$	$\displaystyle =$	$\displaystyle a^2+b^2+\frac{(a^2+b^2)^2-2(a^2+b^2)p^2+p^4}{4p^2}$
$\displaystyle$	$\displaystyle =$	$\displaystyle a^2+b^2 +\frac{(a^2+b^2)^2}{4p^2}-\frac{(a^2+b^2)}{2}+\frac{p^2}{4}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{(a^2+b^2)^2}{4p^2}+\frac{(a^2+b^2)}{2}+\frac{p^2}{4}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left(\frac{(a^2+b^2+p^2)}{2p}\right)^2.$

So letting

$d = \frac{(a^2+b^2+p^2)}{2p}$

we have

$a^2+b^2+c^2=d^2.$

But are $a$ , $b$ , $c$ and $c$ positive whole numbers? This is why we’ve imposed conditions on $p.$ You can show that as long as $a$ and $b$ are either both even, or if one is even and one is odd, then the conditions ensure that $a$ , $b$ , $c$ and $d$ are positive whole numbers.

(Click here to see why.)

If $a$ and $b$ are both odd it is impossible to generate a Pythagorean quadruple from them by this method.

But the important point is that you can construct every primitive Pythagorean quadruple from two numbers $a$ and $b$ in the way we’ve just shown. And again, once you have the primitive ones, you can get all the others just by multiplying.

Generating a series of squares

Another nice thing to notice is that using our mechanism for generating triples, we can make sums of squares of any length. Let’s start with the triple $(3,4,5).$ We can generate another triple starting with the number 5: it’s $(5,12, 13).$ Thus we have

$3^2 + 4^2 = 5^2$

and

$5^2 + 12^2 = 13^2.$

Rearranging the second equation gives

$5^2 = 13^2-12^2.$

Substituting this into the first equation and rearranging gives

$3^2+4^2+12^2=13^2,$

so we have the quadruple $(3,4,12,13).$ Proceeding in a similar way, always using the biggest of the current set of numbers to generate a new triple, we can construct the quintuple $(3, 4, 12, 84, 85)$ and the sextuple $(3, 4, 12, 84, 3612, 3613)$ and so on, ad infinitum.

Cubes and beyond

Pythagorean quadruples consist of a sum of squares, but what if we look at sums of cubes of the form

$a^3+b^3+c^3=d^3.$

These are called cubic quadruples. Here are a few examples (again, quadruples written in red, blue or green are multiples of each other).

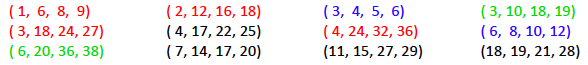
Some cubic quadruples.

We won’t explore how to generate them here, but instead ask a question that turns out to be more interesting: are there also cubic triples? This question is the subject of one of the most famous results in mathematics: Fermat’s last theorem. The theorem says that there are no three positive whole numbers $a$ , $b$ and $c$ such that

$a^3+b^3=c^3.$

In fact, the theorem says more than that: for any positive whole number $n$ greater than two it is impossible to find three positive whole numbers $a$ , $b$ and $c$ such that

$a^ n+b^ n=c^ n.$

The result was made famous by the French mathematician Pierre de Fermat in 1637. Fermat wrote in the margin of his book that he had "discovered a truly marvelous proof of this, which this margin is too narrow to contain". For over 300 years mathematicians desperately tried to reconstruct this marvellous proof, but they didn't succeed. It was not until 1995 that the mathematician Andrew Wiles proved the result, using sophisticated mathematics Fermat could not possibly have known about.

About the author

Chandrahas Halai is a mathematics enthusiast from the land of the Shulba sutras, the Bakhshali manuscript, and mathematicians like Aryabhatt, Brahmagupta, Bhaskaracharya, Ramanujan and many more. He is a consultant in the field of computer aided engineering, engineering optimisation, computer science and operations research. He writes research papers, articles and books on mathematics, physics, engineering, computer science and operations research. In his spare time he likes doing nature photography and painting.

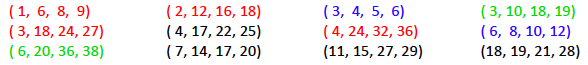
Comments

Very Interesting article

This is truly an interesting article and gives a newer insight to theorems that we have been using for years. The method shown to generate quadruple from triplets is mind-boggling. I am wondering about similar triplets and quadruples for non-integers. atul-Mumbai

Mr. Atul, Thank you for

Mr. Atul,
Thank you for liking the article. The article is on number theory, which deals with properties of integers.
As it is for real numbers you can have infinite solutions for triples and quadruples.

Pythagoras to Fermat by Chandrahas Halai

Quite interesting.. Chandrahas has a passion for mathematics.He attributes this to great teachers of his early years.Compliments to Chandrahas.......Prof.V.H. iyer, Ph.D., Dean, We School,Mumbai.

Thank you for the words of

Thank you for the words of encouragement, Sir!

Thanks

Thank you Chandrahas Halai for such a story.
Mohammad Abul Hosein
O-A Level Maths Teacher
Bangladesh
e-mail: ahossain69@yahoo.com

You are welcome, Sir! This is

You are welcome, Sir!
This is encouraging me to write more such articles.

Pythagorean Triples

Pythagorean triples can be easily identified by expressing the equation as (p+q)^2-(p-q)^2 = 4pq which clearly has an integer square root if both p and q have integer square roots.

Can you elaborate on

Can you elaborate on this?
And can you kindly introduce yourself.

Thanks, and a small error

Very belatedly catching up on Plus articles. I enjoy these articles - although as a Masters student the maths is familiar to me already, the authors are clearly very interested in their topics and that enthusiasm comes through! Thank-you for your enthusiasm.

In the section where Pythagorean quadruples are introduced, your geometrical explanation is slightly incorrect - the diagonal of the box is of course sqrt(a^2+b^2+c^2) and not simply a^2+b^2+c^2 as written. Similarly for the diagonal of the bottom face in the diagram.

Thank you for pointing the

Thank you for pointing the error! We've corrected it.

Nice article!

I very much enjoyed your article. I have an interest in Euler bricks which are related to your quadruples in that a "perfect" one (as yet undiscovered; perhaps impossible) would not only have an integer body diagonal, but all the face diagonals would be integers as well.

Enjoy thinking about it. OEIS Sequence A211133 is also related.

Best wishes, Alan

Typos

I am confused by:

Thus, setting $a = m^2, b = 2mn, c= n^2$ and $d=(m+n)^2$ gives us a Pythagorean quadruple.

I think it should actually be

Thus, setting $a^2 = m^2, b^2 = 2mn, c^2= n^2$ and $d^2=(m+n)^2$ gives us a Pythagorean quadruple.

It should be noted that $b^2= 2 m n$ does not give us an integer $b$ unless $2 m n$ is a perfect square. In the following set of equations $ d=m+n$ and not $d=(m+n)^2$.

The section on extending to longer sequences is very interesting.

I agree - quadruple generator has an error

I agree with Anonymous that the statement for generating Pythagorean quadruples is incorrect. Moreover, since the correct statement would require b^2 = 2mn, b would, in general, not be an integer. There is a correct formula at http://mathworld.wolfram.com/PythagoreanQuadruple.html.

pythagorean stuff

You can also take the values and put them in a column array, and multiply it by the same values in a row array. This is how we get our hyper sphere.

(9/13053769)^2+(12/13053769)^2+(36/13053769)^2+(252/13053769)^2+(10836/13053769)^2+(12/13053769)^2+(16/13053769)^2+(48/13053769)^2+(336/13053769)^2+(14448/13053769)^2+(36/13053769)^2+(48/13053769)^2+(144/13053769)^2+(1008/13053769)^2+(43344/13053769)^2+(252/13053769)^2+(336/13053769)^2+(1008/13053769)^2+(7056/13053769)^2+(303408/13053769)^2+(10836/13053769)^2+(14448/13053769)^2+(43344/13053769)^2+(303408/13053769)^2+(13046544/13053769)^2=1

I would like to complement

I would like to complement you on a well written article but alas mathematically, for me at least it lacks coherency and substance. It takes one slowly through some seemingly simple yet carefully selected equations allowing triples to be generated from (1) odd numbers (2) even numbers and then gives a table with examples of both.
As the given equations do not generate all triples we are then presented with the formulas for Euclid's numbers given in The Elements (which book, which proposition because I can't find it!) but nowhere is there an example of these coherently structured numbers. Also Euclid's numbers combine to give a three term equation which is just the 'Quarter Squares Rule', The Elements, book 2, proposition 8 and which was posted in a comment by anonymous on 20/12/2012.
Incidentally, about the author says that you are from the land of Aryabhatt the Elder who way back in the 5th century knew that the partial sums of the cubes, 1^3 + ... +n^3 = a triangular number squared and from which one can easily derive the 'Quarter Squares Rule'.
Apart from a hint at their existence you do not raise the question of infinite odd and even series of Pythagorean triples which is essential if one is to make sense of a table of 10,000 triples which one can download from the internet. After I managed to sort series out to my satisfaction I programmed Excel to generate any series of triples from just two number inputs which at the start of your article was the purported aim of the ancients.
And what about simply getting ones hands dirty and saying c^2 - b^2 = integer = a^2 IF and ONLY IF the integer equals a perfect square particularly in these days of computer spreadsheets.
Finally, what's the connection if any between Pythagorean triples together with quadruples and' Fermat's Last Theorem'.

But what if the inputs into

But what if the inputs into (a+b)² are themselves squares or more precisely pythagorean triples a²+b²=c². Then you will find we generate 3 related pythagorean quadruples, 2 with all 4 terms positive and the other with 3 positive and 1 negative term. (This later quadruple is WRONGLY NOT classified as a pythagorean quadruple by mathematicians). So for 3²+4²=5² we get: (i) 25² =20²+12²+9² : (ii) 25² =16²+15²+12² (iii) 20² =16²+15²-9² and this applies to every single pythagorean triple.
The Fermat triple is easily shown to algebraically generate the 3 self same quadruples but with the exponent 2 replaced by n but it should be observed that 2 terms in each quadruple are perfect squares since (aⁿ)(aⁿ)=a²ⁿ=(aⁿ)² and therefore all 3 quadruples can be stated as the difference of 2 squares. Someone on U-Tube has named them Fermat - Bateman quadruples. Furthermore every square integer and therefore every (aⁿ)² can be expressed as a NEGATIVE pythagorean quadruple whose terms are simple to derive so for example: 20² =16²+13²-5². Taking D² =C²+B²-A² then D-C=4 : B-A=8 : B+A= (D+C)/2. For D odd then B & A are rational with a decimal fraction of 0.5.
Also every integer of the form (4n)² is the sum of 4 adjacent odd integers squared minus 20=4²+2² hence 20² =13²+11²+9²+7²-20 and which includes every (4nⁿ)². Note that the sum of the 2 largest terms which for the example is 13+11=24 and is always 4 more than the total sum. So every term of a Fermat triple if one existed would have a simple solution in terms of squares after squaring once or infinitely many times so as Pierre de Fermat said 350 years ago triples above the second power cannot exist. So for it to be repeatedly stated and dogmatically defended that the tools for him to have proved his theorem did not exist in his day is at the least erroneous and at worst a lie. It is for the reasons given that no quadruples above the 4th power are known simply because they do not and cannot exist. It is worth stating that cubic quadruples also contain infinitely many related trios but none are algebraically of the construction of Fermat-Bateman quadruples. For example: 12³=10³+9³-1³ : 9³=8³+6³+1³ : 12³-10³=9³-1³=8³+6³ therefore 12³=10³+8³+6³ divide by 2³ gives 6³=5³+4³+3³ the smallest all integer cubic quadruple.

An algorithm to find all Pythagorean Triples

The following algorithm may be used to find ALL Pythagorean Triples. And you find ONLY Pythagorean Triples. No need to check for correctness.
- Start with an even square number (4,16,36,64,100 etc.).
- Divide it by 2 you get (2,8,18,32,50 etc.)
In the continued description, I use 36 (6^^2) as example
- Factorize it in pairs included the factorization where 1 is one of the factors you get the following pairs:
(1,18), (2,9), (3,6)
Each pair will generate a Pythagorean triple as follows) (example using (1,18)):
a= 1+6 (the originating number squared)
b=18+6
c=1+18+6
giving the triple (7,24,25)

How to find this algorithm, see link
http://fermatslibrary.com/p/56b57e1c

BTW, this is probably Fermat's own first step on how he proved his last theorem.

Illuminating

What a brilliant articles...very illuminating, right upto Format's theorem.

Plus.Maths.org