
There are a lot of everyday situations where people make decisions one after the other, and what is decided earlier affects the choices later on. One of the more serious of these is finding a partner. Most people want to find the best possible partner.

Generally in Britain, you only have one partner at a time. Typical human behaviour is to have a succession of friendships, which come to an end when you decide that the current friend is not suitable to be your partner, and eventually you find "Mr Right" or "Miss Right" and then you make the decision not to go on looking any more. Quite often, social etiquette means that you can't go back to one of the people that you have rejected earlier, and you can't find out much about anyone who might come along later.
At the British Psychological Society's conference in April 1997, on Dr Peter Todd, of the Max Planck Institute in Munich, spoke about the best (optimal) strategy for finding a partner. He also drew a parallel with the employer trying to find a suitable new employee from a range of applicants, and quoted the 37% rule. Once you have seen 37% of the application forms, "a coherent picture of the ideal employee is built up and the next person to fulfil these criteria gets the job".

Psychologists in several universities have been looking at the way that human beings, animals and birds behave when searching for a mate. For some reason, the mating behaviour of pied flycatchers has been extensively studied over the last decade. A rule which determines the best strategy to follow was developed in the middle of the 1960's, and some birds do follow this quite closely in practice.

It is possible to simulate the process of making decisions one after another. "Googol" is a game which was described by Martin Gardner in his column in the "Scientific American". Scattered over a table, there are a lot of cards, face down. Each one has a sum of money written on the hidden side, and you are allowed to look at one card at a time, decide whether to take the money or throw the card away. What should you do?
Other university researchers have looked at the way people go house-hunting. Looking for an ideal place to live is a problem which has many similar features to that of choosing a partner, although it is a little easier to change a house than to change a partner!

How does a mathematician look at such problems? In each case, you have to make decisions in succession. Each time you make a decision, you either stop and have a reward, or you take the risk of going on to another decision, choosing a partner, a sum of money, a house, an employee. This mathematical approach is called "optimal stopping".
Optimal Stopping
Like all mathematical models, we need some assumptions. The model simplifies the real world, and we need to agree on the way that we build the model.
Here, we will assume that if you looked at all the potential partners (or sums of money), you could put them into order without making any two equal. But if you can't look at all of the partners, you must be able to work out the order for those that you have seen, and be able to tell if you meet someone who is better than any of them. We will assume that there are N potential partners, who could be ranked 1 (the worst) to N (the best). We assume that you meet them in a random order. If there were 4, each of the 24 orders below would have the same chance of occurring.
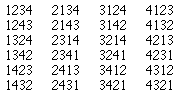
What do you want to achieve? In the language of mathematics, what is your objective function? The simplest model for this problem is to try to make the chance of finding the best partner as large as possible.
It turns out that the best way of selecting is to look at M-1 of the potential partners (where M ranges from 1 to N) and then choose the first one who comes along afterwards who is better than the best that you have seen among those M-1. The reason that this is best is because when you have seen, say 2 potential partners, with one better than the other, you still don't know whether these are the two best or the two worst or anywhere in between. So you want to use the information that you have before it is too late!
(The reason for doing the calculations with M-1 is that M is the Minimum number of potential partners that you will encounter; there are M-1 who give you the data you need before you start searching, and the Mth who is the first who can be accepted.)
When N is 4, you can make a table of the times when you would win with each value of M.
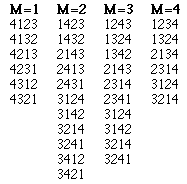
The best value of M is 2, when you find the best partner on 11 occasions out of the possible 24. Choosing the first or the last potential partner means that you find the best one on 6 occasions, which is the same as picking randomly, 1 in N.
But what happens for bigger N?
You can follow the same exhaustive rule when N is 5 (120 possibilities) and 6 (720 possible orders for meeting partners) but for bigger values, it is sensible to try and find a simpler (less time-consuming) way of finding the answer. It turns out that there is a simple relationship between the best value for M given N potential partners when N is large: the 37% rule. This relationship is derived in a separate article in this issue. See "Optimal stopping".
Mathematics of finding a partner and eating out
Building models like this gives interesting results, but you don't know, at the age of zero, how many potential partners you are likely to meet in your lifetime. Dr Peter Todd turned the problem around. Instead of trying to estimate the number of potential partners one could consider, he put forward a rule which would work for most people. He suggested that a typical person should count up to about a dozen potential partners, and then start hunting seriously. The first dozen would give enough information for a reasonable choice.
The same idea can be applied to the problem of trying to find somewhere to eat. Because of the limited time available before you get so hungry that you could eat anything, you estimate that you are likely to drive past 7 or 8 pubs, cafes and restaurants. The optimal policy then is to look at 2 or 3 of them before selecting. Hopefully you will be satisfied!
The author
Dr David K. Smith, Mathematical Statistics and Operational Research Department, University of Exeter
You can contact him via email D.K.Smith@exeter.ac.uk
David Smith studied mathematics before he went on to specialise in operational research. When The Independent reported on the British Psychological Society's conference in April 1997, see "Choosing a partner is like finding a job", he was prompted to write to the editor, see "Choice numbers", to point out that the Dr Todd's results were familiar ones, at least as far as the newspaper reported them. He was asked to expand on his letter for PASS Maths.