
Nowadays we take it for granted that someone in England can make a phone call to Australia, or that someone in India can read web pages that are on a computer in Canada. We live in a society in which almost every home has its own telephone line which is connected to a local exchange in the nearest village or town, from there to a main exchange in the nearest city, and from there to any other city in any country in the world. In this way, a person is able to dial a friend in another country just as easily as if they were in the same street.

Inside BT's Worldwide Network Management Centre at Oswestry.
(© British Telecommunications plc)
In order that these large and complicated networks can work properly, mathematics and computer simulation have to be used to understand the networks. The aim is to find out how large networks can be designed and controlled to provide reliable communications systems and to use resources efficiently. The reliable and efficient operation of networks is of vital commercial importance to both users and telephone companies, and even modest percentage improvements can correspond to large revenue gains.

BT cable laying in the City of London.
(© British Telecommunications plc)
A large network is affected by many factors which are often hard to predict. There can be busy and quiet periods through the day. If a television program has a phone-in vote, there can be a sudden overload at one point in the network. If a digger cuts through a major telephone wire while repairing the road, there can be a sudden and unexpected failure. Mathematicians have developed ingenious ways of routing calls which can cope with these unpredictable events. These routing schemes work by searching out the spare capacity in the network so as to route calls away from parts of the network that are broken or full and into parts that are underloaded.
A good routing strategy doesn't only need to be able to find the spare capacity in the network. In order to work well in real networks, it needs to be simple, so that thousands of calls a second can be routed instantly. It also needs to be decentralised; a central controller would be much too slow and could go disastrously wrong if it had a power failure, or got cut off from the rest of the network. Mathematicians have recently been able to show the surprising fact that these different goals can all be achieved simultaneously. Even simple, decentralised schemes can find the spare capacity as efficiently as more complicated schemes.
Erlang's formula

The chances of getting an engaged tone depends
on the number of lines out of the village.
The Danish mathematician A. K. Erlang was the first to study the problem of telephone networks. In 1917, he looked at a village telephone exchange. He supposed that the village has a certain number of telephone lines going from it to the outside world.
We'll call the number of lines C. People in the village want to make calls to the outside world. We don't know when they will want to call or how long their calls will last, but let's suppose that there are on average v calls starting per minute, and that the average length of a call is one minute. Erlang wanted to know what fraction of callers would find that all the C lines leading out of the village were already full, and so would not be able to make their call until later. He worked out this formula, which gives the answer:
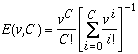
This is called Erlang's formula. The left hand side, E(v,C), represents the proportion of callers that find all the lines already full, and the right hand side gives an equation for that quantity. If you know how big v and C are, you can work out what proportion of calls cannot get out of the village.
Questions:
- Without calculating the formula, if C increased, would you expect E(v,C) to increase or decrease?
- If v increased, would you expect E(v,C) to increase or decrease?
If you were to try some different values for the forumula, you would find that when v and C are both doubled, E(v,C) decreases. This shows the surprising fact that using one large link is better than using two links half the size.
Erlang's model is a very simple one, but the mathematics underlying today's complex networks is still based on his work.
Trunk reservation
When we try and route calls through a whole network instead of just out of a single village, many surprising things can go wrong. For example, if a call from Aybury to Beeford finds that the direct link between them is full, it is tempting to route it via some other city, say Ceeville, if possible. This is a good thing to do if the network is lightly loaded, but if it is heavily loaded then most calls have to use an indirect route instead of a direct one, thus using two links instead of one. Because each call is using twice as many links as it needs, the network can then only carry half as many calls in total!
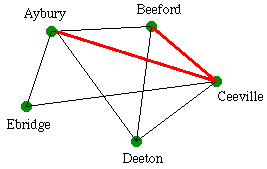
Network map showing calls from Aybury to Beeford being routed through Ceeville.
Mathematicians have devised a scheme known as trunk reservation to avoid this problem. We reserve some capacity on each link for directly routed calls. So if a link is becoming full, no indirect calls are accepted on it. The amount of reserved capacity only needs to be very small - maybe space for half a dozen calls on a link that could carry several hundred. This is a very simple scheme, and easy to implement in real networks.
The effect of trunk reservation is that we sometimes refuse to carry calls that we could fit in. It seems like this would be a bad thing to do. But in fact, by throwing away a few harmful calls, we can carry far more calls overall.
Sticky routing
Sticky routing is a principle that has been much studied in the last 10 years. Suppose that a call is to be connected between city A and city B but that all the direct links are currently busy. The routing strategy needs to find a longer path to get from A to B which can carry the call.To do this, city A remembers an intermediate city, C say, to use for such overflow calls and attempts to set up the connection from city A to city B via city C. If this connection is accepted then that two-link route is used for this call and is remembered for future calls between cities A and B.
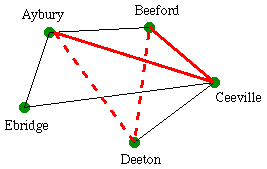
Network map showing change in route from Ceeville to Deeton.
If the two-link connection A-C-B is rejected because it is currently too busy then this call is refused connection (the person calling hears a engaged tone) and the intermediate city is reset at random to another city, D say. The next overflow call between cities A and B will then attempt to use the new path A-D-B.

Modern exchanges route large numbers of calls.
The sticky principle sticks to the same two-link route as long as it is not too congested, and then switches to a new path when congestion is seen. In this way, a sticky routing strategy searches for and uses any available spare capacity that exists in the network.
Summary

A computer controlled exchange.
In this article, we have looked at just a few of the ways in which mathematics has helped to solve difficult problems in large, complex communication networks. In 1996, the British Telecom network, which is based on main exchanges in about 60 cities, implemented a routing scheme called Dynamic Alternative Routing (DAR), which combines the ideas of trunk reservation and sticky routing. Mathematicians have shown that although this scheme uses very simple ideas, it performs almost as well as any scheme at all could possibly perform. This involved proving that there is an upper limit to the performance of any scheme.
As the technology improves, and new services such as "video on demand" become available, we can expect more challenges for mathematicians in the years ahead.
Further Reading
For further introductory articles on this subject see:
- "Simple is the Best for Dynamic Routing of Telecommunications" by Alistair Mees. Nature, volume 323, page 108, 11th September 1986.
- "Secrets of Network Success" by Nigel Bean. Physics World, volume 9, number 2, pages 30-33, February 1996.
- "Modelling Communication Networks, Present and Future" by Frank Kelly. Clifford Paterson lecture, in Philosophical Transactions of the Royal Society of London, Series A, volume 354, number 1707, pages 437-463, 1996.
The mathematics used in this area is covered in Probability courses at school, and in courses on Probability, Optimisation, Stochastic Processes and Markov Chains at university. Similar problems using the same sorts of mathematics also occur in computer networks, road networks, and in scheduling jobs in factories.
Acknowledgements
DAR was developed as a collaborative project involving researchers from the University of Cambridge Statistical Laboratory, led by Frank Kelly, and British Telecom Laboratories, led by Dave Songhurst.
Dr Richard Gibbens & Dr Stephen Turner, University of Cambridge Statistical Laboratory.
Answers to Erlang formula:
- If C increases, that means that more lines are built out of the village. So E(v,C), the proportion of calls that find all the lines already full, decreases.
- If v increases, that means that more calls are being made. So the proportion that find all the lines already full increases.