
I think it is still safe to say that most people have heard of Nick Leeson. In early 1995, Nick Leeson earned global notoriety when it was discovered that he had lost around $1.3 billion trading derivatives, bringing about the collapse of Barings Bank, one of the world's largest at the time. Nick was sentenced to six and a half years in jail. On his release he became the darling of the chat shows and his story has since been glamorised in a film.
The result of all this was to catapult the world of derivatives into the public eye. These financial instruments have since been viewed by the public as risky, dangerous bets akin to putting your house on the 4 o'clock at Newmarket. There is an element of truth in this, but as I hope to demonstrate, this is only half the story.
So what is a derivative?

Put simply, a derivative is a financial instrument whose value depends on the values of underlying variables. The underlying can be almost anything from the price of gold to the amount of snow falling in certain ski resorts (weather derivatives!). More commonly though, the underlying is the price of a traded asset, such as a share or a currency rate.
Forward (futures) contracts
The simplest type of derivative is a forward contract. This is an agreement to buy or sell an asset at a certain time in the future for a certain price. In entering into a forward transaction, one party agrees to buy a certain asset for a fixed price at a fixed date in the future, and the party on the other side of the transaction agrees to sell the asset on the same date for the same price.
The price that the underlying asset is bought / sold for is the delivery price. This price is chosen so that the value of the contract to both sides is zero at outset. What this means will be made clearer shortly - roughly it is that the price is fair, so neither party is ripping the other off.

The payoff from the forward is based on the actual price of the underlying asset on the delivery date. For example, let's assume that I enter into a forward transaction in which I agree to sell 100 pigs at £300 per pig in a year's time. (We're also assuming I don't have any pigs.) If the price of a pig is £350 at the end of the year, I make a loss on the forward transaction because I must buy 100 pigs at £350 each in order to meet my obligation to deliver the pigs. On delivery I only receive £300 per pig, a total loss of £5,000 (100 x (£350 - £300)) plus delivery costs. On the other hand if the price of pigs has plummeted to £250 each, I profit to the tune of £5,000.
In general, if K is the delivery price and S is the current price of the pig at time of delivery (or any underlying asset for that matter) the payoff will be
K - S
per pig (or unit) if I have agreed to sell pigs at a fixed price (known as a short position in pigs), and similarly
S - K
per pig if I have agreed to buy the pigs at a fixed price (known as a long position in pigs). These payoffs are illustrated in Figure 1 below.
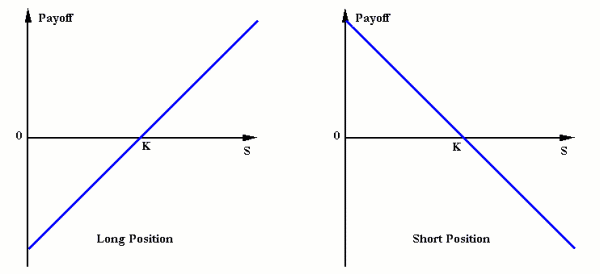
Figure 1. Payoffs from forward contracts
How do we determine the delivery price? Let's assume that cash can be deposited or borrowed at 5% per annum. If the current price of a pig is £300 and the forward price of a pig is £330 we can do the following:
- Borrow £300 at 5% interest for one year
- Buy a pig
- Enter into a short forward contract to sell a pig for £330 in one year's time.
- At the end of the year we sell the pig for £330, and repay the borrowing of £300 plus £15 interest.
We have made a risk free profit of £15. In fact any delivery price above £315 will result in a profit using this strategy. Likewise if the delivery price is below £315 we can do the following:
- Sell a pig for £300 (assuming we have one!)
- Deposit £300 at 5% interest for one year
- Enter into a long forward contract to repurchase the pig in one year's time for the delivery price.
- At the end of the year we buy back the pig at the delivery price.
As long as the delivery price is under £315 a risk free profit emerges. In theory investors in the pig market will try to take advantage of any forward price that is not equal to £315. These trading activities (known as "arbitrage") will result in the forward price being exactly £315. This is known as an arbitrage free price as any other price results in an arbitrage opportunity.
What does all this tell us? First the forward transaction costs nothing for either party to enter into. (The arguments above showed that either party could safely agree to the transaction without making a loss by suitable borrowing / lending, etc.) Second the total return between the two parties will be the interest that can be earned on cash (£15 in the example above); however the payoff for one party is the opposite to that of the other, that is, for every winner there is a loser. This illustrates the speculative nature of some of these instruments when traded in isolation and the reason that Nick Leeson came a cropper. When forward contracts are traded on their own for speculative purposes, they can indeed be equivalent to betting on a racehorse. (In fact speculative trading in options, which are discussed below, is far more dangerous than the kind of forward transaction we've considered here.)
Although this illustrates the potentially speculative nature of forward transactions and the dangers of being able to enter into a large number of contracts at zero cost, there are a variety of ways in which these contracts can be used to reduce risk. This is known as hedging.
Extending the pig example, say a pig farmer has a good year in which his pigs sire 100 piglets. The current price is £300 and the farmer is concerned that this may fall or at least not grow in line with the one-year forward price of £315. He would be happy to receive £31,500 for his pigs in a year's time. The farmer sells 100 forward contracts on his pigs. He will then sell his 100 pigs (once they have grown up) for the fixed amount of £31,500 in a year's time. This allows him to prevent a reduction in value due to the price of pigs falling as well as enabling him to fix his future cashflows to reduce the uncertainty of his business. The farmer has hedged his exposure to pig prices - he has hedged his bets.
One of the most common uses of forward contracts is to hedge currency movements. For example, a company may be aware that they will receive a $1 million payment in a month's time. If they don't want to be exposed to movements in the sterling dollar exchange rate over the month they can sell 1 million dollars of a one-month forward contract on the sterling dollar exchange rate. If the one-month exchange rate is 0.6 pounds per dollar then the company can agree to sell the payment forward for £0.6 million and remove their dollar exposure.
Options
A more interesting type of derivative is an option. In this type of contract one of the parties has the option to buy or sell an underlying asset for a fixed price at a fixed time in the future. There are two basic types of option.
A call option gives the holder the right, but not the obligation, to buy the underlying asset at a certain price (the strike price) on a certain date.
A put option gives the holder the right, but not the obligation, to sell the underlying asset at a certain price on a certain date.
The fact that the holder has the option to exercise rather than the obligation leads to the one-sidedness of the instrument, which is illustrated in the figures that follow.
Suppose I buy a call option on BP, giving me the option to buy 100 shares in 3 months time for £6.00, and the current price is £6.00. If after 3 months the share price is below £6.00 there is obviously no point in exercising the option. In order to exercise the option I would have to purchase the shares at £6.00 and only be able to sell them for less. If the share price is above £6.00, however, the option will be exercised. For example, if the share price were £6.50 I would exercise the option, buy the 100 shares for £6.00 a share and sell them for £6.50 a share. This would net a profit of £50, minus the price I paid for the option.
Options cost money, the premium, and so it is useful to look at a profit profile rather than a simple payoff profile.
Figure 2 shows the profit profile for a purchased call option. This illustrates the fact that the maximum loss when buying these instruments is the original premium paid. The profit is:
max (S - X, 0) - C
where S is the price of the underlying share at the time of exercise, X is the strike price and C the call option premium. Note that when S is less than X I would not exercise the option (I wouldn't buy the shares at the strike price) so no further loss is incurred.
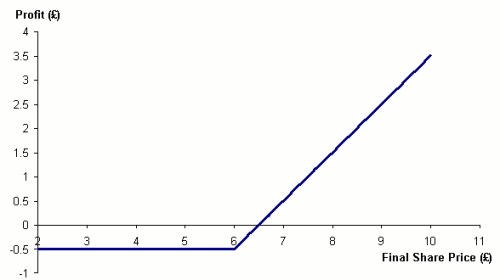
Figure 2. Profit from bought call option: option price £0.50, strike price £6.00
Similarly suppose I purchase a put option on BP giving me the option to sell 100 shares in 3 months time for £6.00. The cost may be £0.30. In this case the option will only be exercised if the share price falls, in which case I can buy the shares on the market for the reduced price and sell them through the put option at £6.00. Figure 3 shows the profit profile for the put option, which is defined as follows:
max (X - S, 0) - P
where P is the price of the put option. In this case, when S is greater than X the option would not be exercised and again the loss is limited to the original premium.
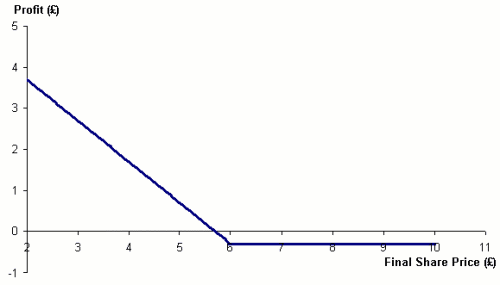
Figure 3. Profit from bought put option: option price £0.30, strike price £6.00
In both cases above the graphs represent the situation from the option purchaser's point of view. In each case the maximum loss is the option premium. There are two sides to every option contract though; on the other side is a party who has sold (or written) the option. The writer of the option receives the premium up front but has potential liabilities later. The profit profiles are the exact opposite of those above (Figures 4 and 5).
Sold Call Option: C - max (S - X, 0)
Sold Put Option: P - max (X - S, 0)
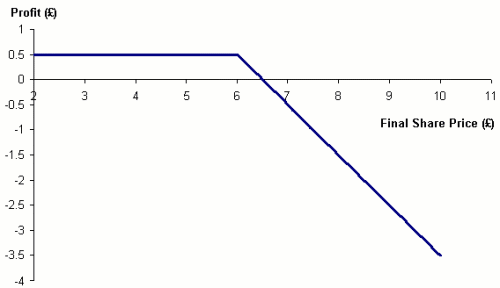
Figure 4. Profit from sold call option: option price £0.50, strike price £6.00
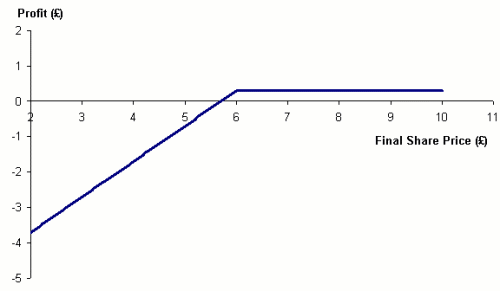
Figure 5. Profit from sold put option: option price £0.30, strike price £6.00
In these cases, there is only a small potential profit with extremely large, even unlimited, potential losses. Buying and selling options in isolation is a risky business (similar to forward transactions); in particular, writing options can be very speculative due to the potentially unlimited nature of the loss.
So much for the risky stuff. What about hedging with options? If I own 100 BP shares they are currently worth £600. I hope that they will go up in value but I also worry that they will fall drastically. I can buy a put option with a strike price of £6.00 allowing me to sell 100 shares in three months time. For the price of the put option (£30 in my example) I can 'insure' against falls in the share price, but still offer the potential for profit from good performance.
Figure 6 illustrates the point. The combination of shares and option will put a floor on my portfolio value of £570. This is a little like insurance in concept: I pay a small premium to someone who will cover any large losses should they occur. The premium will represent the expected value of these losses plus a small profit.
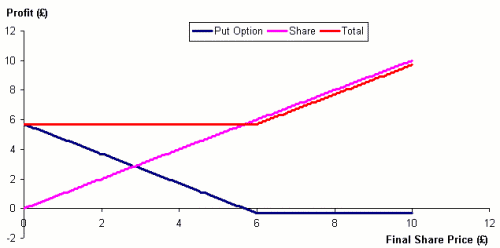
Figure 6. Hedging of Downside Risk
I may feel that £30 is a lot to pay to give me this level of protection and that actually I am prepared to take some risk in my investments. I could for instance buy a put option with a strike price of £5.00 and accept a maximum loss of £100 (plus the price of the put option). This may reduce the cost of the put option to £0.05 per share or £5.
This is a powerful yet simple hedging strategy used extensively by companies in the UK to insure against large losses on their balance sheets.
Exotic options
There is an almost unlimited variation in the types of derivatives available. Many of these are innovations in the underlying asset or variable.
Credit derivatives depend on the credit worthiness of a company.

Weather derivatives have payoffs depending on the average temperature at particular locations. Ski resorts may use them to protect against high temperatures affecting income because of lack of snow.
Insurance derivatives have payoffs dependent on the amount of insurance claims. A general insurance company might use them as protection against catastrophic claims due to storms.
Electricity derivatives have payoffs dependent on the price of electricity. These might be used by companies who use a lot of electricity in order to protect profits from extreme movements in electricity prices.
Often there are innovations in the measurement of the price of the underlying asset on exercise, such as the average over the last month or the lowest or highest level over the last month.
Alternatively the payoff profiles can be made extremely complicated - although these are usually based on combinations of the basic building blocks of forwards and options.
And finally ...
Derivatives can be risky when used in isolation to speculate on the performance of underlying assets in the future. Equally, though, derivatives offer a flexible and efficient method of reducing risk when used in connection with the underlying assets. Effectively, they can be used as insurance against losses.
About the author
John Dickson is a Fellow of the Faculty of Actuaries. He is currently working at Abbey National Asset Managers in the Investment Division, for companies such as Scottish Mutual and Abbey National Life, where he is responsible for all investments in long term structured assets (including derivatives). Their use of such derivatives is primarily for the purposes of reducing risk and for capital management of their life companies.