Add new comment

An infinite series of surprises

Mar 2002

Introduction

An infinite sum of the form

$\begin{equation} a_1 + a_2 + a_3 + \cdots = \sum _{k=1}^\infty a_ k, \end{equation}$

(1)

is known as an infinite series. Such series appear in many areas of modern mathematics. Much of this topic was developed during the seventeenth century. Leonhard Euler continued this study and in the process solved many important problems. In this article we will explain Euler’s argument involving one of the most surprising series.

You are likely to have already met perhaps the most important series which is the geometric progression. Given constants $a$ and $r$ we want to sum

$\begin{equation} a + ar + ar^2 + \cdots + ar^ N. \end{equation}$

(2)

If $|r|<1$ we can make sense of the infinite sum – something known by Newton – which is

$\begin{equation} \label{eq:gp} a + ar + ar^2 + \cdots + ar^ N + \cdots = \frac{a}{1-r}. \end{equation}$

(3)

This was one of the first, and only, general results known during the seventeenth century. Another series then known was

$\displaystyle \sum _{k=1}^\infty \frac{2}{k(k+1)}$	$\displaystyle =$	$\displaystyle 1 + \frac{1}{3} + \frac{1}{6} + \frac{1}{10 }+ \frac{1}{15} + \cdots$	(4)
$\displaystyle$	$\displaystyle =$	$\displaystyle 2 \left[ \frac{1}{2} + \frac{1}{6} + \frac{1}{12}+ \frac{1}{20} + \cdots \right]$	(5)
$\displaystyle$	$\displaystyle =$	$\displaystyle 2 \left[ \left( 1 - \frac{1}{2}\right) + \left( \frac{1}{2} - \frac{1}{3}\right) + \left( \frac{1}{3} - \frac{1}{4}\right) + \left( \frac{1}{4} - \frac{1}{5}\right) + \cdots \right]$	(6)
$\displaystyle$	$\displaystyle =$	$\displaystyle 2 \label{eq:Bernoulli}.$	(7)

Similar methods were used to find the sums

$\begin{equation} \sum _{k=1}^\infty \frac{k^2}{2^ k} = 6 \quad \mbox{and}\quad \sum _{k=1}^\infty \frac{k^3}{2^ k} = 26. \end{equation}$

(8)

Now all these series converge. That is to say we can make sense of the infinite sum as a finite number. This is not true of a particularly famous series which is known as the harmonic series:

$\begin{equation} 1 +\frac{1}{2} +\frac{1}{3} +\frac{1}{4} + \cdots = \sum _{k=1}^\infty \frac{1}{k}. \end{equation}$

(9)

The following medieval proof that the harmonic series diverges was discovered and published by a French monk called Orseme around 1350 and relies on grouping the terms in the series as follows:

$\displaystyle$	$\displaystyle$	$\displaystyle 1 +\frac{1}{2} +\frac{1}{3} +\frac{1}{4} +\frac{1}{5} +\frac{1}{6} +\frac{1}{7} + \cdots$	(10)
$\displaystyle$	$\displaystyle =$	$\displaystyle 1 +\frac{1}{2} + \left(\frac{1}{3} +\frac{1}{4}\right) + \left(\frac{1}{5} +\frac{1}{6} +\frac{1}{7} +\frac{1}{8}\right) +\left( \frac{1}{9} +\frac{1}{10} +\frac{1}{11} +\frac{1}{12} +\frac{1}{13} +\frac{1}{14} +\frac{1}{15} +\frac{1}{16}\right) + \cdots$	(11)
$\displaystyle$	$\displaystyle \geq$	$\displaystyle 1 +\frac{1}{2} +\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+ \cdots$	(12)

The harmonic series diverges

It follows that the sum can be made as large as we please by taking enough terms. In fact this series diverges quite slowly. A more accurate estimate of the speed of divergence can be made using the following more modern proof. This uses a technique known as the integral test which compares the graph of a function with the terms of the series. By integrating the function using calculus we can compare the sum of the series with the integral of the function and draw conclusions from this.

In this case we compare terms in the series with the area under the graph of the function $1/(1+x)$ . In particular, figure 1 shows that

$\begin{equation} \sum _{k=1}^ n\frac{1}{k} >\int _0^ n \frac{1}{1+x}\mathrm{d}x. \end{equation}$

(13)

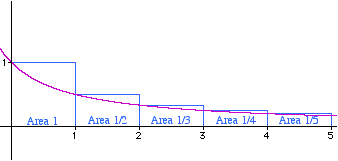
Figure 1: The series 1/n above the graph of 1/(1+x)

Of course the integral on the right is easy. Solving this gives

$\begin{equation} \sum _{k=1}^ n\frac{1}{k} > \ln (1+n). \end{equation}$

(14)

Now, the function $\ln (1+n)$ is unbounded. By this we mean that there is no limit to how big we can make it by taking sufficiently large values of $n$ . So we can make $\sum _{k=1}^ n\frac{1}{k}$ as large as we please. A similar argument comparing the series to the function $1/x$ shows that

$\begin{equation} 1+ \ln (n)> \sum _{k=1}^ n\frac{1}{k} > \ln (1+n) \end{equation}$

(15)

so that we can estimate how fast the series diverges.

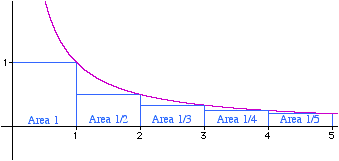
Figure 2: The series 1/n below the graph of 1/x

The harmonic series generalised

The harmonic series can be described as "the sum of the reciprocals of the natural numbers". Another series that presents itself as being similar is the "the sum of the squares of reciprocals of the natural numbers". That is to say, the series

$\begin{equation} \label{eq:basel} 1 +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} + \cdots = \sum _{k=1}^\infty \frac{1}{k^2}. \end{equation}$

(16)

The first question we ask is "Does this series converge?". If it does we next ask "What is the sum?". To answer the first question we notice that

$\begin{equation} 2k^2 \geq k(k+1), \end{equation}$

(17)

and so

$\begin{equation} \frac{1}{k^2} \leq \frac{2}{k(k+1)}, \end{equation}$

(18)

and comparing with terms in the series (4) that we encountered earlier gives that

$\begin{equation} \sum _{k=1}^\infty \frac{1}{k^2} \leq \sum _{k=1}^\infty \frac{2}{k(k+1)} = 2. \end{equation}$

(19)

Leibniz - image by permission of Gregory Brown (gbrown@uh.edu).

Bust of Leibniz by Johann Gottfried Schmidt

The series converges, but the exact value of the sum proves hard to find. Jakob Bernoulli considered it and failed to find it. So did Mengoli and Leibniz. Finding the sum became known as the Basel Problem and we concentrate on Euler's solution for the rest of this article.

"Infinite polynomial" - power series

Before solving this problem we look briefly at a piece of theory Euler used which allowed him to write the function $\sin (x)$ in a particular way. This really could (or perhaps should) be the subject of an article in its own right. What Euler knew, as as we will see in a moment, is that $\sin (x)$ can be written as an " infinite polynomial" in the following way:

$\begin{equation} \label{eq:taylorsin} \sin (x) = x - \frac{x^3}{3!} +\frac{x^5}{5!} -\frac{x^7}{7!} + \cdots + (-1)^{k}\frac{x^{2k+1}}{(2k+1)!} + \cdots \end{equation}$

(20)

This is called a power series for $\sin (x)$ because it is a series in terms of powers of $x$ . You may be aware that you can approximate $\sin (x) \approx x$ when $x$ is small. This just uses the first term in the series above. You can get better approximations to $\sin (x)$ as

$\begin{equation} \sin (x) \approx x - \frac{x^3}{3!} \end{equation}$

(21)

and

$\begin{equation} \sin (x) \approx x - \frac{x^3}{3!} +\frac{x^5}{5!} \end{equation}$

(22)

by taking successive terms. Most other functions, such as $\cos (x), e^ x, \ln (x),$ etc. have power series. It is series such as these that your pocket calculator uses to calculate numerical values. In formula (20) $x$ is in radians not degrees and it would not be nearly so beautiful if $x$ was an angle in degrees. In fact, one of the reasons we choose to use radians is because this allows us to write the formula in this way.

Euler's solution to the Basel Problem

Leonhard Euler

Euler was working on the Basel Problem at the age of 24 in 1731 by calculating a numerical approximation. This is an arduous task by hand with a series which converges as slowly as this. In 1735 he arrived at the following exact result:

$\begin{equation} \sum _{k=1}^\infty \frac{1}{k^2} = \frac{\pi ^2}{6}. \end{equation}$

(23)

This is a truly remarkable result. No one expected the value $\pi$ , the ratio of the circumference of a circle to the diameter, to appear in the formula for the sum. Euler starts with an $n$ th degree polynomial $p(x)$ with the following properties:

$p(x)$ has non-zero roots $a_1,\cdots ,a_ n$ ,
$p(0)=1$ .

Then $p(x)$ may be written as a product in the following form:

$\begin{equation} p(x) = \left(1-\frac{x}{a_1}\right) \left(1-\frac{x}{a_2}\right) \cdots \left(1-\frac{x}{a_ n}\right). \end{equation}$

(24)

We paraphrase Euler’s next claim as "what holds for a finite polynomial holds for an infinite polynomial". He applies this claim to the polynomial

$\begin{equation} p(x) =1 - \frac{x^2}{3!} +\frac{x^4}{5!} -\frac{x^6}{7!} + \cdots \end{equation}$

(25)

which is an infinite polynomial with $p(0)=1$ . Furthermore, as Euler knew, $\sin (x)$ can be written as a series:

$\begin{equation} \sin (x) = x - \frac{x^3}{3!} +\frac{x^5}{5!} -\frac{x^7}{7!} + \cdots + (-1)^{k}\frac{x^{2k+1}}{(2k+1)!} + \cdots \end{equation}$

(26)

Multiplying $p(x)$ by $x$ he obtained

$\begin{equation} x p(x) = x - \frac{x^3}{3!} +\frac{x^5}{5!} -\frac{x^7}{7!} + \cdots = \sin (x). \end{equation}$

(27)

This has zeros at $x=\pm k\pi$ for $k=1,2,\cdots$ since these are the zeros of $\sin (x)$ . We can now use the claim above and write $p(x)$ as an infinite product and equate the two as

$\displaystyle$	$\displaystyle$	$\displaystyle 1 - \frac{x^2}{3!} +\frac{x^4}{5!} -\frac{x^6}{7!} + \cdots = p(x)$	(28)
$\displaystyle$	$\displaystyle =$	$\displaystyle \left(1-\frac{x}{\pi }\right) \left(1+\frac{x}{\pi }\right) \left(1-\frac{x}{2\pi }\right) \left(1+\frac{x}{2\pi }\right) \times \cdots$	(29)
$\displaystyle$	$\displaystyle =$	$\displaystyle \left[1-\frac{x^2}{\pi ^2}\right] \left[1-\frac{x^2}{4\pi ^2}\right] \left[1-\frac{x^2}{9\pi ^2}\right] \times \cdots$	(30)

The second line pairs the positive and negative roots – the last line uses the difference of two squares to combine these. If you don’t believe this can be done you are right to question the logic here! Euler is being incredibly bold in his assertion that "what holds for a finite polynomial holds for an infinite polynomial". His use turns out to give the correct answer in this case!

Euler’s trick is to write $p(x)$ in two different ways. He exploits this by expanding the right hand side. This infinite product will be very complicated but there will be a constant term $1$ and one can collect the $x^2$ term without too much effort as follows:

$\begin{equation} 1 - \frac{x^2}{3!} +\frac{x^4}{5!} -\frac{x^6}{7!} + \cdots = 1 - \left( \frac{1}{\pi ^2} + \frac{1}{4\pi ^2} + \frac{1}{9\pi ^2} + \frac{1}{16\pi ^2} + \cdots \right)x^2 + \cdots \end{equation}$

(31)

Now Euler equates the coefficients of $x^2$ to conclude that

$\begin{equation} -\frac{1}{3!} =- \left( \frac{1}{\pi ^2} + \frac{1}{4\pi ^2} + \frac{1}{9\pi ^2} + \frac{1}{16\pi ^2} + \cdots \right), \end{equation}$

(32)

which gives

$\begin{equation} 1 +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} + \cdots = \frac{\pi ^2}{6}. \end{equation}$

(33)

Now Euler didn’t stop here – he expanded the product further and equated other coefficients to sum other series. In this way he obtained

$\begin{equation} \sum _{k=1}^\infty \frac{1}{k^4} = \frac{\pi ^4}{90} \quad \mbox{and} \quad \sum _{k=1}^\infty \frac{1}{k^6} = \frac{\pi ^6}{945}. \end{equation}$

(34)

In 1744 he obtained

$\begin{equation} \sum _{k=1}^\infty \frac{1}{k^{26}} = \frac{2^{24} 76977927 \pi ^{26}}{27!} \end{equation}$

(35)

by this method. In principle his method solves

$\begin{equation} \sum _{k=1}^\infty \frac{1}{k^{2n}} \end{equation}$

(36)

for all natural numbers $n$ .

Extensions of the Basel problem

In a style typical of Euler, he not only solved the problem in hand but also used the method to solve a class of related problems. You will notice that his method only works for even powers. What then, about

$\begin{equation} \sum _{k=1}^\infty \frac{1}{k^3}? \end{equation}$

(37)

The answer is: we don’t know. This is still an open problem, and quite a famous one. Euler tried to solve it of course, but failed. The best he could do was

$\begin{equation} \sum _{k=0}^\infty \frac{(-1)^ k}{(2k+1)^3} = 1 - \frac{1}{27} + \frac{1}{125} - \cdots = \frac{\pi ^3}{32}. \end{equation}$

(38)

About the author

Chris Sangwin is a member of staff in the School of Mathematics and Statistics at the University of Birmingham. He is a Research Fellow in the Learning and Teaching Support Network centre for Mathematics, Statistics, and Operational Research. His interests lie in mathematical Control Theory.