

Anyone can uncover the mystery
The number 6174 is a really mysterious number. At first glance, it might not seem so obvious. But as we are about to see, anyone who can subtract can uncover the mystery that makes 6174 so special.
Kaprekar's operation
In 1949 the mathematician D. R. Kaprekar from Devlali, India, devised a process now known as Kaprekar's operation. First choose a four digit number where the digits are not all the same (that is not 1111, 2222,...). Then rearrange the digits to get the largest and smallest numbers these digits can make. Finally, subtract the smallest number from the largest to get a new number, and carry on repeating the operation for each new number.
It is a simple operation, but Kaprekar discovered it led to a surprising result. Let's try it out, starting with the number 2005, the digits of last year. The maximum number we can make with these digits is 5200, and the minimum is 0025 or 25 (if one or more of the digits is zero, embed these in the left hand side of the minimum number). The subtractions are:
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
When we reach 6174 the operation repeats itself, returning 6174 every time. We call the number 6174 a kernel of this operation. So 6174 is a kernel for Kaprekar's operation, but is this as special as 6174 gets? Well not only is 6174 the only kernel for the operation, it also has one more surprise up its sleeve. Let's try again starting with a different number, say 1789.
9871 - 1789 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
We reached 6174 again!

A very mysterious number...
When we started with 2005 the process reached 6174 in seven steps, and for 1789 in three steps. In fact, you reach 6174 for all four digit numbers that don't have all the digits the same. It's marvellous, isn't it? Kaprekar's operation is so simple but uncovers such an interesting result. And this will become even more intriguing when we think about the reason why all four digit numbers reach this mysterious number 6174.
Only 6174?
The digits of any four digit number can be arranged into a maximum number by putting the digits in descending order, and a minimum number by putting them in ascending order. So for four digits a,b,c,d where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0
and a, b, c, d are not all the same digit, the maximum number is abcd and the minimum is dcba.
We can calculate the result of Kaprekar's operation using the standard method of subtraction applied to each column of this problem:
| a | b | c | d | |
| - | d | c | b | a |
|
|
||||
|---|---|---|---|---|
| A | B | C | D | |
which gives the relations
| D = 10 + d - a (as a > d) |
| C = 10 + c - 1 - b = 9 + c - b (as b > c - 1) |
| B = b - 1 - c (as b > c) |
| A = a - d |
for those numbers where a>b>c>d.
A number will be repeated under Kaprekar's operation if the resulting number ABCD can be written using the initial four digits a,b,c and d. So we can find the kernels of Kaprekar's operation by considering all the possible combinations of {a, b, c, d} and checking if they satisfy the relations above. Each of the 4! = 24 combinations gives a system of four simultaneous equations with four unknowns, so we should be able to solve this system for a, b, c and d.
It turns out that only one of these combinations has integer solutions that satisfy 9 ≥ a ≥ b ≥ c ≥ d ≥ 0. That combination is ABCD = bdac, and the solution to the simultaneous equations is a=7, b=6, c=4 and d=1. That is ABCD = 6174. There are no valid solutions to the simultaneous equations resulting from some of the digits in {a,b,c,d} being equal. Therefore the number 6174 is the only number unchanged by Kaprekar's operation — our mysterious number is unique.
For three digit numbers the same phenomenon occurs. For example applying Kaprekar's operation to the three digit number 753 gives the following:
753 - 357 = 396
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
The number 495 is the unique kernel for the operation on three digit numbers, and all three digit numbers reach 495 using the operation. Why don't you check it yourself?
How fast to 6174?
It was about 1975 when I first heard about the number 6174 from a friend, and I was very impressed at the time. I thought that it would be easy to prove why this phenomenon occurred but I could not actually find the reason why. I used a computer to check whether all four digit numbers reached the kernel 6174 in a limited number of steps. The program, which was about 50 statements in Visual Basic, checked all of 8991 four digit numbers from 1000 to 9999 where the digits were not all the same.
The table below shows the results: every four digit number where the digits aren't all equal reaches 6174 under Kaprekar's process, and in at most seven steps. If you do not reach 6174 after using Kaprekar's operation seven times, then you have made a mistake in your calculations and should try it again!
| Iteration | Frequency |
|---|---|
| 0 | 1 |
| 1 | 356 |
| 2 | 519 |
| 3 | 2124 |
| 4 | 1124 |
| 5 | 1379 |
| 6 | 1508 |
| 7 | 1980 |
Which way to 6174?
My computer program checked all 8991 numbers, but in his article Malcolm Lines explains that it is enough to check only 30 of all the possible four digit numbers when investigating Kaprekar's operation.
As before let's suppose that the four digit number is abcd, where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0.
Let us calculate the first subtraction in the process. The maximum number is 1000a+100b+10c+d and the minimum number is 1000d+100c+10b+a. So the subtraction is:
1000a + 100b + 10c + d - (1000d + 100c + 10b + a)
= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a)
= 999(a-d) + 90(b-c)
The possible value of (a-d) is from 1 to 9, and (b-c) is from 0 to 9. By running through all the possibilities, we can see all the possible results from the first subtraction in the process. These are shown in Table 1.
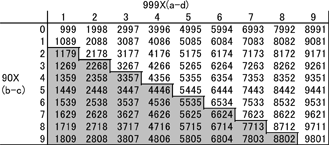
Table 1: Numbers after the first subtraction in Kaprekar's process
We are only interested in numbers where the digits are not all equal and
a ≥ b ≥ c ≥ d,
therefore we only need to consider those where (a-d) ≥ (b-c). So we can ignore the grey region in Table 1 which contains those numbers where
(a-d) < (b-c).
Now we arrange the digits of the numbers in the table in descending order, to get the maximum number ready for the second subtraction:
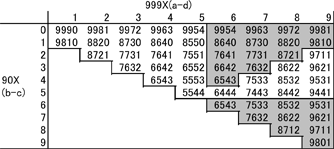
Table 2: Maximum numbers, ready for the second subtraction
We can ignore the duplicates in Table 2 (the grey regions), and are left with just 30 numbers to follow through the rest of the process. The following figure shows the routes which these numbers take to reach 6174.
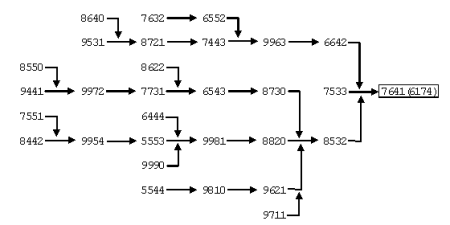
How these 30 numbers reach 6174
From this figure you can see how all the four digit numbers reach 6174 and reach it in at most seven steps. Even so I still think it is very mysterious. I guess Kaprekar, who discovered this number, was extremely clever or had a lot of time to think about it!
Two digits, five digits, six and beyond...
We have seen that four and three digit numbers reach a unique kernel, but how about other numbers? It turns out that the answers for those is not quite as impressive. Let try it out for a two digit number, say 28:
82 - 28 = 54
54 - 45 = 9
90 - 09 = 81
81 - 18 = 63
63 - 36 = 27
72 - 27 = 45
54 - 45 = 9
It doesn't take long to check that all two digit numbers will reach the loop 9→81→63→27→45→9. Unlike for three and four digit numbers, there is no unique kernel for two digit numbers.
But what about five digits? Is there a kernel for five digit numbers like 6174 and 495? To answer this we would need to use a similar process as before: check the 120 combinations of {a,b,c,d,e} for ABCDE such that
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
and
abcde - edcba = ABCDE.
Thankfully the calculations have already been done by a computer, and it is known that there is no kernel for Kaprekar's operation on five digit numbers. But all five digit numbers do reach one of the following three loops:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994
As Malcolm Lines points out in his article, it will take a lot of time to check what happens for six or more digits, and this work becomes extremely dull! To save you from this fate, the following table shows the kernels for two digit to ten digit numbers (for more see Mathews Archive of Recreational Mathematics). It appears that Kaprekar's operation takes every number to a unique kernel only for three and four digit numbers.
| Digits | Kernel |
|---|---|
| 2 | None |
| 3 | 495 |
| 4 | 6174 |
| 5 | None |
| 6 | 549945, 631764 |
| 7 | None |
| 8 | 63317664, 97508421 |
| 9 | 554999445, 864197532 |
| 10 | 6333176664, 9753086421, 9975084201 |
Beautiful, but is it special?
We have seen that all three digit numbers reach 495, and all four digit numbers reach 6174 under Kaprekar's operation. But I have not explained why all such numbers reach a unique kernel. Is this phenomenon incidental, or is there some deeper mathematical reason why this happens? Beautiful and mysterious as the result is, it might just be incidental.
Let's stop and consider a beautiful puzzle by Yukio Yamamoto in Japan.
If you multiply two five digit numbers you can get the answer 123456789. Can you guess the two five digit numbers?
This is a very beautiful puzzle and you might think that a big mathematical theory should be hidden behind it. But in fact it's beauty is only incidental, there are other very similar, but not so beautiful, examples. Such as:
(We can give you a hint to help you solve these puzzles, and here are the answers.)
If I showed you Yamamoto's puzzle you would be inspired to solve it because it is so beautiful, but if I showed you the second puzzle you might not be interested at all. I think Kaprekar's problem is like Yamamoto's number guessing puzzle. We are drawn to both because they are so beautiful. And because they are so beautiful we feel there must be something more to them when in fact their beauty may just be incidental. Such misunderstandings have led to developments in mathematics and science in the past.
Is it enough to know all four digit numbers reach 6174 by Kaprekar's operation, but not know the reason why? So far, nobody has been able to say that all numbers reaching a unique kernel for three and four digit numbers is an incidental phenomenon. This property seems so surprising it leads us to expect that a big theorem in number theory hides behind it. If we can answer this question we could find this is just a beautiful misunderstanding, but we hope not.
Note from the editors: many readers noticed that repeatedly adding up the digits of any of the kernels of Kaprekar's operation always equals 9. Find out why in this follow-up to the article.
References
- Kaprekar, D. R., "Another Solitaire Game", Scripta Mathematica, vol 15, pp 244-245 (1949)
- Gardner, Martin, "The Magic Numbers of Doctor Matrix", Japanese version, Tokyo: Kinokuniya (1978)
- Lines, Malcolm E., A number for your thoughts: facts and speculations about numbers..., Bristol: Hilger (1986)
- Nishiyama, Yutaka, Kurashi no Algorithm, Kyoto: Nakanishiya (1993)
About the author

Yutaka Nishiyama is a professor at Osaka University of Economics, Japan. After studying mathematics at the University of Kyoto he went on to work for IBM Japan for 14 years. He is interested in the mathematics that occurs in daily life, and has written seven books about the subject. The most recent one, called "The mystery of five in nature", investigates, amongst other things, why many flowers have five petals. Professor Nishiyama is currently visiting the University of Cambridge.