
On the 25th of May 1997 an unmanned cargo ship named Progress crashed into the Russian space station Mir, tearing a hole into Mir's side and sending it hurtling through space. In his desperate attempt to save Mir and its crew, NASA astronaut Michael Foale had no choice but to get right down to the maths that governs space flight.
Crunch
The space station Mir, manned by NASA astronaut and scientist Michael Foale, Flight Engineer Alexander "Sasha" Lazutkin and Commander Vasily Tsibliev, had been put in orbit around Earth to test for the first time the feasibility of long-term human habitation in space. On this particular day in May 1997, the unmanned cargo ship Progress, orbiting Earth a few kilometres away from the station, was due to dock with Mir, under remote-control by Mir's crew.

The space station Mir. Image courtesy NASA.
But this wasn't a routine docking manoeuvre. "What was so different and dangerous about that particular day," says Michael Foale, "was that we had been given orders to disconnect the antennae systems on the Progress, so that the Progress did not know how fast it was coming into the space station or how far away it was. All we had was a view from a camera, mounted on the Progress, coming in towards Mir. This amounted to flying a cargo rocket weighing seven tons, with very, very weak thrusters, and a two-second time delay between inputting commands at the controls and the Progress's reaction.
"Why were we taking this risk? At the time, the cash situation of the Russian space programme was very critical. The equipment controlling the automatic guidance systems that would allow the two space vehicles to come together was produced in the Ukraine, which, after the split of the Soviet Union, was no longer linked to Russia. The Ukrainians demanded a lot of money for this equipment, so Russia wanted to see if we could do all this manually."

Michael Foale with a model of Mir. Image © Mathematical Sciences Research Institute.
If you imagine guiding a seven ton truck into a narrow parking slot by remote control, only with the help of a small black-and-white monitor and subject to a time delay, you get some idea of the difficult task that was facing Vasily Tsibliev, who was to execute the docking manoeuvre. But there was another complication: viewing the world from the Mir was very different to viewing it from the Progress.
To understand this, think of a plane starting from London and aiming straight at Perth in Australia. If the plane was to roll over the surface of the Earth along the straight line between London and Perth, it would eventually arrive. As soon as it takes to the air, however, it leaves the Earth's frame of reference. While it is flying into the prescribed direction, the Earth underneath it rotates, causing the plane to miss its target. From the point of view of someone on Earth, the plane has flown along a curve, as if it had been diverted from its original path by some external force. This fictitious force — fictitious because it is only a result of our viewpoint — is called the Coriolis force.
The same difficulty applies in space: sitting within a space station you are in what is called a rotating frame of reference. Any space vehicle thrusting towards you is not part of this frame of reference and will feel the Coriolis force. You have to take account of this force when guiding the vehicle — or miss your target.
"Vasily had not been trained on this. This was a poorly planned experiment, one which was going to affect our safety quite critically," says Michael. The Progress was moving in at about six metres per second, meaning that Vasily could not really ascertain its speed until the very end. "It all happens in the last few seconds," says Michael, "then suddenly the angles open up and the speed of the Progress becomes apparent. But when your thrusters are very small, as they are on the Progress, then you need to brake for a long time to take away your speed. Vasily's recognition of the Progress's speed came too late."
Sasha Lozutkin, who had seen through one of Mir's windows that disaster was imminent, had time to shout out a warning — and then the Progress crunched straight into Mir's side.
"I didn't feel the crunch because I was not touching anything, but I could see our equipment shake and hear a big bang," says Michael. "That's when I thought 'this could be the moment we all die'. The de-pressurisation alarm went off and this meant that there really was a hole in the station. I felt the pressure fall in my ears. I started heading for the Soyuz, Mir's only life boat."

The space station Mir. Five modules attach to a central node. The life boat Soyuz is the small cone shaped object protruding from the central node and pointing towards the top left-hand corner. Image courtesy NASA.
But meanwhile Sasha, who had seen the impact, had other plans. The Mir is made up of a central node to which five different modules attach by hatchways. The Progress had hit one of these modules, rather than the central node, and so Sasha had decided to simply close off the damaged module. As precious minutes and air were trickling away, the crew set about cutting eighteen thick cables which were preventing them from closing the door to the damaged module. Sparks flying, the last cable finally gave in and the hatchway's door could be lifted into position. "I could immediately hear the door being sucked into place," says Michael "and about a minute later I could feel the pressure stabilise. At this point the emergency was over."
Silence
The emergency was over, but Mir and its crew were far from safe. What they had just done was disconnect thirty per cent of the station's power supply, which came from the solar arrays attached to the damaged module. "Within twenty to thirty minutes after the collision, every single piece of equipment on the station went dead," says Michael. "It was a completely silent station. It's quite eerie to be in a station in space where there is no sound except for your own breathing. And then it started to get cold. Really, really cold."
There still were functional solar arrays attached to the undamaged modules, and with some exposure to the Sun, these arrays could provide sufficient power to keep operations going. But exposure to the Sun was precisely the problem. Before the impact, Mir had been orbiting Earth all the while maintaining the same attitude towards the Sun. Its solar panels had been facing straight into the Sun, slowly turning to keep track whenever Mir moved over the Earth's sunny side. But Progess's impact had knocked Mir out of its attitude to the Sun. Worse, it had also set it spinning about its own centre of gravity at a rate too fast for the solar arrays to keep up.
There was only one way to save the station: the lifeboat called Soyuz, still attached to the station, had its own power and thrusters. Using these thrusters it might be possible to counteract Mir's tumble and to manoeuvre it into a position that allowed its solar arrays to find the Sun. A risky plan, as Michael explains: "Remember, this is our life boat. It carries the fuel to take us back to Earth. We couldn't afford to use our fuel up. But at the same time, we had no communications with the ground, because the station was dead, and we didn't seem to be getting into a better situation. We had already gone a few orbits without power. So in the end the three of us agreed to give it a go."

Some of the damage done to Mir. Image courtesy NASA.
Rule of thumb
The initial attempts to halt Mir's bad spin were a trial-and-error affair involving much shouting of commands and floating about the station. Without communications with the ground, the only way to ascertain how Mir was spinning was, quite literally, by rule of thumb: "I knew that the Moon was about half a degree in angular width. My thumb covered the Moon about three times, making one and a half degrees." Stretching his thumb out against the stars and watching the stars drifting past it, Michael managed to get a rough idea of the rate and direction of Mir's spin.
Based on his thumb measurements, Michael shouted instructions to Vasily who was controlling the Soyuz's thrusters. After four and a half hours and some nerve-wrecking failed attempts, they finally saw a result. The Mir's spin slowed and the station's position became relatively stable with respect to the Sun.

The life boat Soyuz, about to attach to Mir. Image courtesy NASA.
But this wasn't the end of the problem. For a space station to keep facing the Sun in more or less the same way while it orbits Earth, powerful control mechanisms are needed. Once the power is down, these mechanisms stop functioning. The minutest tugs and pulls will cause the station to start drifting again and over the course of just a few hours it will lose its stable attitude toward the Sun — unless you put the right spin on it.
The maths behind the spin
As you can see in the image above, the space station Mir is quite a symmetrical object. It is set out along three axes, each perpendicular to the other two, with its centre of gravity located roughly at its central node. The crucial component of Mir's movement was not its orbit around Earth, but the way it revolved about its own centre of gravity, as this was making it hard for the solar arrays to pick up energy. So for simplicity, imagine, for the moment, this centre of gravity being fixed in one place.
The Swiss mathematician Leonhard Euler showed in the 18th century that any movement of a rigid body that keeps one of its points fixed must be a rotation about an axis going through the fixed point. In other words, when Mir was set spinning, its initial movement was a rotation about an axis passing through its centre of gravity. However, in general such a rotation is not stable: as the object spins about one axis, it may start rotating about other axes too. In Mir's case, this meant that a spin about an arbitrary axis afforded practically no chance of a stable attitude toward the Sun.
Euler's equations of rotational motion describe exactly how the movement of a rotating body evolves over time, and capture how this movement changes if you apply certain external forces. His equations show that every body possesses three very special axes, and that the body's movement is crucially determined by three numbers called the principal moments of inertia.
Euler's equations of motion
Here, I1, I2 and I3 are the principal moments of inertia. The ω1, ω2 and ω3 are functions of time and together describe the motion the body has performed after time t. There are similar equations describing the motion when external force, or torque, is applied.
When you set an object spinning about an axis, you need to apply a certain amount of force to get it going in the first place. This amount depends on the way in which the object's mass is distributed with respect to the axis: a wheel, for example, is harder to spin when most of its mass is located around its rim, than when it is concentrated close to the centre. Mathematicians use a number to measure the resistance of the object to being spun, and this number is called a moment of inertia. Each axis has its own moment of inertia.
Euler noticed that, no matter which object you are spinning, whether it's a space station, a potato or an elephant, the same basic pattern always occurs. The axis that gives you the smallest moment of inertia (the least resistance to being spun) is perpendicular to the axis giving you the greatest moment of inertia. These two axes, together with the line that is perpendicular to both of them, are known as the object's principal axes of inertia.
When an object has some symmetry, the principal axes often coincide with the symmetry axes, and this is the case for Mir: its principal axes of inertia are exactly the x, y and z-axes shown in the image below. What Euler's equations also show — and what Michael Foale knew — is that the two axes associated to the smallest and the largest moment of inertia give rise to stable rotations: spin Mir around one of these axes and it will keep on spinning nicely in the same direction. A spin about the third axis, however, is not stable.

Mir's principal axes. Image courtesy NASA.
The right spin
A spin around one of Mir's stable axes could be Mir's saviour, but it could also spell doom. If the axis was oriented so that the solar arrays face into the Sun whenever Mir passes on the Earth's sunny side, then a stable spin would allow it to recharge its battery continually. If, however, the axis was oriented so that the solar arrays can't ever pick up the Sun, then the station would be lost: a lot of energy would be required to brake out of the stable spin and energy was precisely what Mir didn't have. Mir would be locked into the bad spin forever and, as Michael says, "that would be it, we would have to abandon the station."
So which of Mir's principal axes were stable? Unfortunately, Michael and his colleagues did not know. Neither did ground control in Moscow, as it turned out later. Using a cracked and broken model of the Mir, and supplementing it with torches taped to its ends, Michael eventually ascertained that their best bet lay with the y-axis. The Soyuz's thrusters, because of their position, were unable to induce a rotation about the x-axis, and rotation about the z-axis would not have allowed the functioning solar arrays to pick up the Sun. "The best thing we could do was to rotate about the y-axis and hope that it was stable.
Moments of inertia and stable spins
To demonstrate how a body spins about its three principal axes, take a box-shaped object, for example an empty cereal box. Its three principal axes are the ones shown in the figure below.
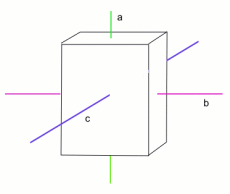
If you throw the box up in the air giving it a spin about the axis marked a in the figure, you will find that the box keeps spinning in that direction until it falls to the floor. The same happens if you give it a spin about the axis marked c. These two axes have the smallest and largest moment of inertia and they are stable.
But if you give the box a spin about the axis marked b, then the box will do a wobble and a flip in mid-air. This axis has the middle moment of inertia — it is unstable.
"Eventually, we managed to get a rough spin about the y-axis and to orient it in what we thought was the direction of the Sun. We could not know for sure because at the time we were passing the dark side of the Earth. But then we saw the rim of the Earth go blue, then red, and then the Sun popped out — and low and behold it was roughly in the direction of the y-axis."
Almost safe
"At that point we managed to charge the station's batteries continually while the Mir passed on the Earth's sunny side, which takes about an hour. That was enough to bring the station back to life and to bring up communications with the ground. With Moscow's help we could get accurate control of our orientation. After 30 hours we could finally relax, get some sleep and start dealing with other consequence of the collision."
The y-axis, as it turned out, was not stable. "I noticed that our rotation was stable for only about one and a half hours. Then the Mir would do a flip and the solar arrays were pointing exactly in the opposite direction. What we had discovered was that the y-axis was the one with the middle moment of inertia." Luckily though, with batteries charged and communications to the ground re-established, this did not turn out to be a major problem.

Michael Foale on a space walk to repair the Hubble Space Telescope in 1999. Image courtesy NASA.
But still, Michael's adventure was far from over. After the accident, he remained on Mir for another three and a half months until a space shuttle came to get him in October. "After the initial emergency, we lost control again two or three times, because in rescuing Mir we had made its control systems very vulnerable. During this time my worst fear was that we would somehow get locked into a bad spin about the z-axis, which wouldn't allow us to recharge our batteries." So, using a laptop with shaky batteries, Michael set about trying to solve Euler's equations once and for all to get an accurate idea of the Mir's rotation dynamics. He never quite finished until he got back to Earth, where he finally published is work. If you are ready to brave the equations, you can read his paper in The Mathematica Journal. The paper includes a computer model of the rotating Mir, which Michael created using the program Mathematica.
This whole incident holds many lessons for space craft design. But the clearest message is one that rarely gets mentioned: it's the important role of maths. "Mathematics is everywhere in space flight," says Michael. "When I think about a space craft in orbit, I always think in terms of the underlying maths and physics. I didn't suddenly turn on my ability to think about maths when the accident happened; it was a continuation of my usual, mathematical way of thinking. You cannot be an effective mission designer, astronaut, flight controller or engineer if you don't know maths."
About this article
This article is based on the DVD The right spin, written and narrated by Robert Osserman and produced by the Clay Mathematics Institute and the Mathematical Sciences Research Institute.
Michael Foale studied at the University of Cambridge, Queens College. He received a bachelor of arts in Physics, Natural Science Tripos, with 1st class honours, and completed his doctorate in Laboratory Astrophysics at Cambridge in 1982. He was selected as an astronaut candidate by NASA in 1987. He was on the first space shuttle flight to rendezvous with Mir, and returned in 1997 for a 4-month stay aboard Mir. In 1999 he engaged in a space walk as part of the mission to repair and upgrade the Hubble Space Telescope. Michael Foale currently holds the U.S. record for time spent in space, having spent over a year of his life away from Earth.

Marianne Freiberger is co-editor of Plus.